2024-2025学年上学期初中数学人教版八年级期末必刷常考题之乘法公式练习

这是一份2024-2025学年上学期初中数学人教版八年级期末必刷常考题之乘法公式练习，共15页。试卷主要包含了已知a﹣b＝6，ab＝﹣7，阅读理解，已知，计算，＝ 　 　等内容，欢迎下载使用。
1．（2024春•娄星区校级期中）已知a﹣b＝6，ab＝﹣7．求：
（1）a2+b2的值；
（2）（a+b）2+2（a﹣b）2的值．
2．（2024秋•香坊区校级期中）如图，某市有一块长为（3a+b）米，宽为（2a+b）米的长方形地块，规划部门计划在中间留一块边长为（a+b）米的正方形空地修建雕像，其余部分铺设草坪（阴影部分）．
（1）求草坪的面积是多少平方米？（用含a、b的代数式表示）
（2）若a、b满足（x+2）（x+3）＝x2+ax+b时，草坪的单价为每平方米50元．求购买草坪所需要的总费用．
3．（2024秋•浦东新区期中）计算：（2x﹣3y）（3x+2y）﹣（2x﹣y）（y+2x）．
4．（2024秋•普陀区期中）阅读理解．
已知（a﹣12）2+（14﹣a）2＝6，求（a﹣13）2的值．
解：由（a﹣12）2+（14﹣a）2＝6，可得[（a﹣13）+1]2+[（a﹣13）﹣1]2＝6．
整理得（a﹣13）2+2（a﹣13）+1+（a﹣13）2﹣2（a﹣13）+1＝6．
2（a﹣13）2+2＝6
得（a﹣13）2＝2．
请仿照上述方法，完成下列问题：
（1）已知（a﹣98）2+（96﹣a）2＝10，求（a﹣97）2的值．
（2）已知（a﹣2024）2＝8，求（a﹣2025）2+（2023﹣a）2的值．
5．（2023秋•宜宾期末）如图①是一个长为2a、宽为2b的长方形，沿图中虚线用剪刀均分成四块小长方形，然后按图②的形状拼成一个正方形．
（1）观察图②．请你直接写出下列三个式子：（a+b）2、（a﹣b）2、ab之间的等量关系式为 ；
（2）若m、n均为实数，且m+n＝3，mn＝﹣4，且m＜n，运用（1）所得到的公式求m﹣n的值；
（3）如图③，S1、S2分别表示边长为x、y的正方形的面积，且A、B、C三点在一条直线上，若S1+S2＝20，S△BCD+S△ACF＝8，求图中两个正方形的周长之和．
二．填空题（共5小题）
6．（2024春•惠山区期中）如果x2+mx+16完全平方式，则m的值等于 ．
7．（2024秋•南岗区校级期中）已知：a+b＝3，ab＝5，则a2+b2﹣2a﹣2b+6＝ ．
8．（2024秋•金牛区校级期中）如图，已知边长为a，b的长方形，若它的周长为20，面积为32，则a2+b2的值为 ．
9．（2024秋•江汉区期中）计算：10012﹣1006×994＝ ．
10．（2024秋•黄浦区期中）计算：（2x﹣5y）（2x+5y）＝ ．
三．选择题（共5小题）
11．（2024秋•东城区校级期中）若a+b＝3，ab＝﹣12，则a2﹣ab+b2的值为（ ）
A．57B．21C．45D．33
12．（2024秋•黄浦区期中）下列各式能用平方差公式计算的是（ ）
A．（a﹣b）（b﹣a）B．（a+b）（b+a）
C．（a﹣b）（﹣a﹣b）D．（a+b）（﹣a﹣b）
13．（2024秋•金牛区校级期中）若a﹣b＝8，a2+b2＝82，则2ab的值为（ ）
A．9B．﹣9C．18D．﹣18
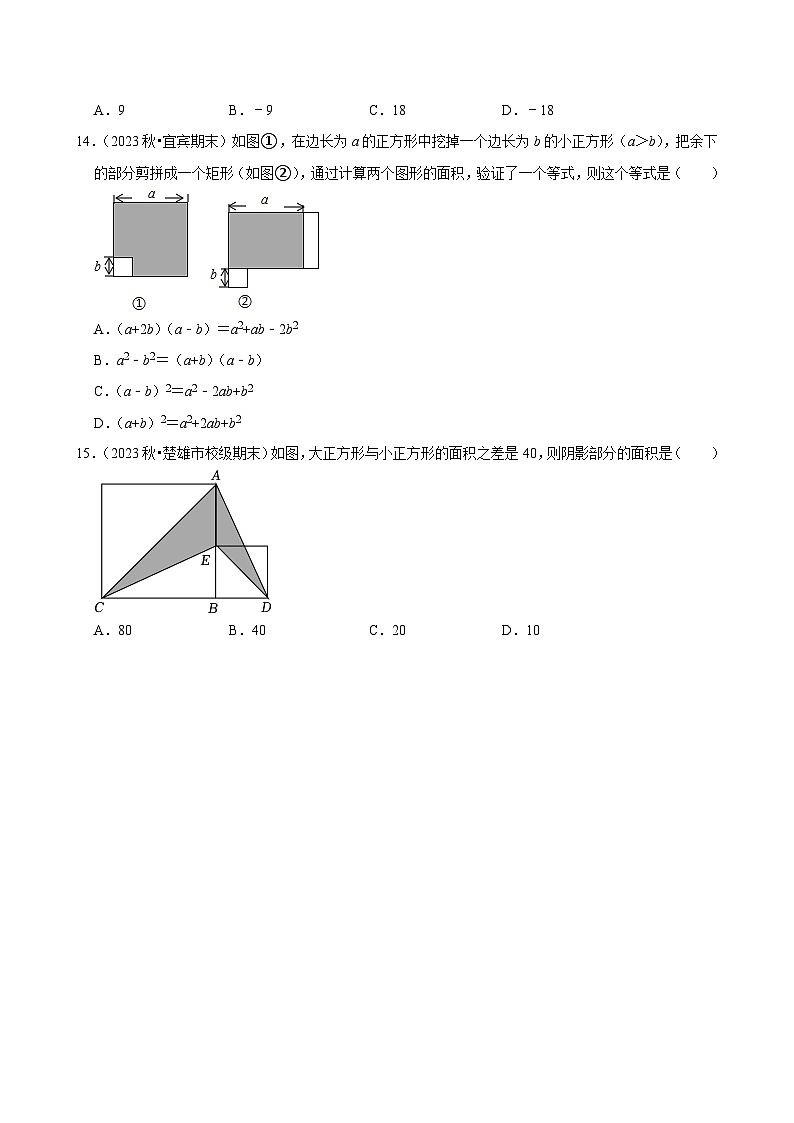
14．（2023秋•宜宾期末）如图①，在边长为a的正方形中挖掉一个边长为b的小正方形（a＞b），把余下的部分剪拼成一个矩形（如图②），通过计算两个图形的面积，验证了一个等式，则这个等式是（ ）
A．（a+2b）（a﹣b）＝a2+ab﹣2b2
B．a2﹣b2＝（a+b）（a﹣b）
C．（a﹣b）2＝a2﹣2ab+b2
D．（a+b）2＝a2+2ab+b2
15．（2023秋•楚雄市校级期末）如图，大正方形与小正方形的面积之差是40，则阴影部分的面积是（ ）
A．80B．40C．20D．10
2024-2025学年上学期初中数学人教版八年级期末必刷常考题之乘法公式
参考答案与试题解析
一．解答题（共5小题）
1．（2024春•娄星区校级期中）已知a﹣b＝6，ab＝﹣7．求：
（1）a2+b2的值；
（2）（a+b）2+2（a﹣b）2的值．
【考点】完全平方公式．
【专题】整式；运算能力．
【答案】见试题解答内容
【分析】（1）由（a﹣b）2＝a2﹣2ab+b2，给等式两边同时加2ab，根据已知条件即可得出答案；
（2）由（a﹣b）2＝a2﹣2ab+b2，给等式两边同时加4ab，右边为a2+2ab+b2，即（a+b）2，根据已知条件即可得出答案．
【解答】解：（1）∵a﹣b＝6，ab＝﹣7，
∴a2+b2＝（a﹣b）2+2ab＝62+2×（﹣7）＝22；
（2）∵（a+b）2＝（a﹣b）2+4ab，a﹣b＝6，ab＝﹣7，
∴（a+b）2＝62+4×（﹣7）＝8，
∴（a+b）2+2（a﹣b）2＝8+2×62＝80．
【点评】本题主要考查了完全平方公式的变式应用，熟练应用完全平方公式的变式进行计算是解决本题的关键．
2．（2024秋•香坊区校级期中）如图，某市有一块长为（3a+b）米，宽为（2a+b）米的长方形地块，规划部门计划在中间留一块边长为（a+b）米的正方形空地修建雕像，其余部分铺设草坪（阴影部分）．
（1）求草坪的面积是多少平方米？（用含a、b的代数式表示）
（2）若a、b满足（x+2）（x+3）＝x2+ax+b时，草坪的单价为每平方米50元．求购买草坪所需要的总费用．
【考点】完全平方公式的几何背景；多项式乘多项式．
【专题】整式；运算能力．
【答案】（1）（5a2+3ab）平方米；
（2）10750元．
【分析】（1）根据图形中面积之间的关系进行计算即可；
（2）求出a、b的值，代入求出草坪的面积，再根据单价×数量＝总价进行计算即可．
【解答】解：（1）S阴影部分＝S长方形﹣S正方形
＝（3a+b）（2a+b）﹣（a+b）2
＝6a2+3ab+2ab+b2﹣a2﹣2ab﹣b2
＝（5a2+3ab）平方米；
（2）∵（x+2）（x+3）＝x2+5x+6＝x2+ax+b，
∴a＝5，b＝6，
∴草坪的面积为5×52+3×5×6＝215（平方米），
∴购买草坪所需要的总费用为215×50＝10750（元）．
【点评】本题考查多项式乘多项式，完全平方公式以及代数式求值，掌握多项式乘多项式的计算方法，完全平方公式的结构特征是正确解答的关键．
3．（2024秋•浦东新区期中）计算：（2x﹣3y）（3x+2y）﹣（2x﹣y）（y+2x）．
【考点】平方差公式；多项式乘多项式．
【专题】整式；运算能力．
【答案】2x2﹣5xy﹣5y2．
【分析】先根据平方差公式和多项式乘多项式的法则进行计算，再合并同类项即可．
【解答】解：（2x﹣3y）（3x+2y）﹣（2x﹣y）（y+2x）
＝6x2﹣5xy﹣6y2﹣（4x2﹣y2）
＝6x2﹣5xy﹣6y2﹣4x2+y2
＝2x2﹣5xy﹣5y2．
【点评】本题考查了平方差公式和多项式乘多项式，熟练掌握平方差公式和多项式乘多项式的法则是解题的关键．
4．（2024秋•普陀区期中）阅读理解．
已知（a﹣12）2+（14﹣a）2＝6，求（a﹣13）2的值．
解：由（a﹣12）2+（14﹣a）2＝6，可得[（a﹣13）+1]2+[（a﹣13）﹣1]2＝6．
整理得（a﹣13）2+2（a﹣13）+1+（a﹣13）2﹣2（a﹣13）+1＝6．
2（a﹣13）2+2＝6
得（a﹣13）2＝2．
请仿照上述方法，完成下列问题：
（1）已知（a﹣98）2+（96﹣a）2＝10，求（a﹣97）2的值．
（2）已知（a﹣2024）2＝8，求（a﹣2025）2+（2023﹣a）2的值．
【考点】完全平方公式．
【专题】整式；运算能力．
【答案】（1）4；
（2）18．
【分析】（1）将（a﹣98）2+（96﹣a）2＝10变形为[（a﹣97）﹣1]2+[（a﹣97）+1]2＝10，然后利用完全平方公式展开并整理成2（a﹣97）2+2＝10，即可求出（a﹣97）2的值；
（2）将（a﹣2025）2+（2023﹣a）2变形为[（a﹣2024）﹣1]2+[（a﹣2024）+1]2，然后利用完全平方公式展开并整理成2（a﹣2024）2+2，然后将已知条件代入求值即可．
【解答】解：（1）由（a﹣98）2+（96﹣a）2＝10，可得[（a﹣97）﹣1]2+[（a﹣97）+1]2＝10，
整理得（a﹣97）2﹣2（a﹣97）+1+（a﹣97）2+2（a﹣97）+1＝10，
2（a﹣97）2+2＝10，
得（a﹣97）2＝4；
（2）（a﹣2025）2+（2023﹣a）2
＝[（a﹣2024）﹣1]2+[（a﹣2024）+1]2
＝（a﹣2024）2﹣2（a﹣2024）+1+（a﹣2024）2+2（a﹣2024）+1
＝2（a﹣2024）2+2，
当（a﹣2024）2＝8时，
原式＝2×8+2＝18．
【点评】本题考查了完全平方公式，熟练掌握完全平方公式是解题的关键．
5．（2023秋•宜宾期末）如图①是一个长为2a、宽为2b的长方形，沿图中虚线用剪刀均分成四块小长方形，然后按图②的形状拼成一个正方形．
（1）观察图②．请你直接写出下列三个式子：（a+b）2、（a﹣b）2、ab之间的等量关系式为 （a+b）2＝（a﹣b）2+4ab ；
（2）若m、n均为实数，且m+n＝3，mn＝﹣4，且m＜n，运用（1）所得到的公式求m﹣n的值；
（3）如图③，S1、S2分别表示边长为x、y的正方形的面积，且A、B、C三点在一条直线上，若S1+S2＝20，S△BCD+S△ACF＝8，求图中两个正方形的周长之和．
【考点】完全平方公式的几何背景．
【专题】整式；运算能力．
【答案】（1）（a+b）2＝（a﹣b）2+4ab；
（2）m﹣n＝﹣5；
（3）24．
【分析】（1）根据几何意义，得到大正方形的边长为a+b，阴影正方形的边长为a﹣b，每个长方形的长为a，宽为b，根据大正方形的面积等于阴影正方形的面积和4个长方形的面积和，结合面积计算公式解答即可．
（2）根据公式变形，得（m﹣n）2＝（m+n）2﹣4mn，代入计算，结合m＜n，计算即可．
（3）如图③，S1、S2分别表示边长为x、y的正方形的面积，且A、B、C三点在一条直线上，若S1+S2＝20，S△BCD+S△ACF＝8，求图中两个正方形的周长之和．
【解答】解：（1）根据几何意义，得到大正方形的边长为a+b，阴影正方形的边长为a﹣b，每个长方形的长为a，宽为b，根据大正方形的面积等于阴影正方形的面积和4个长方形的面积和，
故（a+b）2＝（a﹣b）2+4ab，
故答案为：（a+b）2＝（a﹣b）2+4ab．
（2）根据（a+b）2＝（a﹣b）2+4ab，变形，得
（m﹣n）2＝（m+n）2﹣4mn，
∵m+n＝3，mn＝﹣4，
∴（m﹣n）2＝32﹣4×（﹣4）＝25，
∴m﹣n＝﹣5，m﹣n＝5，
∵m＜n，
∴m﹣n＝﹣5．
（3）由题可知：S1+S2＝20，
∴x2+y2＝20，
∵S△BCD+S△ACF＝8，
∴12xy+12xy=8，即xy＝8，
∴（x+y）2＝x2+y2+2xy＝36，
∴x+y＝±6，
∵x+y＞0，
∴x+y＝6，
∴4（x+y）＝24，
即两个正方形的周长之和24．
【点评】本题考查了完全平方公式的几何背景，解题的关键是理解题意，灵活运用所学知识解决问题．
二．填空题（共5小题）
6．（2024春•惠山区期中）如果x2+mx+16完全平方式，则m的值等于 8或﹣8 ．
【考点】完全平方式．
【专题】整式；运算能力．
【答案】8或﹣8．
【分析】根据完全平方式得出mx＝±2•x•y，再求出答案即可．
【解答】解：∵x2+mx+16完全平方式，
∴mx＝±2•x•y，
解得：m＝8或﹣8．
故答案为：8或﹣8．
【点评】本题考查了完全平方式，能熟记完全平方式（完全平方式有a2+2ab+b2和a2﹣2ab+b2两个）是解此题的关键．
7．（2024秋•南岗区校级期中）已知：a+b＝3，ab＝5，则a2+b2﹣2a﹣2b+6＝ ﹣1 ．
【考点】完全平方公式．
【专题】整式；运算能力．
【答案】﹣1．
【分析】根据完全平方公式可得a2+b2＝（a+b）2﹣2ab，再把a+b＝3，ab＝5代入计算即可．
【解答】解：∵a+b＝3，ab＝5，
∴a2+b2﹣2a﹣2b+6
＝（a+b）2﹣2ab﹣2（a+b）+6
＝32﹣2×5﹣2×3+6
＝9﹣10﹣6+6
＝﹣1．
故答案为：﹣1．
【点评】本题主要考查了完全平方公式，熟记公式是解答本题的关键．
8．（2024秋•金牛区校级期中）如图，已知边长为a，b的长方形，若它的周长为20，面积为32，则a2+b2的值为 36 ．
【考点】完全平方公式的几何背景．
【专题】整式；运算能力．
【答案】36．
【分析】根据题意得到a+b＝10，ab＝32，再利用完全平方公式变形，整体代入求值即可．
【解答】解：根据题意可知：a+b＝10，ab＝32，
所以原式＝（a+b）2﹣2ab
＝102﹣2×32
＝100﹣64
＝36．
故答案为：36．
【点评】本题考查了完全平方公式的几何背景，掌握完全平方公式的定义是关键．
9．（2024秋•江汉区期中）计算：10012﹣1006×994＝ 2037 ．
【考点】平方差公式．
【专题】整式；运算能力．
【答案】2037．
【分析】先将1006×994写成（1000+6）×（1000﹣6），然后利用平方差公式计算，去括号后再次利用平方差公式计算，最后进行加法运算即可．
【解答】解：10012﹣1006×994
＝10012﹣（1000+6）×（1000﹣6）
＝10012﹣（10002﹣62）
＝10012﹣10002+36
＝（1001+1000）×（1001﹣1000）+36
＝2001+36
＝2037，
故答案为：2037．
【点评】本题考查了平方差公式，熟练掌握平方差公式是解题的关键．
10．（2024秋•黄浦区期中）计算：（2x﹣5y）（2x+5y）＝ 4x2﹣25y2 ．
【考点】平方差公式．
【专题】整式；运算能力．
【答案】4x2﹣25y2．
【分析】根据平方差公式计算即可．
【解答】解：（2x﹣5y）（2x+5y）
＝ （2x）2﹣（5y）2
＝4x2﹣25y2，
故答案为：4x2﹣25y2．
【点评】本题考查了平方差公式，熟练掌握平方差公式是解题的关键．
三．选择题（共5小题）
11．（2024秋•东城区校级期中）若a+b＝3，ab＝﹣12，则a2﹣ab+b2的值为（ ）
A．57B．21C．45D．33
【考点】完全平方公式．
【专题】实数；运算能力．
【答案】C
【分析】先对原式进行变形，再计算即可．
【解答】解：a2﹣ab+b2
＝a2+2ab+b2﹣3ab
＝（a+b）2﹣3ab，
∵a+b＝3，ab＝﹣12，
∴原式＝32﹣3×（﹣12）
＝9+36
＝45．
故选：C．
【点评】本题主要考查完全平方公式，熟练掌握完全平方公式是解题的关键．
12．（2024秋•黄浦区期中）下列各式能用平方差公式计算的是（ ）
A．（a﹣b）（b﹣a）B．（a+b）（b+a）
C．（a﹣b）（﹣a﹣b）D．（a+b）（﹣a﹣b）
【考点】平方差公式；完全平方公式．
【专题】整式；运算能力．
【答案】C
【分析】根据平方差公式、完全平方公式的结构特征逐项判断即可．
【解答】解：A、（a﹣b）（b﹣a）＝﹣（a﹣b）（a﹣b）＝﹣（a﹣b）2＝﹣（a2﹣2ab+b2）＝﹣a2+2ab﹣b2，不能用平方差公式计算，故此选项不符合题意；
B、（a+b）（b+a）＝（a+b）（a+b）＝（a+b）2＝a2+2ab+b2，不能用平方差公式计算，故此选项不符合题意；
C、（a﹣b）（﹣a﹣b）＝﹣（a﹣b）（a+b）＝﹣（a2﹣b2）＝﹣a2+b2，能用平方差公式计算，故此选项符合题意；
D、（a+b）（﹣a﹣b）＝﹣（a+b）（a+b）﹣（a+b）2＝﹣（a2+2ab+b2）＝﹣a2﹣2ab﹣b2，不能用平方差公式计算，故此选项不符合题意；
故选：C．
【点评】本题考查了平方差公式、完全平方公式，熟练掌握这两个公式是解题的关键．
13．（2024秋•金牛区校级期中）若a﹣b＝8，a2+b2＝82，则2ab的值为（ ）
A．9B．﹣9C．18D．﹣18
【考点】完全平方公式．
【专题】整式；运算能力．
【答案】C
【分析】根据完全平方公式进行变形即可求解．
【解答】解：∵a﹣b＝8，a2+b2＝82，
∴（a﹣b）2＝64，
∴a2+b2﹣2ab＝64，
∴82﹣2ab＝64，
∴2ab＝82﹣64＝18．
故选：C．
【点评】本题主要考查完全平方公式，掌握公式的变形是关键．
14．（2023秋•宜宾期末）如图①，在边长为a的正方形中挖掉一个边长为b的小正方形（a＞b），把余下的部分剪拼成一个矩形（如图②），通过计算两个图形的面积，验证了一个等式，则这个等式是（ ）
A．（a+2b）（a﹣b）＝a2+ab﹣2b2
B．a2﹣b2＝（a+b）（a﹣b）
C．（a﹣b）2＝a2﹣2ab+b2
D．（a+b）2＝a2+2ab+b2
【考点】平方差公式的几何背景．
【答案】B
【分析】根据图①中阴影部分的面积和图②的面积，可以列出等式，从而可以解答本题．
【解答】解：由题意可得，
图①中阴影部分的面积是：a2﹣b2，
图②中矩形的面积是：（a+b）（a﹣b），
∴a2﹣b2＝（a+b）（a﹣b），
故选：B．
【点评】本题考查平方差公式的几何背景，解题的关键是明确题意，找出其中的等量关系．
15．（2023秋•楚雄市校级期末）如图，大正方形与小正方形的面积之差是40，则阴影部分的面积是（ ）
A．80B．40C．20D．10
【考点】平方差公式的几何背景．
【专题】整式；运算能力．
【答案】C
【分析】设BC＝a，BD＝b，由拼图可知AE＝a﹣b，a2﹣b2＝40，再利用三角形面积公式分别用代数式表示两个阴影三角形的面积和，再根据平方差公式进行因式分解即可．
【解答】解：设BC＝a，BD＝b，则AE＝a﹣b，a2﹣b2＝40，
所以S阴影部分=12a（a﹣b）+12b（a﹣b）
=12（a+b）（a﹣b）
=12×（a2﹣b2）
=12×40
＝20．
故选：C．
【点评】本题考查平方差公式的几何背景，掌握平方差公式的结构特征是正确解答的关键．
考点卡片
1．多项式乘多项式
（1）多项式与多项式相乘的法则：
多项式与多项式相乘，先用一个多项式的每一项乘另外一个多项式的每一项，再把所得的积相加．
（2）运用法则时应注意以下两点：
①相乘时，按一定的顺序进行，必须做到不重不漏；②多项式与多项式相乘，仍得多项式，在合并同类项之前，积的项数应等于原多项式的项数之积．
2．完全平方公式
（1）完全平方公式：（a±b）2＝a2±2ab+b2．
可巧记为：“首平方，末平方，首末两倍中间放”．
（2）完全平方公式有以下几个特征：①左边是两个数的和的平方；②右边是一个三项式，其中首末两项分别是两项的平方，都为正，中间一项是两项积的2倍；其符号与左边的运算符号相同．
（3）应用完全平方公式时，要注意：①公式中的a，b可是单项式，也可以是多项式；②对形如两数和（或差）的平方的计算，都可以用这个公式；③对于三项的可以把其中的两项看做一项后，也可以用完全平方公式．
3．完全平方公式的几何背景
（1）运用几何直观理解、解决完全平方公式的推导过程，通过几何图形之间的数量关系对完全平方公式做出几何解释．
（2）常见验证完全平方公式的几何图形
（a+b）2＝a2+2ab+b2．（用大正方形的面积等于边长为a和边长为b的两个正方形与两个长宽分别是a，b的长方形的面积和作为相等关系）
4．完全平方式
完全平方式的定义：对于一个具有若干个简单变元的整式A，如果存在另一个实系数整式B，使A＝B2，则称A是完全平方式．
a2±2ab+b2＝（a±b）2
完全平方式分两种，一种是完全平方和公式，就是两个整式的和括号外的平方．另一种是完全平方差公式，就是两个整式的差括号外的平方．算时有一个口诀“首末两项算平方，首末项乘积的2倍中间放，符号随中央．（就是把两项的乘方分别算出来，再算出两项的乘积，再乘以2，然后把这个数放在两数的乘方的中间，这个数以前一个数间的符号随原式中间的符号，完全平方和公式就用+，完全平方差公式就用﹣，后边的符号都用+）”
5．平方差公式
（1）平方差公式：两个数的和与这两个数的差相乘，等于这两个数的平方差．
（a+b）（a﹣b）＝a2﹣b2
（2）应用平方差公式计算时，应注意以下几个问题：
①左边是两个二项式相乘，并且这两个二项式中有一项完全相同，另一项互为相反数；
②右边是相同项的平方减去相反项的平方；
③公式中的a和b可以是具体数，也可以是单项式或多项式；
④对形如两数和与这两数差相乘的算式，都可以运用这个公式计算，且会比用多项式乘以多项式法则简便．
6．平方差公式的几何背景
（1）常见验证平方差公式的几何图形（利用图形的面积和作为相等关系列出等式即可验证平方差公式）．
（2）运用几何直观理解、解决平方差公式的推导过程，通过几何图形之间的数量关系对平方差公式做出几何解释．