安徽省六安市外国语学校2023-2024学年九年级上学期第三次月考数学试题（解析版）-A4

这是一份安徽省六安市外国语学校2023-2024学年九年级上学期第三次月考数学试题（解析版）-A4，共22页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
学校：_______姓名：_______班级：_______考号：_______
一、单选题（40分）
1. 若反比例函数的图象经过点，那么k的值是（ ）
A. 3B. C. D.
【答案】B
【解析】
【分析】根据反比例函数的图象经过点，可以得到，即可得到k的值．
【详解】解：∵反比例函数的图象经过点，
∴，
解得，
故选：B．
【点睛】本题考查反比例函数图象上点的坐标特征，解题的关键是明确反比例函数上点的坐标符合函数关系式．
2. 二次函数的最小值是 （ ）
A. 2B. 2C. 1D. 1
【答案】B
【解析】
【详解】解：对于二次函数的顶点式y=a+k而言，函数的最小值为k.
所以二次函数的最小值为2，
故选：B
3. 若抛物线平移得到，则必须（ ）
A. 先向左平移4个单位，再向下平移1个单位
B. 先向右平移1个单位，再向上平移4个单位
C. 先向左平移1个单位，再向下平移4个单位
D. 先向右平移4个单位，再向上平移1个单位
【答案】D
【解析】
【分析】左右平移改变自变量的值：左加右减；上下平移改变因变量的值：上加下减．
【详解】解：A：平移后抛物线的解析式为：，即，不符合题意；
B：平移后抛物线的解析式为：，即，不符合题意；
C：平移后抛物线的解析式为：，即，不符合题意；
D：平移后抛物线的解析式为：，即，符合题意；
故选：D
【点睛】本题考查二次函数的平移．熟记相关结论即可．
4. 如图，点B在线段AC上，且，设AC＝2，则AB的长为（ ）
A. B. C. D.
【答案】C
【解析】
【分析】根据题意列出一元二次方程，解方程即可．
详解】解：，
，
，
解得，，舍去，
故选C．
【点睛】本题考查的是黄金分割的概念以及黄金比值，掌握一元二次方程的解法是解题的关键．
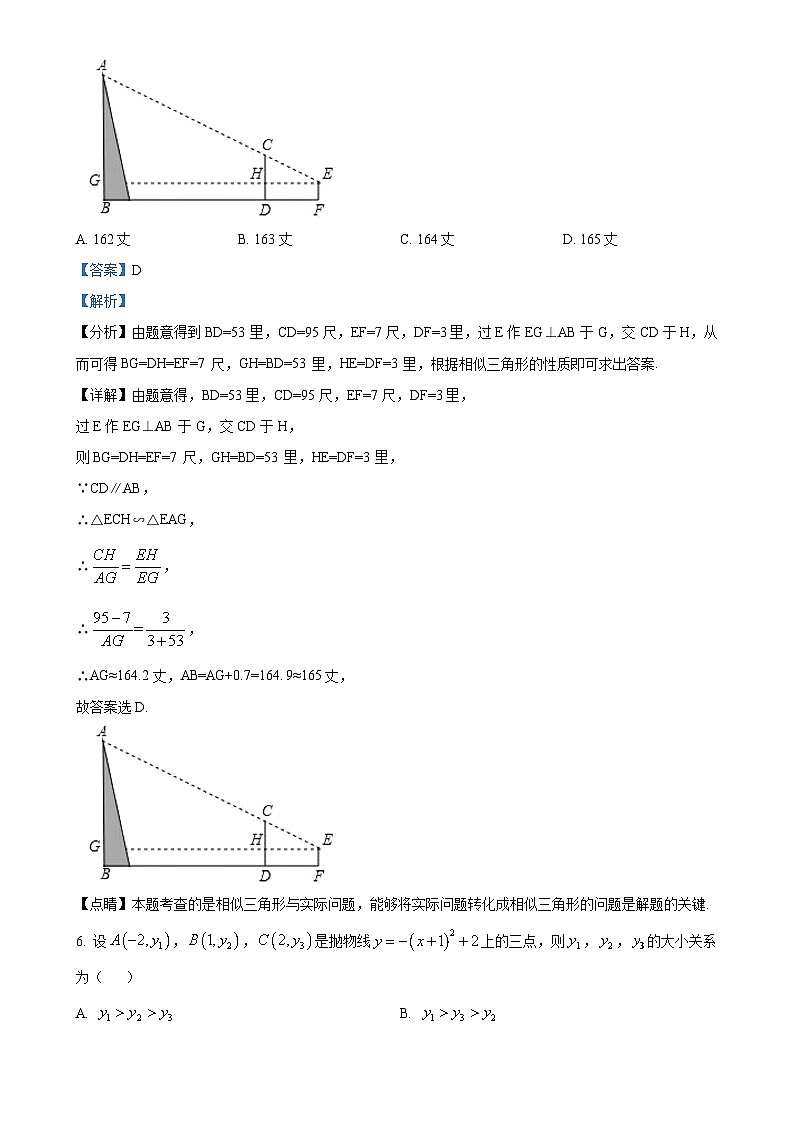
5. 据《九章算术》记载：“今有山居木西，不知其高.山去五十三里，木高九丈五尺.人立木东三里，望木末适与山峰斜平.人目高七尺.问山高几何？”译文如下：如图，今有山位于树的西面.山高为未知数，山与树相距53里，树高9丈5尺.人站在离树3里的地方，观察到树梢恰好与山峰处在同一条直线上，人眼离地7尺.则山高的长为（结果保留到整数，1丈=10尺）( )
A. 162丈B. 163丈C. 164丈D. 165丈
【答案】D
【解析】
【分析】由题意得到BD=53里，CD=95尺，EF=7尺，DF=3里，过E作EG⊥AB于G，交CD于H，从而可得BG=DH=EF=7尺，GH=BD=53里，HE=DF=3里，根据相似三角形的性质即可求出答案.
【详解】由题意得，BD=53里，CD=95尺，EF=7尺，DF=3里，
过E作EG⊥AB于G，交CD于H，
则BG=DH=EF=7尺，GH=BD=53里，HE=DF=3里，
∵CD∥AB，
∴△ECH∽△EAG，
∴，
∴，
∴AG≈164.2丈，AB=AG+0.7=164.9≈165丈，
故答案选D.
【点睛】本题考查的是相似三角形与实际问题，能够将实际问题转化成相似三角形的问题是解题的关键.
6. 设，，是抛物线上的三点，则，，的大小关系为（ ）
A. B.
C. D.
【答案】A
【解析】
【分析】把点的坐标分别代入抛物线解析式可求得y1，y2，y3的值，比较大小即可．
【详解】解：∵，，是抛物线上的三点，
∴，，，
∵1＞-2＞-7，
∴，
故选：A．
【点睛】本题主要考查二次函数图象上点的坐标特征，掌握函数图象上点的坐标满足函数解析式是解题的关键．
7. 如图，△ABC与△DEF都是正方形网格中的格点三角形（顶点在格点上），那么△ABC与△DEF的周长比为（ ）
A. B. 1：2C. 1：3D. 1：4
【答案】A
【解析】
【分析】设正方形网格的边长为1，根据勾股定理求出△EFD、△ABC的边长，运用三边对应成比例，则两个三角形相似这一判定定理证明△BAC∽△EDF，即可解决问题．
【详解】解：如图，设正方形网格的边长为1，
由勾股定理得：
DE2＝22+22，EF2＝22+42，
∴DE＝2，EF＝2；
同理可求：AC＝，BC＝，
∵DF＝2，AB＝2，
∴，
∴△BAC∽△EDF，
∴C△ABC：C△DEF＝1：，
故选A．
【点睛】本题主要考查了勾股定理和相似三角形的判定及其性质定理的应用问题，熟练掌握相似三角形的判定与性质是解题的关键．
8. 如图，在Rt△ABC中，BAC=°，以其三边为边分别向外作正方形，延长EC，DB分别交GF，AH于点N，K，连结KN交AG于点M，若S1-S2=2，AC=4，则AB的长为 （ ）
A. 2B. C. D.
【答案】A
【解析】
【分析】先证≌，根据全等三角形的性质可得AB=FN；再证△BCK∽△ACB，根据相似三角形的性质可得；设五边形ACFNM的面积为S，可得S1+S2=S正方形ACFG=AC2=16， S2+S= S梯形CFNK==，设AB=x，BC=y，可得方程组 ，解方程组即可求解．
【详解】∵∠ACB+∠CAN=90°，∠FCN+∠CAN=90°，
∴∠ACB=∠FCN，
在△ABC和△FCN中，
，
∴≌，
∴AB=FN；
∵∠BAC=∠KBC=90°，
∴△BCK∽△ACB，
∴，
∴；
设五边形ACFNM的面积为S，
∵S1-S2=2，
∴（S1+S）-（S2+S）=2，
设AB=x，BC=y，
由勾股定理可得，，
∵S1+S2=S正方形ACFG=AC2=16， S2+S= S梯形CFNK=，S1-S2=2，
∴（S1+S）-（S2+S）=16-=16-=2，
∴ ，
解得，，，，，
∵x、y都为正数，
∴，
即AB=2，BC=．
故选A．
【点睛】本题考查了正方形的性质、勾股定理、全等三角形的判定与性质及相似三角形的判定与性质，熟练运用相关知识是解决问题的关键．
9. 如图，点A，B，C在⊙O上，∠AOB=72°，则∠ACB等于（ ）

A. 36°B. 54°C. 18°D. 28°
【答案】A
【解析】
【分析】由圆周角定理即可求出.
【详解】根据圆周角定理可知，∠AOB=2∠ACB=72°，则∠ACB=36°，故选A．
【点睛】此题主要考查圆周角定理，解题的关键是熟知圆周角定理的应用.
10. 已知，等边三角形和正方形的边长相等，按如图所示的位置摆放（C点与E点重合），点共线，沿方向匀速运动，直到B点与F点重合．设运动时间为，运动过程中两图形重叠部分的面积为，则下面能大致反映与之间关系的函数图象是（ ）

A. B.
C. D.
【答案】A
【解析】
【分析】分点C在EF中点的左侧、点C在EF中点的右侧、点C在F点右侧且B在EF中点的左侧，点C在F点右侧且B在EF中点的右侧四种情况，分别求出函数的表达式即可求解．
【详解】解：设等边三角形ABC和正方形DEFG的边长都为a，运动速度为1，
当点C在EF的中点左侧时，

设AC交DE于点H，
则CE=t，HE=ECtan∠ACB=t×=t，
则S=S△CEH=×CE×HE=×t×t=，
可知图象为开口向上的二次函数，
当点C在EF的中点右侧时，设AB与DE 交于点M，

则EC=t，BE=a-t，ME=，
∴S=，
可知图象为开口向下的二次函数；
当点C在F点右侧且B在EF中点的左侧时，

S=，
可知图象为开口向下的二次函数；
当点C在F点右侧且B在EF中点的右侧时，

此时BF=2a-t，MF=，
∴，
可知图象为开口向上的二次函数；
故选：A
【点睛】本题考查的是动点图象问题，此类问题关键是：弄清楚不同时间段，图象和图形的对应关系，进而求解．
二、填空题（20分）
11. 抛物线与x轴交于两点，分别是，，则________
【答案】2
【解析】
【分析】与轴交点即令中，再由根与系数的关系得到即可．
【详解】解：由题意得令，
∴，其两根为，
∴，
故答案为：．
【点睛】本题考查二次函数与一元二次方程的关系，与轴的交点即令二次函数中得到对应的一元二次方程．
12. 如图，三个顶点分别在边长为的正方形网格的格点上，则________．（填“”“”“”）
【答案】
【解析】
【分析】根据正切的概念和正方形网格图求出tanα和tanβ，根据等腰直角三角形的性质和tan45°的值求出tan（α＋β），比较即可．
【详解】由正方形网格图可知，tanα＝，tanβ＝，
则tanα＋tanβ＝＋＝，
∵AC＝BC，∠ACB＝90°，
∴α＋β＝45°，
∴tan（α＋β）＝1，
∴tan（α＋β）＞tanα＋tanβ，
故答案为：＞
【点睛】本题考查的是特殊角的三角函数值、锐角三角函数的定义以及等腰直角三角形的性质，熟记特殊角的三角函数值、正确理解锐角三角函数的定义是解题的关键．
13. 如图，点A在二次函数y＝ax2(a＞0)第一象限的图象上，AB⊥x轴，AC⊥y轴，垂足分别为B、C，连接BC，交函数图象于点D，DE⊥y轴于点E，则的值为______.
【答案】
【解析】
【分析】设A(m，am2)，则B(m，0)，C(0，am2)，根据待定系数法求得直线BC的解析式，然后联立方程求得D的横坐标即可求得的值.
【详解】设A(m，am2)，则B(m，0)，C(0，am2)，
设直线y＝kx+b，
∴，解得，
∴y＝﹣amx+am2，
解得x1＝m，x2＝m(舍去)，
∵DE⊥y轴于点E，
∴DE＝m，
∴＝＝.
故答案为.
【点睛】本题主要考查了二次函数的综合运用，熟练掌握相关概念是解题关键.
14. 如图，正方形ABCD的边长是6，对角线的交点为O，点E在边CD上且，，连接OF，则（1）_______；（2）________；
【答案】 ①. 45° ②.
【解析】
【分析】如图，在BE上截取线段BG，使得BG=CF，可求得，根据勾股定理求解相应线段的长度即可．
【详解】解：如图，在BE上截取线段BG，使得BG=CF，
在正方形ABCD中，AB=BC=CD=DA=6，，
，，
∵，
∴，
∴，
∴，
∴（SAS），
∴，，
∴，
∴为等腰直角三角形，，
在中，由勾股定理可得：，
则，
在中，由勾股定理可得：
∴，
在中，由勾股定理可得：，即
解得，
故答案为：45°，
【点睛】此题考查了正方形的性质，全等三角形的判定与性质，勾股定理以及等腰三角形的判定与性质，解题的关键是作出合适的辅助线，找到全等三角形．
三、解答题（90分）
15. 计算：
【答案】
【解析】
【分析】将特殊角的三角函数值代入求解．
【详解】解：原式，
．
【点睛】本题考查了特殊角的三角函数值，解答本题的关键是掌握几个特殊角的三角函数值，属于基础题．
16. 如图，的三个顶点坐标分别是．
（1）以原点O为位似中心，在y轴左侧画出，使得与的位似比为2∶1；
（2）的内部一点M的坐标为，则点M在中的对应点的坐标是多少？
【答案】（1）见解析 （2）
【解析】
【分析】(1)依据位似中心及位似比的大小即可作出；
(2)根据位似比和位似图形的位置即可求解．
【小问1详解】
解：如图所示，
【小问2详解】
∵与位似比为2∶1，在y轴左侧，
∴内部一点M的坐标为，则点M在中的对应点的坐标是
【点睛】本题考查了位似变换，能根据位似中心找到位似图形中对应点的位置是解题的关键．
17. 如图，已知一次函数y=kx+b的图象与x轴交于点A，与反比例函数 （x＜0）的图象交于点B（﹣2，n），过点B作BC⊥x轴于点C，点D（3﹣3n，1）是该反比例函数图象上一点．
（1）求m的值；
（2）若∠DBC=∠ABC，求一次函数y=kx+b的表达式．
【答案】（1）-6；（2）．
【解析】
【分析】（1）由点B（﹣2，n）、D（3﹣3n，1）在反比例函数（x＜0）的图象上可得﹣2n=3﹣3n，即可得出答案；
（2）由（1）得出B、D的坐标，作DE⊥BC．延长DE交AB于点F，证△DBE≌△FBE得DE=FE=4，即可知点F（2，1），再利用待定系数法求解可得．
【详解】解：（1）∵点B（﹣2，n）、D（3﹣3n，1）在反比例函数（x＜0）的图象上，
∴，解得：；
（2）由（1）知反比例函数解析式为，∵n=3，∴点B（﹣2，3）、D（﹣6，1），
如图，过点D作DE⊥BC于点E，延长DE交AB于点F，
在△DBE和△FBE中，∵∠DBE=∠FBE，BE=BE，∠BED=∠BEF=90°，
∴△DBE≌△FBE（ASA），∴DE=FE=4，
∴点F（2，1），将点B（﹣2，3）、F（2，1）代入y=kx+b，
∴，解得：，
∴．
【点睛】本题主要考查了反比例函数与一次函数的综合问题，解题的关键是能借助全等三角形确定一些相关线段的长．
18. 张老师家的洗手盆上装有一种抬启式水龙头（如图①），完全开启后，把手与水平线的夹角为，此时把手端点、出水口点和落水点在同一直线上．洗手盆及水龙头示意图如图②，其相关数据为，，，．求的长（结果精确到．参考数据：，，，）．
【答案】27.7cm
【解析】
【分析】本题考查了相似三角形的应用以及三角函数的应用，在运用数学知识解决问题过程中，关注核心内容，经历测量、运算、建模等数学实践活动为主线的问题探究过程，突出考查数学的应用意识和解决问题的能力，蕴含数学建模，引导学生关注生活，利用数学方法解决实际问题．
作于G，则，由三角函数求出，，，，得出．
【详解】如图，作
则，
，
，
∴


∴
∴
答：的长是27.7cm．
19. 如图，在中，，以为直径作交于点，过点作，垂足为，且交的延长线与点．
（1）求证：是的切线；
（2）若，，求的长．
【答案】（1）见解析；（2）4
【解析】
【分析】（1）作辅助线，根据等腰三角形三线合一得BD=CD，根据三角形的中位线可得OD∥AC，所以得OD⊥EF，从而得结论；
（2）根据等腰三角形三线合一的性质证得∠BAD=∠BAC=30°，由30°的直角三角形的性质即可求得BD．
【详解】解：（1）证明：连接OD，AD，
∵AB是⊙O直径，
∴AD⊥BC，
∵AB=AC，
∴BD=CD，
∵OA=OB，
∴OD∥AC，
∵EF⊥AC，
∴OD⊥EF，
∴EF是⊙O的切线；
（2）∵AB=AC，AD⊥BC，
∴∠BAD=∠BAC=30°，
∴BD=AB=×8=4．
【点睛】本题主要考查的是圆的综合应用，解答本题主要应用了圆周角定理、等腰三角形的性质，圆的切线的判定，30°的直角三角形的性质，掌握本题的辅助线的作法是解题的关键．
20. 如图，上午9时，一条船从A处出发，以每小时40海里的速度向正东方向航行，9时30分到达B处，从A，B两处分别测得小岛C在北偏东45°和北偏东15°．
（1）求∠C的度数；
（2）求B处船与小岛C的距离（结果保留根号）．
【答案】（1）30° （2）
【解析】
【分析】（1）根据三角形的内角和定理即可得到结论；
（2）过点B作BD⊥AC与点D，根据已知可求得BD的长，再根据三角函数即可求得BC的长．
【小问1详解】
解：由题意可知∠ABC＝90°＋15°＝105°，
∴∠C＝180°－105°－45°＝30°．
【小问2详解】
解：作BD⊥AC于D点，则∠ADB=∠BDC=90°，
在Rt△ABD中，，∠BAC＝45°，
∴，
在Rt△CBD中，∠C＝30°，
∴．
即B处船与小岛C的距离为海里．
【点睛】本题考查解直角三角形的应用﹣方向角问题，解题的关键是把一般三角形的问题可以转化为解直角三角形的问题，解决的方法就是作高线．
21. 如图，在四边形ABCD中，AB∥CD，∠A=90°，AB=2，AD=5，P是AD上一动点（点P不与A、D重合），PE⊥BP，PE交DC于点E．
（1）求证：△ABP∽△DPE；
（2）设AP=x，DE=y，求y与x之间的函数关系式，并写出x的取值范围；
（3）请你探索在点P运动的过程中，四边形ABED能否构成矩形？如果能，求出AP的长；如果不能，请说明理由．
【答案】（1）见解析；（2）（x≠5）；（3）能，当或时，四边形能构成矩形．
【解析】
【分析】（1）根据同角的余角相等得到，根据相似三角形的判定定理证明结论；
（2）根据相似三角形的性质列出比例式，计算即可；
（3）根据矩形的判定定理、结合一元二次方程计算即可．
【详解】（1）证明：，
，
，
，
，
，，
，
；
（2），
，即，
则，；
（3）当四边形为矩形时，，即，
则，
解得，，，
当或时，四边形能构成矩形．
【点睛】本题考查的是相似三角形的判定和性质、矩形的判定和性质，掌握相关的性质定理和判断定理是解题的关键，注意函数思想在解题中的灵活运用．
22. 已知菱形ABCD中，AB=8，点G是对角线BD上一点，CG交BA的延长线于点F．
（1）求证：CG2=GE•GF；
（2）如果DG=GB，且AG⊥BF，求cs∠F．

【答案】（1）证明见解析；（2）；
【解析】
【分析】（1）利用菱形的性质易证△ADG≌△CDG，由全等三角形的性质可得：∠DAG=∠DCG，再根据菱形的性质可得∠F=∠DCG=∠DAG，所以△GAE∽△GFA，由相似三角形的性质即可证明CG2=GE•GF；
（2）易证△DAG∽△DBA，由相似三角形的性质可得AD2=DG•BD，再利用已知条件可证明∠ABD=∠DAG=∠F，进而可得到csF=cs∠ABG的值．
【详解】∵四边形ABCD是菱形，
∴CD=AD，∠CDG=∠ADG，

在△ADG和△CDG中，，
∴△ADG≌△CDG（SAS），
∴∠DAG=∠DCG，CG=AG
∵BF∥CD，
∴∠F=∠DCG=∠DAG，
∴△GAE∽△GFA，
∴AG2=GE•GF，
∴CG2=GE•GF；
（2）∵BF∥CD，DG=GB，
∴，
∴BF=2CD=16，AF=8，
∴∠ABD=∠DAG=∠F，
∴△DAG∽△DBA，
∴AD2=DG•BD，
∴DG=，BG=，
∴csF=cs∠ABG=．
【点睛】本题考查的知识点是菱形的性质及相似三角形的判定与性质，解题的关键是熟练的掌握菱形的性质及相似三角形的判定与性质.
23. 如图，在平面直角坐标系中，反比例函数y＝（x＞0）的图象经过点A（2，6），将点A向右平移2个单位，再向下平移a个单位得到点B，点B恰好落在反比例函数y＝（x＞0）的图象上，过A，B两点的直线y＝k2x+b与y轴交于点C．
（1）求a的值及点C的坐标．
（2）在y轴上有一点D（0，5），连接AD，BD，求△ABD的面积．
（3）结合图象，直接写出≤k2x+b的解集．
【答案】（1）；C（0，9）；（2）S△ABD＝；（3）
【解析】
【分析】（1）由点A（2，6）求出反比例函数的解析式为y＝，进而求得B（4，3），由待定系数法求出直线AB的解析式为y＝−x＋9，即可求出C点的坐标；
（2）由（1）求出CD，根据S△ABD＝S△BCD−S△ACD可求得结论；
（3）直接根据函数图像解答即可．
【详解】解：（1）把点A（2，6）代入y＝，＝2×6＝12，
∴反比例函数的解析式为y＝，
∵将点A向右平移2个单位，
∴x＝4，
当x＝4时，y＝＝3，
∴B（4，3），
∴，
直线AB的解析式为y＝k2x+b，
由题意可得，
解得，
∴y＝−x＋9，
当x＝0时，y＝9，
∴C（0，9）；
（2）由（1）知CD＝9−5＝4，
∴S△ABD＝S△BCD−S△ACD＝CD•|xB|−CD•|xA|＝×4×4−×4×2＝4；
（3）∵A（2，6）,B（4，3），
根据图像可知≤k2x+b的解集为．
【点睛】本题考查了反比例函数系数k的几何意义，待定系数法求函数的解析式，三角形的面积的计算，求得直线AB的解析式是解题的关键．