高中物理人教版 (2019)选择性必修 第三册第二章 气体、固体和液体3 气体的等压变化和等容变化精品课件ppt

这是一份高中物理人教版 (2019)选择性必修 第三册第二章 气体、固体和液体3 气体的等压变化和等容变化精品课件ppt，共59页。PPT课件主要包含了新课导入，气体的等压变化，PART01，等压变化，实验视频，等压图像，盖吕萨克定律，盖吕萨克生平介绍，等压线，微观解释等内容，欢迎下载使用。
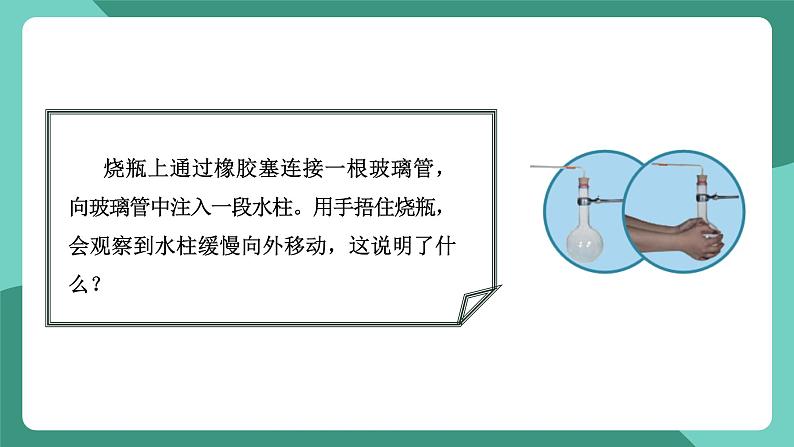
烧瓶上通过橡胶塞连接一根玻璃管，向玻璃管中注入一段水柱。用手捂住烧瓶，会观察到水柱缓慢向外移动，这说明了什么？
1．等压变化：一定质量的某种气体，在压强不变时，体积随温度的变化叫做等压变化．
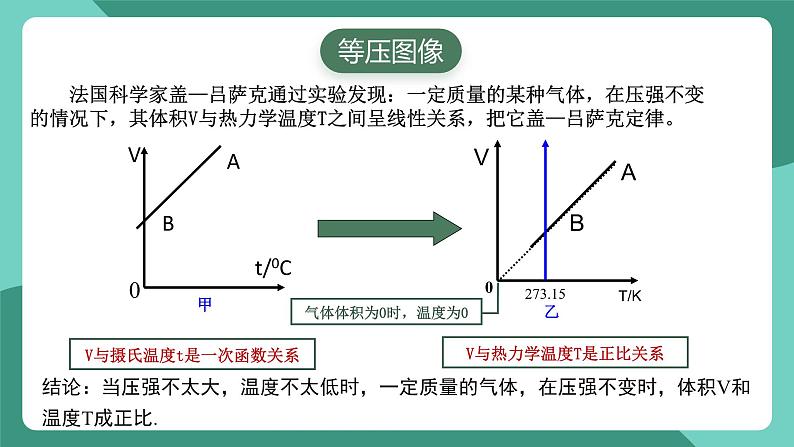
法国科学家盖—吕萨克通过实验发现：一定质量的某种气体，在压强不变的情况下，其体积V与热力学温度T之间呈线性关系，把它盖—吕萨克定律。
结论：当压强不太大，温度不太低时，一定质量的气体，在压强不变时，体积V和温度T成正比.
气体体积为0时，温度为0
V与摄氏温度t是一次函数关系
V与热力学温度T是正比关系
2.盖—吕萨克定律内容：一定质量的某种气体，在压强不变的情况下，其体积V与热力学温度T成正比。 即T T
式中V1、T1表示气体在1（初态）、V2、T2表示2（末态）
这里的C和玻意耳定律查理定律表达式中的C都泛指比例常数，它们并不相等。
4. 适用范围：①温度不太低（与室温相比），压强不太大（与大气压相比） ②气体的质量和体积都不变。
注意：V与热力学温度T成正比，不与摄氏温度t成正比，但体积的变化V与摄氏温度t的变化成正比。V  t(T)
盖·吕萨克（UsephLllis Gay—lussac，1778—1850年）法国化学家、物理学家.
盖·吕萨克1778年9月6日生于圣·莱昂特。1800年毕业于巴黎理工学校. 1850年5月9日，病逝于巴黎，享年72岁.
1802年，盖·吕萨克发现气体热膨胀定律(即盖·吕萨克定律)压强不变时，一定质量气体的体积跟热力学温度成正比.即V1/T1=V2/T2=……=C恒量.
其实查理早就发现体积与温度的关系，只是当时未发表，也未被人注意。直到盖-吕萨克重新提出后，才受到重视。早年都称“查理定律”，但为表彰盖-吕萨克的贡献而称为“查理-盖吕萨克定律”.
（1）等压线：一定质量的某种气体在等压变化过程中，体积随温度变化关系的直线，叫做等压线。
(2)等压线的特点：一定质量的气体的V—T图线其延长线过坐标原点（过原点的倾斜直线）。
答：热力学绝对零度不可能达到。
想一想：为什么Ｏ点附近用虚线？
④V－t图象：在等压变化过程中，体积V与摄氏温度t是一次函数关系，不是简单的正比例关系，如图乙所示，等压线是一条延长线通过横轴上－273.15 ℃的倾斜直线，且斜率越大，压强越小.图象纵轴的截距V0是气体在0 ℃时的体积.
①一定质量的气体的V—T图线其延长线过坐标原点（过原点的倾斜直线），斜率反映压强大小。
②图线上每一个点表示气体一个确定的状态，同一根等压线上各状态的压强相同。
③不同压强下的等压线，斜率越大，压强越小（同一温度下，体积大的压强小）。
（3）V－T和V－t图像：
⑤盖—吕萨克定律的微观解释:
一定质量（m）的理想气体的总分子数（N)是一定的，要保持压强（p）不变，当温度（T）升高时，全体分子运动的平均速率V会增加，那么单位体积内的分子数（n）一定要减小（否则压强不可能不变），因此气体体积一定增大；反之当温度降低时，同理可推出气体体积一定减小。
注意：条件中的“温度不太低（与室温相比），压强不太大（与大气压相比）”的含义： 相当于大气压几倍的压强都可以算作“压强不太大”，零下几十摄氏度的温度也可以算作“温度不太低”。
【例题1】一容器中装有某种气体，且容器上有一个小口与外界大气相通，原来容器内的温度为27℃，若把它加热到127℃，从容器中溢出的空气质量是原来质量的多少倍呢？
初态  T1=300K V1=V P1=P
分析：容器上有一个小口与外界大气相通，即气体的压强始终等于外界大气压，气体状态变化可以看作是等压变化。本题解题的关键不是气体状态的确定，而是研究对象的选取。
末态  T2=400K V2=？ P2=P
就容器而言，里面气体质量变了，但可视容器中气体出而不走，以原来容器中的气体为研究对象，就可以运用气体的等压变化规律求解。气体状态变化如图所示。
以后来容器中的气体为研究对象。气体状态变化如图所示。
初态  T1=400K V1=V P1=P
末态  T2=300K V2=？ P2=P
1、如图所示，两个水平固定的汽缸由管道连通．活塞a、b用刚性杆相连，可在汽缸内无摩擦地移动，缸内及管中封有一定质量的理想气体．整个系统处于平衡状态，大气压强不变．现令缸内气体的温度缓慢升高一点，则系统再次达到平衡状态时(　　)A．活塞向左移动一点，缸内气体压强不变B．活塞向左移动一点，缸内气体压强增大C．活塞向右移动一点，缸内气体压强不变D．活塞的位置没有改变，缸内气体压强增大
解析：因左、右汽缸中的气体的压强相等，若缸内气体的温度缓慢升高一点时，则气体体积变大，因右侧汽缸横截面积较大，则活塞向左移动一点，故选A.
2. 如图甲所示，质量M＝10 kg的导热汽缸置于水平地面上，用质量和厚度均不计的水平导热活塞密封一定质量的理想气体，气体温度为300 K．一质量m＝1 kg的重物用轻绳经光滑滑轮与汽缸中活塞竖直相连接，重物和活塞均处于静止状态，这时活塞离缸底的高度L0＝10 cm，不计活塞与汽缸间的摩擦，且汽缸不漏气．已知大气压强p0＝1×105 Pa，活塞的横截面积为S＝10－2 m2，g取10 m/s2，下列两种情况中，活塞均未脱离汽缸．(1)若将图甲中环境温度缓慢降低至240 K，求此时活塞离汽缸底的高度；(2)若保持图甲中环境温度为300 K不变，将汽缸从图甲状态变为图乙状态，用轻绳将汽缸和活塞竖直悬挂在天花板上，稳定后处于静止状态，求稳定后活塞离汽缸底的高度．
为什么夏天汽车轮胎打气太足，容易爆胎。
利用高压锅可以很快把饭煮熟。
轮胎和高压锅都是气体体积不变，温度升高，压强增大。
相传三国时期著名的军事家、政治家诸葛亮被司马懿困于平阳,无法派兵出城求救。就在此关键时刻,诸葛亮发明了一种可以升空的信号灯——孔明灯,并成功进行了信号联络,其后终于顺利脱险。你知道孔明灯为什么能够升空吗?
简答:孔明灯是利用火焰的热量使容器内的气体膨胀,使部分气体从孔明灯内溢出,进而使孔明灯内气体的质量减少,当大气对孔明灯的浮力恰好等于孔明灯的重力时,即达到孔明灯升空的临界条件,若继续升温,孔明灯就能升空了。
1．等容变化：一定质量的某种气体，在体积不变时，压强随温度的变化叫做等容变化．
法国科学家查理在分析了实验事实后发现：当气体的体积一定时，各种气体的压强与温度之间都有线性关系，把它叫做查理定律。
结论：当压强不太大，温度不太低时，一定质量的气体，在体积不变时，压强p和温度T成正比.
气体压强为0时，温度为0
P与摄氏温度t是一次函数关系
P与热力学温度T是正比关系
2.查理定律内容：一定质量的某种气体，在体积不变的情况下，压强P与热力学温度T成正比。 即p T
式中p1、T1表示气体在1（初态）、p2、T2表示2（末态）
这里的C和玻意耳定律表达式中的C都泛指比例常数，它们并不相等。
4. 适用范围：①温度不太低，压强不太大 ②气体的质量和体积都不变。
一定质量的气体，在体积不变的条件下，压强的变化量与热力学温度的变化量（等于摄氏温度变化量t ）成正比。
注意：p与热力学温度T成正比，不与摄氏温度t成正比，但压强的变化P与摄氏温度t的变化成正比。P  t(T)
（1）等容线：一定质量的某种气体在等容变化过程中，压强随温度变化关系的直线，叫做等容线。
(2)等容线的特点：一定质量的气体的p—T图线其延长线过坐标原点（过原点的倾斜直线）。
P-t图象变化为P-T图象
把交点作为坐标原点，建立新的坐标系，那么，这时的压强与温度的关系就是正比例关系了。
在等容变化过程中，p-t是一次函数关系，不是简单的正比例关系。
如果把直线AB延长至与横轴相交，交点坐标是－273.150C
（3）p－T和p－t图像：
④p－t图象：在等容变化过程中，压强p与摄氏温度t是一次函数关系，不是简单的正比例关系，如图乙所示，等容线是一条延长线通过横轴上－273.15 ℃的倾斜直线，且斜率越大，体积越小.图象纵轴的截距p0是气体在0 ℃时的压强.
①一定质量的气体的P—T图线其延长线过坐标原点（过原点的倾斜直线），斜率反映体积大小。
②图线上每一个点表示气体一个确定的状态，同一根等容线上各状态的体积相同。
③不同体积下的等容线，斜率越大，体积越小（同一温度下，压强大的体积小）。
一定质量（m）的气体的总分子数（N）是一定的，体积（V）保持不变时，其单位体积内的分子数（n）也保持不变，当温度（T）升高时，其分子运动的平均速率（v）也增大，则气体压强（p）也增大；反之当温度（T）降低时，气体压强（p）也减小。
⑤查理定律的微观解释:
我国民间常用“拔火罐”来治疗某些疾病，即用一个小罐，将纸燃烧后放入罐内，然后迅速将火罐开口端紧压在人体的皮肤上，待火罐冷却后，火罐就被紧紧地“吸”在皮肤上。你知道其中的道理吗？答案：火罐内的气体体积一定，冷却后气体的温度降低，压强减小，故在大气压力作用下被“吸”在皮肤上。
【例题】某种气体在状态A时压强2×105Pa，体积为1m3，温度为200K，(1)它在等温过程中由状态A变为状态B，状态B的体积为2m3，求状态B的压强。(2)随后，又由状态B在等容过程中变为状态C，状态C的温度为300K，求状态C的压强。
等温变化，根据 pAVA=pBVB
2×105×1=PB×2
PC=1.5×105Pa
总结：利用查理定律解题的一般步骤(1)确定研究对象，即被封闭的气体。(2)分析被研究气体在状态变化时是否符合定律成立的条件，即是否是质量和体积保持不变。(3)确定初、末两个状态的温度、压强。(4)按查理定律公式列式求解，并对结果进行讨论。
1．(湖北武汉2022高二下期中)民间常用“拔火罐”来治疗某些疾病，方法是将点燃的纸片放入一个小罐内，当纸片燃烧完时，迅速将火罐开口端紧压在皮肤上，火罐就会被紧紧地“吸”在皮肤上．其原因是当火罐内的气体( )A．温度不变时，体积减小，压强增大B．体积不变时，温度降低，压强减小C．压强不变时，温度降低，体积减小D．质量不变时，压强增大，体积减小
解析：把火罐扣在皮肤上，罐内空气的体积等于火罐的容积，之后罐内气体温度不断降低，气体发生等容变化，由查理定律可知，气体压强减小，火罐内气体压强小于外界大气压强，压强差就将火罐紧紧地压在皮肤上．故选B.
2、如图所示，A、B两容器容积相等，用粗细均匀的细玻璃管连接，两容器内装有不同气体，细管中央有一段水银柱，在两边气体作用下保持平衡时，A中气体的温度为273 K，B中气体的温度为293 K，如果将它们的温度都降低10 K，则水银柱将(　　)A．向A移动 B．向B移动C．不动 D．不能确定
查理定律与盖·吕萨克定律的比较
压强不太大(相对大气压)，温度不太低(相对室温)
(1)现实生活中，自行车轮胎在烈日下暴晒，车胎内气体的变化是等容过程。 (　　)(2)一定质量的气体，等容变化时，气体的压强和温度不一定成正比。 (　　)(3)气体的温度升高，气体的体积一定增大。 (　　)
『选一选』(多选)(2020·安徽省淮北市第一中学高二下学期期中)在下列图中，可能反映理想气体经历了等压变化→等温变化→等容变化后，又回到原来状态的有(　　)解析：由图可看出经历了“等压变化”→“等温变化”→“等容变化”后，又回到原来状态的是A、C。
1.（多选）下列关于盖·吕萨克定律的说法中正确的是( ) A、对于一定质量的气体,在保持压强不变的情况下,温度每升高1℃时,其体积的增量是原来体积的1/273 B、对于一定质量的气体.在保持压强不变的情况下,温度每升高1℃时,其体积的增量是它在0℃时体积的1/273 C、对于一定质量的气体,在保持压强不变的情况下,其体积与温度成正比 D、对于一定质量的气体,在保持压强不变的情况下,其体积与热力学温度成正比
3．如图所示，某同学用封有气体的玻璃管来测绝对零度，当容器中水温是30 ℃时，空气柱的长度为30 cm，当水温是90 ℃时，空气柱的长度是36 cm，则该同学测得的绝对零度相当于(　　)A．－273 ℃ B．－270 ℃C．－268 ℃ D．－271 ℃
4、如图所示，在一端开口的钢制圆筒的开口端上面放一活塞，活塞与筒壁间的摩擦及活塞的重力不计，现将其开口端向下，竖直缓慢地放入280 K的水中，在筒底与水面相平时，恰好静止在水中，这时筒内气柱长为14 cm，当水温升高到300 K时，筒底露出水面的高度为多少？(筒的厚度不计，取T＝t＋273 K)
5、如图所示，封闭有一定质量理想气体的汽缸开口向下竖直固定放置，活塞的截面积为S，质量为m0，活塞通过轻绳连接了一个质量为m的重物。若开始时汽缸内理想气体的温度为T0，轻绳刚好伸直且对活塞无拉力作用，外界大气压强为p0，一切摩擦均不计且m0gΔp2，水银柱所受合外力方向向上，应向上移动，若Δp1Δp2，即水银柱上移。
7．如图所示，封闭有一定质量理想气体的汽缸开口向下竖直固定放置，活塞的截面积为S，质量为m0，活塞通过轻绳连接了一个质量为m的重物。若开始时汽缸内理想气体的温度为T0，轻绳刚好伸直且对活塞无拉力作用，外界大气压强为p0，一切摩擦均不计且m0g