
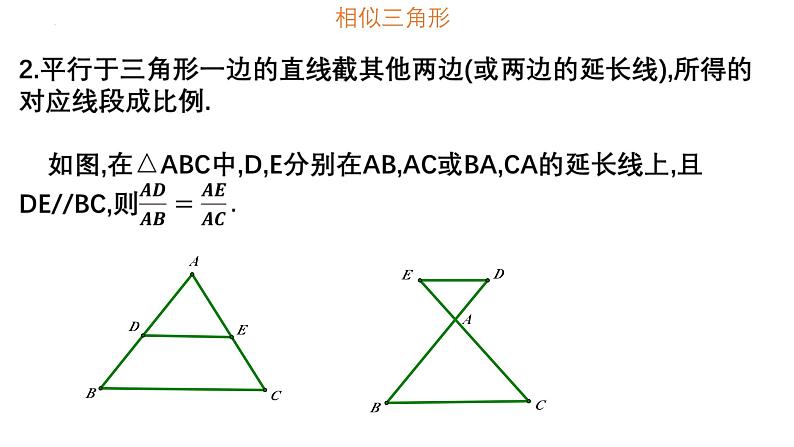


所属成套资源:2025年中考数学一轮教材复习课件(通用版)
2024年九年级数学中考一轮复习之相似三角形模型梳理课件
展开
这是一份2024年九年级数学中考一轮复习之相似三角形模型梳理课件,共60页。PPT课件主要包含了相似三角形,②反“A”字模型,①“8”字模型,对角互补相似,对角互补相似3,相似三角形之半角模型,相交弦定理,切割线定理,∵BE是⊙O的直径,又∵∠A∠A等内容,欢迎下载使用。
知识点二:相似三角形的判定.
1.平行于三角形一边的直线和其他两边相交所构成的三角形与 原三角形相似.2. 三边成比例的两个三角形相似.3.两边成比例且夹角相等的两个三角形相似.4.两角分别相等的两个三角形相似.
知识点三:相似三角形的性质.
1.相似三角形的对应角相等.2.相似三角形的对应边成比例.3.相似三角形的对应高的比、对应角平分线的比、对应中线的比都等于相似比.4.相似三角形的周长比等于相似比.5.相似三角形的面积比等于相似比的平方.
相似三角形复习模型整理
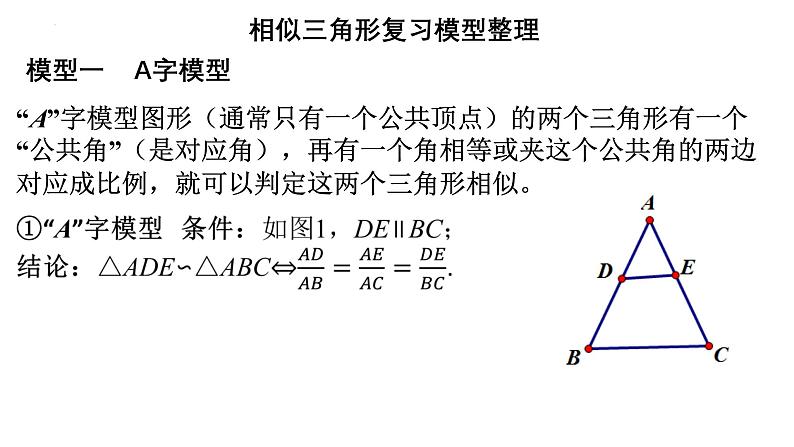
模型一 A字模型
“A”字模型图形(通常只有一个公共顶点)的两个三角形有一个“公共角”(是对应角),再有一个角相等或夹这个公共角的两边对应成比例,就可以判定这两个三角形相似。
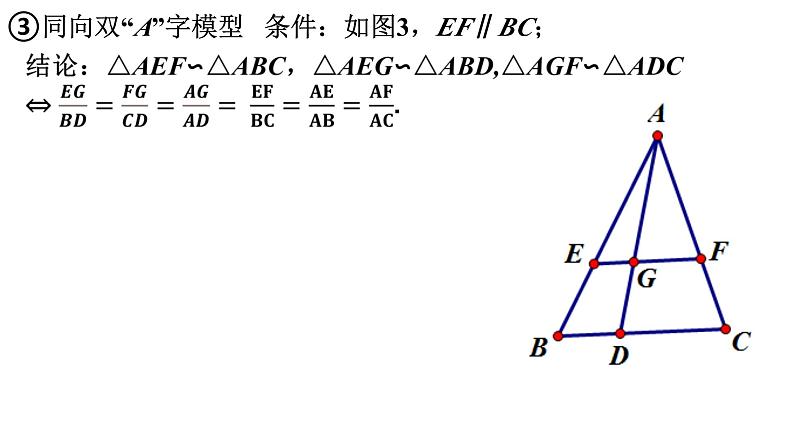
③同向双“A”字模型 条件:如图3,EF∥BC;
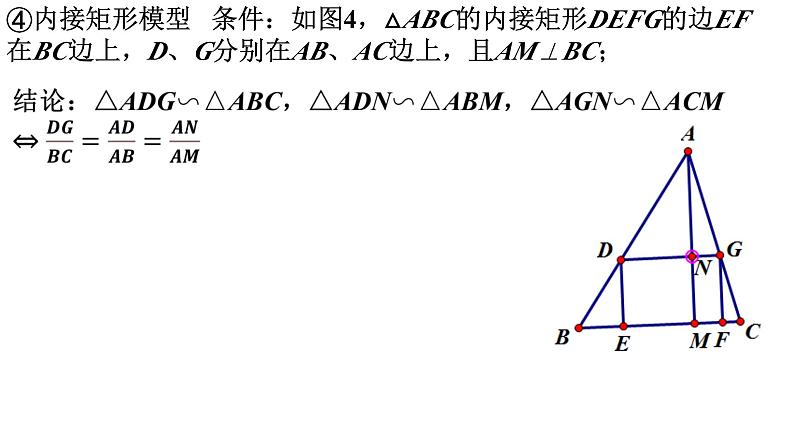
④内接矩形模型 条件:如图4,△ABC的内接矩形DEFG的边EF在BC边上,D、G分别在AB、AC边上,且AM⊥BC;
模型2.“X”字模型(“8”字模型)
模型3.“AX”字模型(“A8”字模型)
①一“A”+“8”模型 条件:如图1,DE∥BC;
②两”A”+“8”模型 条件:如图2,DE∥AF∥BC;
遇到飞鱼模型,常作平行线,其本质是构造8字型或者A字模型来解题.
飞鱼模型的特点:共顶点且过顶点的两条边共线
解决飞鱼模型的常见辅助线作法
注意:过点A与过点E的辅助线作法相同,过点D与过点B的辅助线作法也相同
如图,在△ABC中,点D,E分别在边BC,AC上,AE:CE=1:2,F是BE的中点,连接AF并延长交BC于点D,则BD:CD= ( )A.1:2 B.1:3 C.1:4 D.2:3
相似三角形模型之母子型相似
【知识储备】母子型相似证明题一般思路方法:①由线段乘积相等转化成线段比例式相等;②分子和分子组成一个三角形、分母和分母组成一个三角形;③第②步成立,直接从证这两个三角形相似,逆向证明到线段乘积相等;④第②步不成立,则选择替换掉线段比例式中的个别线段,之后再重复第③步。
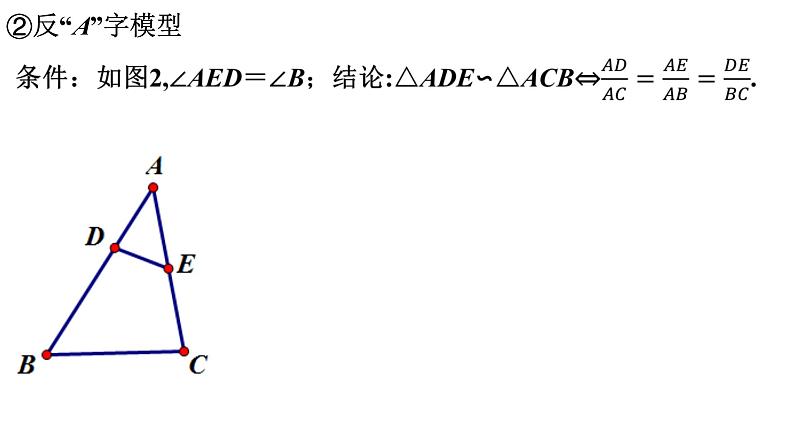
“母子”模型的图形(通常有一个公共顶点和另外一个不是公共的顶点,由于小三角形寓于大三角形中.恰似子依母怀),也是有一个“公共角”,再有一个角相等或夹这个公共角的两边对应成比例就可以判定这两个三角形相似.
1)“母子”模型(斜射影模型)条件:如图1,∠C=∠ABD; 结论:△ABD∽△ACB,AB2=AD·AC.
2)双垂直模型(射影模型)条件:如图2,∠ACB=90,CD⊥AB;结论:△ACD∽△ABC∽△CBD;CA2=AD·AB,BC2=BD·BA,CD2=DA·DB.
“手拉手”旋转型定义:如果将一个三角形绕着它的顶点旋转并放大或缩小(这个顶点不变),我们称这样的图形变换为旋转相似变换,这个顶点称为旋转相似中心,所得的三角形称为原三角形的旋转相似三角形。手拉手模型有以下特点:1)两个三角形相似;2)这两个三角形有公共顶点,且绕顶点旋转并缩放后2个三角形可以重合;3)图形是任意三角形(只要这两个三角形是相似的)。
相似模型之手拉手(旋转)模型
1)手拉手相似模型(任意三角形)
2)手拉手相似模型(直角三角形)
3)手拉手相似模型(特殊的等边三角形与等腰直角三角形)
模型1.对角互补模型(相似模型)
1)对角互补相似1条件:如图,在Rt△ABC中,∠C=∠EOF=90°,点O是AB的中点,
条件:如图,已知∠AOB=∠DCE=90°,∠BOC=α.
条件:已知如图,四边形ABCD中,∠B+∠D=180°。结论:如图,过点D作DE⊥BA,DF⊥BC,垂足分别为E、F;则:①△DAE∼△DCF;②A、B、C、D四点共圆。
模型.一线三等角模型(相似模型)
“一线三等角”型的图形,因为一条直线上有三个相等的角,一般就会有两个三角形的“一对角相等”,再利用平角为180°,三角形的内角和为180°,就可以得到两个三角形的另外一对角也相等(或利用外角定理也可),从而得到两个三角形相似.
1)一线三等角模型(同侧型)
条件:如图,∠1=∠2=∠3, 结论:△ACE∽△BED.横边×横边=竖边×竖边.
2)一线三等角模型(异侧型)
条件:如图,∠1=∠2=∠3, 结论:△ADE∽△BEC.
3)一线三等角模型(变异型)
①特殊中点型:条件:如图1,若C为AB的中点,且∠1=∠2=∠3,结论:△ACE∽△BED∽△ECD.
②一线三直角变异型1:条件:如图2,∠ABD=∠AFE=∠BDE=90°.结论:△ABC∽△BDE∽△BFC∽△AFB.
③一线三直角变异型2:条件:如图3,∠ABD=∠ACE=∠BDE=90°.结论:△ABM∽△NDE∽△NCM.
半角模型特征:①共端点的等线段; ②共顶点的倍半角;半角模型辅助线的作法:由旋转(或翻折)构造两对全等,从而将边转化,找到边与边的关系(将分散的条件集中,隐蔽的关系显现)。常见的考法包括:90°与45°(正方形、直角三角形);120°与60°(等边三角形)等。
1)半角模型(正方形(或等腰直角三角形)中的半角相似模型)条件:已知,如图,在正方形ABCD中,∠EAF的两边分别交BC、CD边于M、N两点,且∠EAF=45°
结论:如图1,△MDA∽△MAN∽△ABN;
条件:已知,如图,在正方形ABCD中,∠EAF的两边分别交BC、CD边于M、N两点,且∠EAF=45°结论:如图2,△BME∽△AMN∽△DFN.
条件:已知,如图,在正方形ABCD中,∠EAF的两边分别交BC、CD边于M、N两点,且∠EAF=45°
2)半角模型(含120-60°半角模型)
模型1.矩形中的十字架模型(相似模型)
矩形的十字架模型:矩形相对两边上的任意两点联结的线段是互相垂直的,此时这两条线段的的比等于矩形的两边之比。通过平移线段构造基本图形,再借助相似三角形和平行四边的性质求得线段间的比例关系。
模型2.等边三角形中的斜十字模型(相似模型)
条件:如图1,已知等边△ABC,BD=EC(或CD=AE),结论:①AD=BE,②AD和BE夹角为60°,③。
模型3.直角三角形中的十字模型(相似模型)
1)等腰直角三角形中的十字模型(全等+相似):
2)直角三角形中的十字模型:
梅涅劳斯(Menelaus,公元98年左右),是希腊数学家兼天文学家,梅涅劳斯定理是平面几何中的一个重要定理。塞瓦(G·Gev1647-1734)是意大利数学家兼水利工程师.他在1678年发表了一个著名的定理,后世以他的名字来命名,叫做塞瓦定理。使用梅涅劳斯和塞瓦定理可以进行直线形中线段长度比例的计算,其逆定理还可以用来进行三点共线、三线共点等问题的判定方法,是平面几何学以及射影几何学中的一项基本定理,具有重要的作用.
专题 相似模型之梅涅劳斯(定理)模型与塞瓦(定理)模型
模型1.梅涅劳斯(定理)模型及其逆定理
模型2.塞瓦(定理)模型
注意:塞(定理)的特征是三线共点,我们用塞瓦(定理)解决的大部分问题,也可添加辅助线后用平行线分线段成比例和相似来解决。
模型1.托勒密(定理)模型
模型2.托勒密不等式模型
相似三角形之圆幂定理模型口诀过一点引圆的切线或割线,那么这个点与圆的交点得到的线段的乘积是不变的,如果是切线的话,线段算两次,因此会有线段的平方.
如图,连接BD,BC,连接BO并延长与⊙O交于点E,连接CE. ∵AB是⊙O的切线,
∴ ∠ECB=90°.
∴ ∠CBE+ ∠CBA =90°.
∴ ∠CBA= ∠E
相关课件
这是一份2025年中考数学一轮复习课件之平行线与相交线模型,共17页。PPT课件主要包含了三线八角模型,三线八角动画显示,猪蹄模型M模型,模型讲解,铅笔头模型,锯齿模型,三角板拼接型等内容,欢迎下载使用。
这是一份数学中考第一轮复习微专题17 相似三角形之五大模型 课件,共40页。PPT课件主要包含了∠ACP,模型5对角互补型等内容,欢迎下载使用。
这是一份中考数学一轮复习 课件 微专题四 全等、相似三角形的进阶模型(K字型),共21页。PPT课件主要包含了第1题,模拟演练,第2题,第3题,第4题等内容,欢迎下载使用。









