2025年中考数学一轮教材复习-第七章 图形的变化 图形的对称、平移与旋转课件

这是一份2025年中考数学一轮教材复习-第七章 图形的变化 图形的对称、平移与旋转课件，共32页。PPT课件主要包含了教材知识复习，PART01，轴对称与中心对称，垂直平分，轴对称，中心对称，图形的折叠，∠ABC，∠BAC，∠BCA等内容，欢迎下载使用。
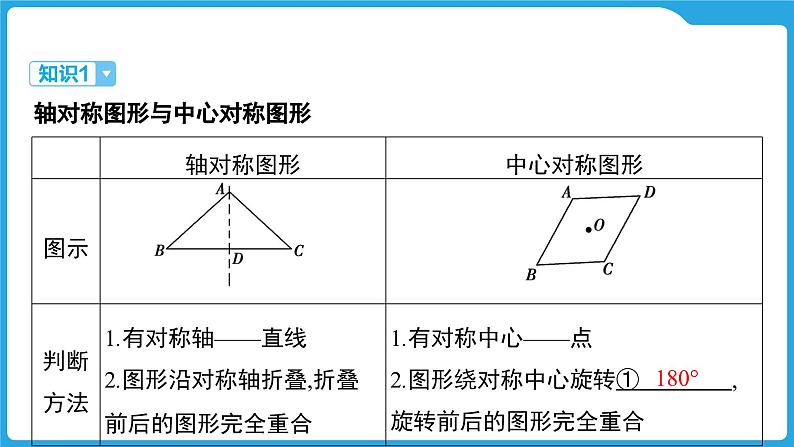
轴对称图形与中心对称图形
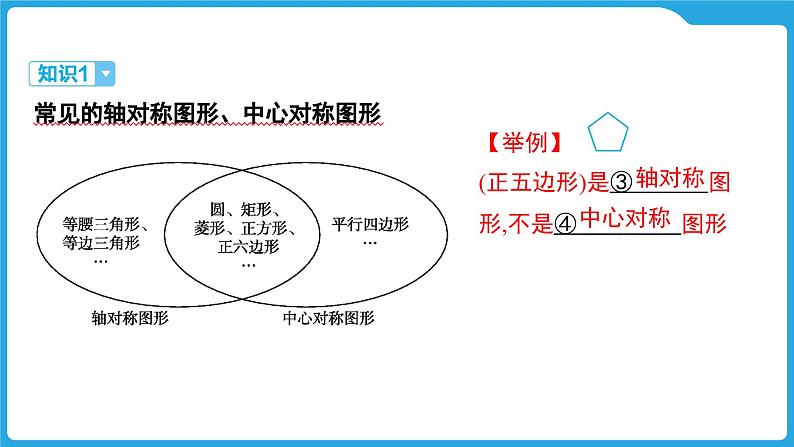
常见的轴对称图形、中心对称图形
【举例】(正五边形)是③　　　 图形,不是④　　 　图形 
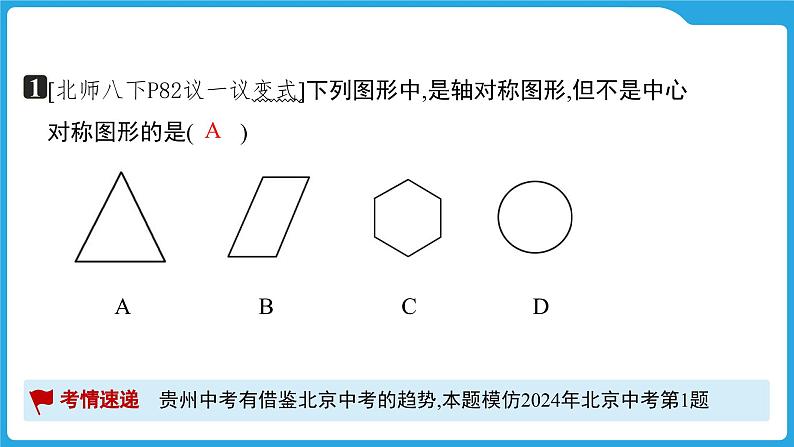
[北师八下P82议一议变式]下列图形中,是轴对称图形,但不是中心对称图形的是(　　)
A B C D
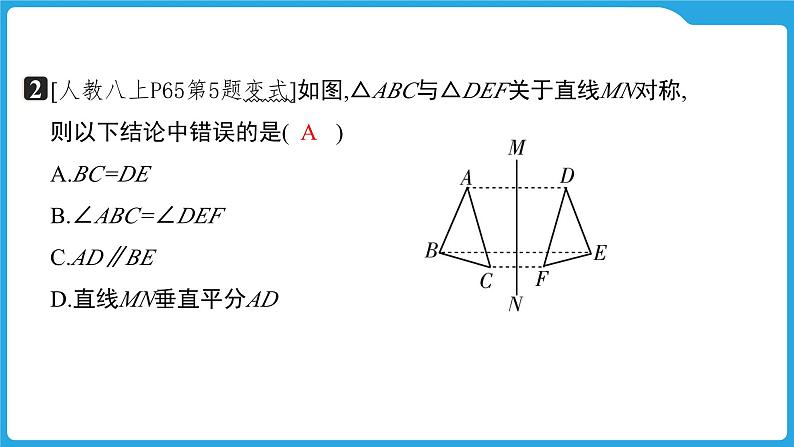
[人教八上P65第5题变式]如图,△ABC与△DEF关于直线MN对称,则以下结论中错误的是(　　)A.BC=DEB.∠ABC=∠DEFC.AD∥BED.直线MN垂直平分AD
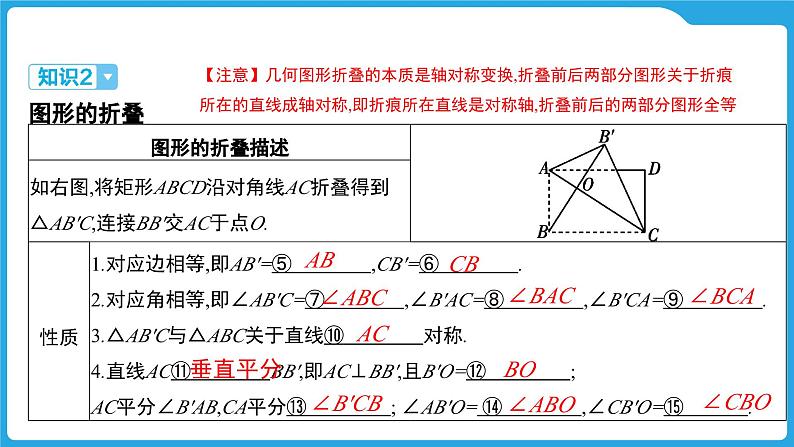
【注意】几何图形折叠的本质是轴对称变换,折叠前后两部分图形关于折痕所在的直线成轴对称,即折痕所在直线是对称轴,折叠前后的两部分图形全等
如图,在矩形ABCD中,M是边AB的中点,E是边BC上一点,连接AE,将△ABE沿着AE折叠得到△AFE,延长EF恰好经过点D.(1)在图中补全折叠后的△AFE.(2)由折叠得,AB=　　　　,BE=　　　　,∠ABE=∠　　　　,△ABE≌△　　　　. 
(1)补全图形如图（1）所示
(4)画出使PB+PM值最小时的点P，如图（2）所示
已知O为△ABC内一点,连接OA,OB,OC,将△BAO绕点B顺时针旋转后得到△BCD,连接OD.(1)如图(1),若△ABC为等边三角形,且OA=3,OB=4,OC=5.①∠OBD=　　　　°;②OD=　　　　;③∠BDC=　　　　°. 
(2)如图(2),若△ABC为等腰直角三角形,∠ABC=90°,AB=BC.①将△BAO绕点B顺时针旋转后得到△BDC,连接OD,根据题意在图(2)中画出图形,则∠OBD=　　　　°. ②若∠AOB=135°,OA=1,OB=2,求OC的长.(3)在(2)的条件下,求△ABC的面积.
①画出图形如图（3）所示
[2024贵州2题3分]“黔山秀水”写成下列字体,可以看作是轴对称图形的是(　　)
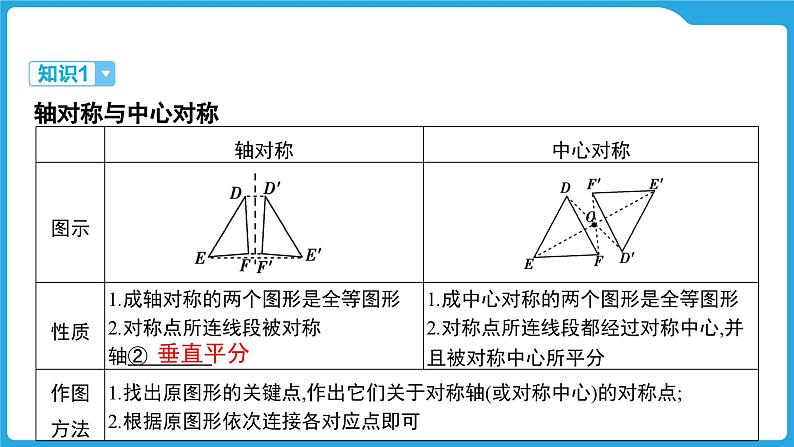
轴对称与中心对称(10年4考)
A B C D
[2024北京三帆中学模拟]剪纸是我国传统的民间艺术,下列剪纸作品中既是轴对称图形又是中心对称图形的是(　　)
[2024广安二模]如图,网格中每个小正方形的边长均为1,请你认真观察图(1)中三个网格中灰色部分构成的图案,解答下列问题.(1)图(1)中的三个图案都是　　　 对称图形,都不是　　　 对称图形.(填“中心”或“轴”) (2)在图(2)中选一个白色的小正方形涂灰,使图(2)中灰色部分构成的图案是轴对称图形.
[2017贵阳15题4分]如图,在矩形纸片ABCD中,AB=2,AD=3,点E是AB的中点,点F是AD边上的一个动点,将△AEF沿EF所在直线翻折,得到△A'EF,连接A'C,则A'C的长的最小值是　　　　. 
图形的折叠(10年3考)
[2024遵义播州区二模改编]如图,在菱形ABCD的DC边上有点E,连接AE,沿AE翻折△ADE,得到△AD'E,点D'恰好落在对角线AC上.若AB=4,∠DED'=90°,∠DAE=15°,则线段D'C的长为　　　　.
[2023贵州25题12分]如图(1),小红在学习了三角形相关知识后,对等腰直角三角形进行了探究,在等腰直角三角形ABC中,CA=CB,∠C=90°,过点B作射线BD⊥AB,垂足为B,点P在CB上.
图形的旋转(10年4考)
(1)【动手操作】如图(2),若点P在线段CB上,画出射线PA,并将射线PA绕点P逆时针旋转90°与BD交于点E,根据题意在图(2)中画出图形,∠PBE的度数为　　　　度. (2)【问题探究】根据(1)所画图形,探究线段PA与PE的数量关系,并说明理由.
(3)【拓展延伸】如图(3),若点P在射线CB上移动,将射线PA绕点P逆时针旋转90°与BD交于点E,探究线段BA,BP,BE之间的数量关系,并说明理由.
②当点P在线段CB的延长线上时,如图(4),连接AE,过点E作EF⊥CB,交CB的延长线于点F,∵△ABC是等腰直角三角形,∴∠ABC=45°,∴∠EBP=180°-∠CBE=45°.由(2)知A,B,P,E四点在以AE为直径的圆上,∴∠EAP=∠EBP=45°,∴∠AEP=90°-45°=45°,∴∠AEP=∠EAP,∴PA=PE.∵∠EFP=∠APE=90°,