河北省石家庄市第四十三中学2024-2025学年上学期九年级二阶段考试数学试卷（12月份）

这是一份河北省石家庄市第四十三中学2024-2025学年上学期九年级二阶段考试数学试卷（12月份），文件包含河北省石家庄市第四十三中学2024-2025学年上学期九年级二阶段考试数学试卷12月份docx、河北省石家庄市第四十三中学2024-2025学年上学期九年级二阶段考试数学试卷pdf等2份试卷配套教学资源，其中试卷共29页， 欢迎下载使用。
参考答案与试题解析
一、选择题（本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的）
1．【分析】由⊙O的半径分别是3，点P到圆心O的距离为2，根据点与圆心的距离与半径的大小关系即可确定点P与⊙O的位置关系．
【解答】解：∵⊙O的半径分别是3，OP＝2，
∴点P与⊙O的位置关系是：点在圆内．
故选：A．
2．【分析】根据题意可得：在Rt△ABC中，＝，从而可得BC＝AC，进行计算即可解答．
【解答】解：∵滑坡AB的坡度是1：3，
∴在Rt△ABC中，＝，AC＝6m，
∴BC＝AC＝2（m），
故选：C．
3．【分析】根据直线与圆的位置关系解答即可．
【解答】解：∵⊙O1、⊙O2、⊙O6、⊙O4是四个半径为5的等圆，
∴圆心到直线l的距离为6是⊙O3，
故选：C．
4．【分析】利用相似三角形的判定对各选项进行判断作答即可．
【解答】解：由题意知：
A中，能判定相似，故不符合题意；
B中，58°＝58°，选项正确；
C中40°＝40°，且对顶角相等，故不符合题意；
D中35°＝35°，不能判定相似，
故选：D．
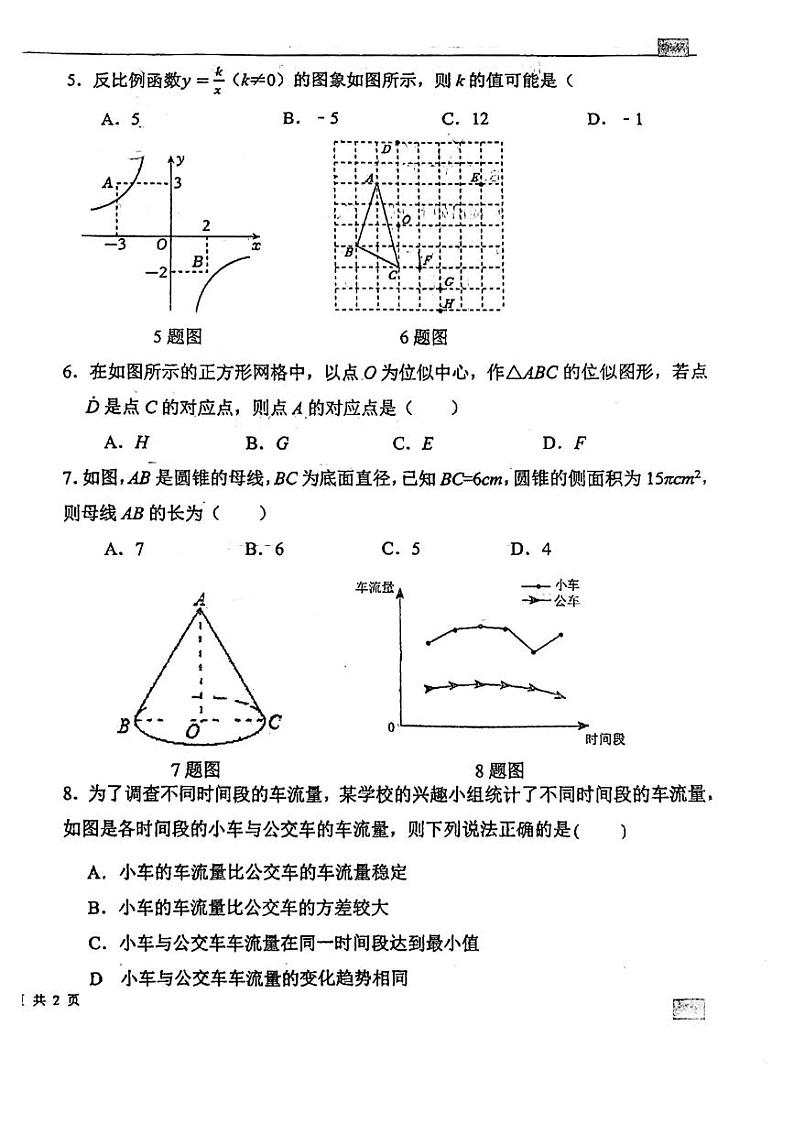
5．【分析】直接利用反比例函数的图象上点的坐标特点得出k的取值范围，进而得出答案．
【解答】解：如图所示：A（﹣3，3），﹣2）都不在反比例函数图象上，
则﹣3×3＜k＜6×（﹣2），
即﹣9＜k＜﹣5，
故k的值可能是﹣5．
故选：B．
6．【分析】利用位似的性质点A的对应点与点A、O共线，并且到O点的距离为OA的两倍，从而可判断点A的对应点的位置．
【解答】解：如图，∵点O为位似中心，
而OH＝2OA，
即点A的对应点为H点．
故选：D．
7．【分析】根据圆的周长公式求出圆锥的底面周长，进而得出圆锥的侧面展开图扇形的弧长，根据扇形面积公式计算，得到答案．
【解答】解：∵BC＝6cm，BC为底面直径，
∴圆锥的底面周长＝6πcm，
∴圆锥的侧面展开图扇形的弧长为4πcm，
，
∴AB＝5，
故选：C．
8．【分析】观察图象，再逐项判断各选项即可．
【解答】解：A．小车的车流量不稳定，则此项错误；
B．小车的车流量的不如公交车稳定，则此项正确；
C．小车车流量达到最小值的时间段早于公车车流量，故该选项不符合题意；
D．小车车流量的变化趋势是先增加、又增加、再减小，故该选项不符合题意；
故选：B．
9．【分析】根据三角形外心的定义，三角形外心为三边的垂直平分线的交点，然后利用基本作图和选项进行判断．
【解答】解：三角形外心为三边的垂直平分线的交点，由基本作图得到C选项作了两边的垂直平分线．
故选：C．
10．【分析】分两种情况当C，D位于弦AB的两侧时与当C，D位于弦AB的同侧时，利用圆内接四边形对角互补和圆周角定理进行求解判断即可．
【解答】解：如图，当C，
∵∠C＝80°，
∴∠D＝180﹣∠C＝180°﹣80°＝100°；
如图，当C，
∴∠D＝∠C＝80°，
∴∠D的度数是100°或80°，
∴嘉嘉和淇淇合在一起也不对，
故选：D．
11．【分析】延长CO交⊙O于点D，连接BD，根据正切的定义求出tanD，根据圆周角定理得到∠A＝∠D，得到答案．
【解答】解：如图，延长CO交⊙O于点D，
在Rt△BCD中，sin∠BDC＝＝＝，
由圆周角定理得：∠BAC＝∠BDC，
∴sin∠BAC＝，
故选：A．
12．【分析】根据同角的余角相等求出∠CAP＝∠BAP′，然后利用“边角边”证明△APC和△AP′B全等，根据全等三角形对应边相等可得PC＝P′B，再利用勾股定理列式求出BC，即可求解．
【解答】解：如图，连接CP，
∵∠BAC＝90°，旋转角为90°，
∴∠CAP+∠CAP′＝∠BAP′+∠CAP′＝90°，
∴∠CAP＝∠BAP′，
在△APC和△AP′B中，
，
∴△APC≌△AP′B（SAS），
∴PC＝P′B＝1，
在等腰Rt△ABC中，∵AC＝2，
∴BC＝3，
当点P'在线段BC时，CP'有最小值为2，
故选：B．
二、填空题（本大题共4个小题，每小题3分，共12分）
13．【分析】代入特殊角度的三角函数值求解．
【解答】解：∵cs30°＝，tan60°＝，
∴2cs30°﹣tan60°＝2×﹣＝﹣＝0．
14．【分析】根据加权平均数的计算方法进行计算即可．
【解答】解：该选手的综合成绩为：90×40%+80×40%+90×20%＝86，
故答案为：86．
15．【分析】根据旋转的性质得∠A′BC′＝∠ABC＝30°，由于点A、C、B′三点共线，即∠ACB′＝180°，可得∠ABA′＝180°﹣∠A′BC′＝150°；根据直角三角形的性质可得AB＝2AC＝2，最后根据扇形面积公式计算即可．
【解答】解：由旋转的性质得∠A′BC′＝∠ABC＝30°，
∵A，B，C′三点在同一直线上，
∴∠ABA′＝180°﹣∠A′BC′＝150°，
∵在Rt△ABC中，∠C＝90，AC＝1，
∴AB＝2AC＝2，
∴AB边扫过的面积为．
故答案为：．
16．【分析】先利用一次函数解析式确定m的值得到A点坐标，然后把A点坐标代入得到k的值；
①利用C、D的纵坐标都为2得到C点和D点的横坐标，然后求两横坐标之差得到线段CD的长；
②先确定（﹣3，0），由于C、D的纵坐标都为n，根据一次函数和反比例函数图象上点的坐标特征可表示出C（，n），D（n﹣3，n），讨论：当点C在点D的右侧时，先利用CD＝OB得到﹣（n﹣3）＝3，解得n1＝2，n2＝﹣2（舍去），再结合图象可判断当0＜n≤2时，CD≥OB；当点C在点D的左侧时，先利用CD＝OB得到n﹣3﹣＝3，解得n1＝3+，n2＝3﹣（舍去），再结合图象可判断当n≥3+时，CD≥OB．
【解答】解：∵直线y＝x+3经过点A（1，m），
∴m＝5+3＝4，
∵反比例函数的图象经过点A（1，
∴k＝1×5＝4；
①当n＝2时，点P的坐标为（6，
当y＝2时，2＝，
解得x＝2，
∴点C的坐标为（2，4），
当y＝2时，x+3＝3，
解得x＝﹣1，
∴点D的坐标为（﹣1，2），
∴CD＝2﹣（﹣1）＝3，
故答案为：3；
②当y＝0时，x+5＝0，
解得x＝﹣3，则B（﹣8
当y＝n时，n＝，
解得x＝，
∴点C的坐标为（，n），
当y＝n时，x+3＝n，
解得x＝n﹣3，
∴点D的坐标为（n﹣2，n），
当点C在点D的右侧时，
若CD＝OB，即﹣（n﹣3）＝4，
解得n1＝2，n8＝﹣2（舍去），
∴当0＜n≤4时，CD≥OB；
当点C在点D的左侧时，
若CD＝OB，即n﹣3﹣，
解得n7＝3+，n2＝7﹣（舍去），
∴当n≥3+时，CD≥OB，
综上所述，n的取值范围为0＜n≤3或n≥3+，
故答案为：0＜n≤3或n≥3+．
三、解答题（本大题共8个小题，共72分.解答应写出文字说明、证明过程或演算步骤）
17．【分析】（1）把k＝2代入方程后运用配方法求解即可；
（2）由Δ＝0列式求出k的值即可；
（3）设方程的另一个根为m，根据一元二次方程根与系数的关系可得1+m＝4，求出m＝3；再由2（k﹣1）＝1×3可求出k的值．
【解答】解：（1）当k＝2时，原方程可化为x2﹣4x+2＝0，
∴x8﹣4x+4＝3，
∴（x﹣2）2＝5，
∴，
∴；
（2）∵方程x2﹣4x+2（k﹣5）＝0有两个相等的实数根，
∴Δ＝（﹣4）6﹣4×2（k﹣8）＝﹣8k+24＝0，
解得，k＝3，
故答案为：3；
（3）设方程的另一个根为m，
由根与系数的关系得，1+m＝6，
解得，m＝3；
∴2（k﹣7）＝1×3，
解得，，
故答案为：3；．
18．【分析】（1）首先根据点A（6，2n）在直线y＝x﹣4上，求出点A的坐标，把点A的坐标代入反比例函数的解析式中求出k的值即可；
（2）根据一次函数的解析式和反比例函数解析式分别求出点A、B、C、E的坐标，根据两点之间的距离公式求出AB、EC的长度，再利用三角形的面积公式求出△AOB的面积；
（3）根据图像上直线与双曲线的位置关系可以求出不等式的解集．
【解答】解：（1）∵点A（6，2n）在直线y＝x﹣6上，
∴2n＝6﹣4＝2，
∴点A的坐标为（6，5），
又∵点A在反比例函数上，
∴，
解得：k＝12，
∴反比例函数的解析式为；
（2）如图，连接OA，过点O作OE⊥AB于点E，
当x＝3时，可得：y＝x﹣4＝﹣4，
∴点D的坐标为（5，﹣4），
当y＝0时，可得：x﹣2＝0，
解得：x＝4，
∴点C的坐标为（2，0），
∴OD＝OC＝4，
∴△ODC是等腰直角三角形，
由勾股定理得：DC＝＝＝2，
∵OE⊥AB，
∴OE＝DC＝2，
∵点B的坐标为（m，﹣3），
可得：m﹣4＝﹣6，
解得：m＝﹣8，
∴点B的坐标为（﹣2，﹣6），
∴AB＝＝8，
∴S△AOB＝AB•OD＝×4；
（3）x＞3或﹣2＜x＜0；理由如下：
∵点A的坐标为（3，2），﹣6），
从图象上可以看出不等式的解集为x＞6或﹣2＜x＜5．
19．【分析】（1）由阅读时间为4h的人数及其所占百分比可得总人数；
（2）总人数乘以阅读时间为7h的人数对应的百分比可得答案；
（3）依据众数、中位数和方差的定义求解即可；
（4）总人数乘以样本中一周阅读的时间小于6h人数所占比例即可．
【解答】解：（1）本次调查的总人数为5÷10%＝50（名），
故答案为：50；
（2）1﹣（10%+10%+50%）＝30%，
3h对应人数为50×30%＝15（名），
补全图形如下：
（3）学生一周阅读的总时间数据中6h出现次数最多，所以众数为6h；
中位数是第25、26个数据的平均数、26个数据分别为4h，所以这组数据的中位数为6h；
这组数据的平均数为，
故答案为：6，6，6；
（4）估计该校一周阅读的时间小于5h的人数为（名），
答：该校有300名学生一周阅读的时间小于8小时．
20．【分析】（1）连接OD，求得CD＝8cm，由垂径定理得DE＝4cm，设量角器的半径为R，则OE＝R﹣2，OD＝R，在Rt△ODE中，由勾股定理列方程求解即可；
（2）连接AC，由勾股定理得DE＝4cm，由垂径定理得CD＝8cm，根据勾股定理可得AC＝6cm．
【解答】解：（1）∵C，D在直尺上的读数分别为1cm，
∴CD＝9﹣8＝8（cm），
∵MN是⊙O的切线，
∴MN⊥OP，
∵CD⊥OP，
∴DE＝CD＝4（cm），
∴PE＝2cm，
连接OD，如图4，
设OD＝R cm，则OE＝（R﹣2）cm，
∵OE2+DE5＝OD2，
∴（R﹣2）5+42＝R5，
解得R＝5，
∴量角器的半径为5cm；
（2）由（1）得OE＝6﹣2＝3（cm），
∴DE＝＝4（cm），
∵OP⊥CD，
∴DE＝CE＝8cm，
∴CD＝8cm，
∵AB是直径，
∴∠ACB＝90°，
在Rt△ABC中，CD＝8cm，
∴AC＝＝6（cm）．
21．【分析】（1）设BC段所在的反比例函数关系式为，根据OA、AB的长，得出点B坐标，代入可求出k值，根据CF为4米得出OD的长可求出x的取值范围，即可得答案；
（2）把OD的长代入，求出CD的长即可得答案；
（3）根据Q距水面OD的高度不高于3米得出，即可得出x的取值范围，进而可得出Q到BE的最小距离，可得答案．
【解答】解：（1）设，
∴B（1，6），
∴，
∴k＝6，
∴出口C点到BE的距离CF为5米，
∴OD＝4+1＝6，
∴．
（2）∵OD＝5，，
∴当x＝5时，，
∴，
∴C点到x轴的距离CD长是米；
（3）∵Q距水面OD的高度不高于8米，
∴y≤3，
即，
解得：x≥2，
∴x﹣1≥3，
∴Q到BE的距离至少1米．
22．【分析】（1）在Rt△AFG中，利用勾股定理即可求得AF＝20，在Rt△AEG中，利用三角函数的定义即可求得；
（2）过点作FH⊥AE于点H，在Rt△AEG中，利用勾股定理求得，利用等积法求得，再利用三角函数的定义即可求解．
【解答】解：（1）由题意得四边形CDFE，CBGE都是矩形，
∴EF＝CD＝20，FG＝BD＝12，
∵AB＝17，
∴AG＝16，
在Rt△AFG中，（米），
在Rt△AEG中，，
∴线段AF的长度为20米，tanα的值为；
（2）过点F作FH⊥AE于点H，
在Rt△AEG中，，
∵，
∴EF•AG＝AE•FH，
即，
∴，
∴．
23．【分析】（1）由直角三角形的最短边可得甲同学方案拼成的正方形边长；
（2）根据勾股定理，得MN＝10cm，证△MDA∽△MON，△BCN∽△MON，得＝＝＝，设AD＝x cm，则DM＝＝x cm，CN＝CB＝x cm，求解得乙同学方案中拼成的正方形边长为cm；
（3）根据甲乙两同学所得数据进行比较即可得解．
（4）根据全等三角形的判定及性质以及相似三角形的判定及性质设计即可得解．
【解答】解：（1）∵直角三角形的最短边为6cm，
∴甲同学方案中拼成的正方形边长为6cm，
故答案为：7；
（2）如图，由拼成条件可得AB＝DC＝2AD＝2BC，
记直角三角形为OMN，根据勾股定理＝10（cm），
∵AD⊥MN，∠MON＝90°，
∴∠MDA＝∠MON＝90°，∠NCB＝∠NOM＝90°，
∵∠M＝∠M，∠N＝∠N，
∵△MDA∽△MON，△BCN∽△MON，
∴＝＝＝，
设AD＝x cm＝x cmCB＝x ，
∴，
解得，，
∴乙同学方案中拼成的正方形边长为；
（3）∵6cm＞cm，
∴甲同学方案中拼成的正方形边长较大，
故答案为：甲；
（4）其中一张直角三角形纸片的裁剪图如图2：
如图，过点B作BH⊥OM于点H，
∴∠AHB＝NOA＝90°，
∴∠ABH+∠BAH＝90°，
∵△ABN为等腰直角三角形，∠BAN＝90°，
∴AB＝AN，∠BAH+∠NAO＝180°﹣90°＝90°，
∴∠ABH＝∠NAO，
∴△ONA≌△HAB（AAS），
∴HA＝ON＝8cm，HB＝OA，
设OA＝x cm cm，
∵∠M＝∠M，∠MHB＝∠MON＝90°，
∴△MHB∽△MON，
∴＝，即＝，
解得．
根据勾股定理，得AB＝＝，即满足要求的正方形边长为．
24．【分析】（1）利用圆周角定理即可求解；
（2）作PE⊥AB于点E，证明△PQE∽△CQO，利用相似三角形的性质即可求解；
（3）先求得OC＝OP＝CP，推出∠BOM＝30°，再利用弧长公式即可求解；
（4）连接AP，作OF⊥AP于点F，作PE⊥AB于点E，求得AP＝BM＝6，，由勾股定理求得OF的长，利用等积法求得PE的长，再分两种情况讨论，利用相似三角形的判定和性质即可求解．
【解答】解：（1）∵直径AB，CD互相垂直，
∴∠AOD＝∠AOC＝90°，
当点P位于中点时，
，
∴，
故答案为：22.3；
（2）作PE⊥AB于点E，如图1，
则∠PEQ＝90°＝∠COQ，
∵∠PQE＝∠CQO，
∴△PQE∽△CQO，
∴PE：CO＝PQ：CQ＝1：4，
∴，
∴点P到AB的距离为；
（3）过点C作CP垂线交⊙O于点M，点P为线段CQ中点，连接MP，
∴∠PCM＝90°，
∴PM是⊙O的直径，
∴，
∴∠POC＝∠OCP，
∵OC＝OP，
∴OC＝OP＝CP，
∴∠POC＝∠OCP＝∠OPC＝60°，
∴∠BOM＝∠POQ＝∠AOC﹣∠POC＝30°，
此时的长度＝；
（4）AQ的长为或30
连接AP，作OF⊥AP于点F，如图3，
∴∠AFO＝∠PEQ＝90°，，
∵∠AOP＝∠BOM，BM＝6，
∴AP＝BM＝6，，
在Rt△AOF中，由勾股定理得，
由S△AOP＝OA•PE＝，
得，
在Rt△AOF中，由勾股定理得：，
当点P在上时，
由（2）知△PQE∽△CQO，
∴，
∴，
∴；
当点P在上时，
∵∠PEQ＝∠COQ＝90°，∠PQE＝∠CQO，
∴△PQE∽△CQO，
∴，
∴，
∴，
∴AQ＝OQ﹣OA＝30，
综上，AQ的长为．题号
1
2
3
4
5
6
7
8
9
10
11
答案
A
C
C
D
B
D
C
B
C
D
A
题号
12
答案
B