苏科版（2024）七年级上册（2024）6.2 角示范课ppt课件

这是一份苏科版（2024）七年级上册（2024）6.2 角示范课ppt课件，共31页。PPT课件主要包含了小于和等于，角平分线等内容，欢迎下载使用。
如果已知两个角的度数，我们可以通过度数来比较角的大小． 如果不知道两个角的度数，那么如何来确定它们之间的大小关系呢？
回忆：我们已经学习了比较两条线段的长短，有哪些方法呢？ 会有哪些比较结果？
观察法，度量法，叠合法；
归纳：如果不知道两个角的度数,也可以通过观察法、 叠合法进行比较.
有一张长方形纸片（图6-7），如何比较相邻两条边 AB，AD 的长短？
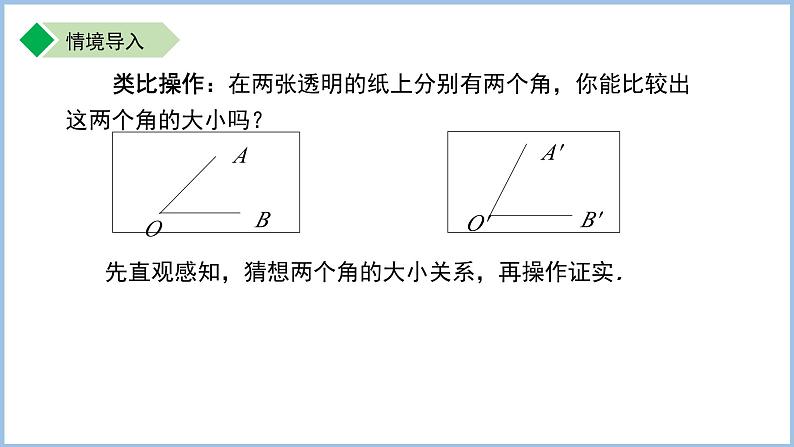
先直观感知，猜想两个角的大小关系，再操作证实．
类比操作：在两张透明的纸上分别有两个角，你能比较出这两个角的大小吗？
将∠AOB平移到∠A′O′B′的位置，使得点O与点O′重合，射线OB与射线O′B′重合，看射线OA的位置．若射线OA落在∠A′O′B′内部，则∠AOB小于∠A′O′B′；若射线OA落在∠A′O′B′外部，则∠AOB大于∠A′O′B′；若射线OA与O′A′重合，则∠AOB等于∠A′O′B′．
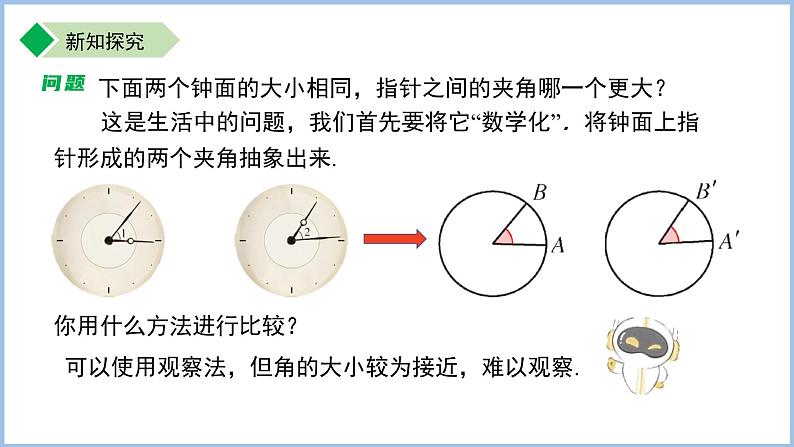
下面两个钟面的大小相同，指针之间的夹角哪一个更大？
这是生活中的问题，我们首先要将它“数学化”．将钟面上指针形成的两个夹角抽象出来.
你用什么方法进行比较？
可以使用观察法，但角的大小较为接近，难以观察.
可以使用叠合的方法比较大小.
可以使用度量的方法比较大小. 如：测量角度.
可以使用度量的方法比较大小.又或通过测量AB、A′B长短比较两个角张开的程度.
根据角的定义，角可以看成是一条射线绕着它的端点旋转到另一个位置所成的图形．∠AOB可以看成是OB从OA出发，绕点O按逆时针方向旋转形成的．当点A、B之间的距离确定时，∠AOB的大小也随之确定.
使用这种方式动手试一试.
归纳：可以比较AB与A′B′的长短，来判断两个角的大小．当AB＞A′B′时，∠AOB＞∠A′O′B′；当AB＜A′B′时，∠AOB＜∠A′O′B′；当AB＝A′B′时，∠AOB＝∠A′O′B′；角的大小转化为线段的长短比较.
用叠合法比较两个角大小的过程，相当于作一个角等于已知角.利用以上的思路，我们可以用直尺和圆规作一个角等于已知角.
在透明纸上画一个角，把这个角对折，使角的两边重合，再展开纸片．
折痕把这个角分成的两个角相等吗？你是怎么发现的？
答：相等，使用度量法、叠合法、转化法
这条折痕所在的射线在数学中叫做“角平分线”.在学线段时，我们知道，如果一个点把一条线段分成相等的条线段，那么这个点叫作这条线段的中点．你能类比“中点”的概念描述它吗？
如果从角的顶点出发的一条射线把这个角分成两个相等的角，这条射线叫作这个角的平分线．
类比线段中点，角平分线的定义可以进行两方面的判断和表述：
如果OC是∠AOB的平分线，那么∠AOC＝∠BOC＝ ∠AOB,或∠AOB＝2∠AOC＝2∠BOC.
反之，如果OC是∠AOB内的一条射线，且∠AOC＝∠BOC，或∠AOC＝ ∠AOB，或∠BOC＝ ∠AOB，或∠AOB＝2∠AOC，或∠AOB＝2∠BOC，那么OC是∠AOB的平分线．
如图，射线OC从∠AOB的边OA出发，绕点O向边OB旋转，∠1和∠2的大小关系发生了怎样的变化？
（1）∠1与∠2在动态变化时，当一个角在变化时，另一个角随之而改变，在比较大小时要注意分类讨论．但是∠1与∠2在变化时，也有不变的量，你发现了吗？
答：∠1与∠2的和不变．
（2）如果∠1与∠2的和是80°，如何分类讨论，比较两个角的大小？
答：∠1∠2.
对于任意的∠α和∠β，下列三种关系有且只有一种成立：∠α＜∠β，∠α＝∠β，∠α＞∠β．
如图，已知∠AOB，作∠A'O′B′，使∠A′O′B′＝∠AOB．
尺规作图作法：（1）以点O为圆心，任意长为半径作弧，交OA，OB于点C，D．
（2）作射线O′A′．以点O′为圆心，OC长为半径作弧PQ，交O′A′于点C′．
（3）以点C′为圆心，CD长为半径作弧，交弧PQ于点D′．
（4）过点O′，D′作射线O′B′，∠A′O′B′即为所求作的角．
如图，∠AOD＝80°，OC是∠AOD内的一条射线，OB是∠AOC的平分线，∠AOB＝30°．求∠AOC和∠COD的度数.
解：因为OB是∠AOC的平分线，∠AOB＝30°， 所以∠AOC＝2∠AOB＝2×30°＝60°. 又因为∠COD＝∠AOD－∠AOC， ∠AOD＝80°， 所以∠COD＝80°－60°＝20°.
1.下列说法中正确的有（　　）①过两点有且只有一条直线；②连接两点的线段叫两点的距离；③两点之间线段最短；④若AB＝BC，则点B是AC的中点；⑤把一个角分成两个角的射线叫角的平分线；⑥直线l经过点A，那么点A在直线l上．A．2个 B．3个 C．4个 D．5个
√ ×√ × × √
2.如图所示，已知点O是直线CD上的一点，∠AOC＝30°，OB平分∠AOD，则∠BOD的度数是（　 ）
A．75° B．65° C．55° D．45°
3.如图，O是直线AB上一点，过O作任意射线OM，OC平分∠AOM， OD平分∠BOM，则∠COD的度数是（　　）
A．80° B．90° C．100° D．不能确定
4.如图，OC是∠AOD的平分线，OE是∠BOD的平分线，∠AOB＝130°．（1）求∠COE的度数是多少？（2）如果∠COD＝20°，求∠BOE的度数．