福建省龙岩市长汀县2024-2025学年上学期期中九年级数学试卷 （原卷版）-A4

这是一份福建省龙岩市长汀县2024-2025学年上学期期中九年级数学试卷 （原卷版）-A4，共6页。试卷主要包含了选择题，填空，解答题等内容，欢迎下载使用。
（考试时间：120分钟；满分150分）
一、选择题（每小题4分，共40分）
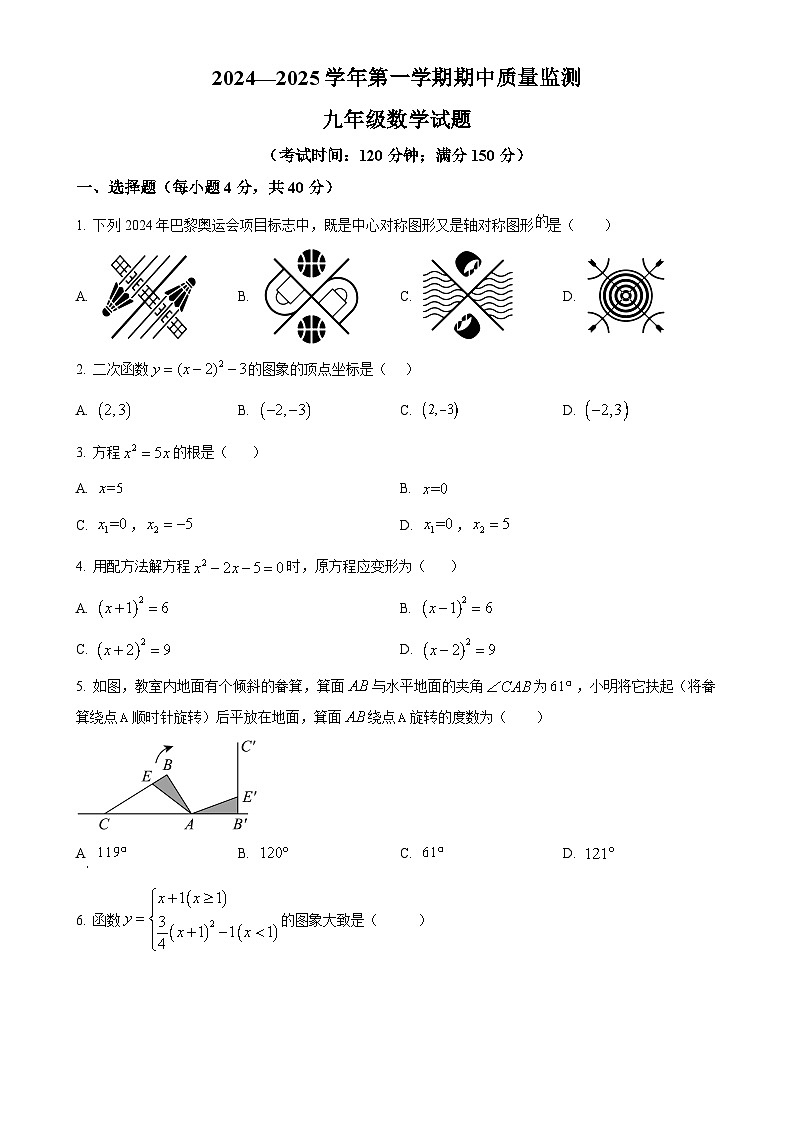
1. 下列2024年巴黎奥运会项目标志中，既是中心对称图形又是轴对称图形是（ ）
A. B. C. D.
2. 二次函数的图象的顶点坐标是（ ）
A. B. C. D.
3. 方程的根是（ ）
A. B.
C. ，D. ，
4. 用配方法解方程时，原方程应变形为（ ）
A. B.
C. D.
5. 如图，教室内地面有个倾斜的畚箕，箕面与水平地面的夹角为，小明将它扶起（将畚箕绕点顺时针旋转）后平放在地面，箕面绕点旋转的度数为（ ）

A B. C. D.
6. 函数的图象大致是（ ）
A. B. C. D.
7. 如图，中，，将绕点顺时针旋转得到，点的对应点分别为，延长交于点，下列结论一定正确的是（ ）
A. B.
C D.
8. 二次函数的部分图象如图所示，其对称轴为直线，且与x轴的一个交点坐标为．下列结论：；；；关于的一元二次方程有两个不相等的实数根．其中正确结论的个数是（ ）

A. 个B. 个C. 个D. 个
9. 《九章算术》中有这样一道题：“今有二人同所立．甲行率六，乙行率四．乙东行，甲南行十步而邪东北与乙会．问：甲、乙行各几何？”大意是说：已知甲、乙二人同时从同一地点出发，甲速度为6，乙的速度为4．乙一直向东走，甲先向南走10步，后又斜向北偏东方向走了一段后与乙相遇．那么相遇时，甲走了多少步（ ）
A. 24B. 30C. 32D. 36
10. 在平面直角坐标系中，点为坐标原点，抛物线与轴交于点，与轴正半轴交于点，连接，将向右上方平移，得到，且点，落在抛物线的对称轴上，点落在抛物线上，则直线的表达式为（ ）
A. B. C. D.
二、填空（本大题共6题，每题4分，共24分）
11. 若是一元二次方程的一个根，则_______．
12. 已知：点与点关于原点成中心对称，则________．
13. 将抛物线先向右平移个单位长度，再向下平移个单位长度，平移后的抛物线的解析式为 _________________．
14. 如图，将绕直角顶点逆时针旋转得到，若，则__．
15. 若关于的一元二次方程无实数根，则整数的最大值为______．
16. 若一个点的纵坐标是横坐标的3倍，则称这个点为“三倍点”，如：，，等都是“三倍点”．在的范围内，若二次函数的图象上有且只有一个“三倍点”，则c的取值范围是________．
三、解答题（本大题共9小题，共86分）
17. 用合适方法解以下方程．
（1）
（2）
18. 关于的方程有两个不等的实数根．
（1）求的取值范围；
（2）化简：．
19. 定义：如果一元二次方程满足，那么我们称这个方程为“凤凰”方程．已知是“凤凰”方程，且有两个相等的实数根，求的值．
20. 在直角坐标系中，，．
（1）画出线段关于轴的对称线段AB；
（2）将线段CA绕点顺时针旋转一个角，得到对应的线段CD，使得轴，请画出线段CD；
（3）若直线平分四边形的面积，请求出的值．
21. 如图，在平面直角坐标系中，点的坐标为，等边经过平移或轴对称或旋转都可以得到．
（1）沿轴向右平移得到，则平移的距离是______个单位长度；与关于直线对称，则对称轴是______；绕原点顺时针旋转得到，则旋转角度可以是______度．
（2）连接，交于点，求的长．
22. 如图，△ADE由△ABC绕点A按逆时针方向旋转90°得到，且点B的对应点D恰好落在BC的延长线上，AD，EC相交于点P．
（1）求∠BDE的度数；
（2）F是EC延长线上的点，且∠CDF＝∠DAC．判断DF和PF的数量关系，并证明．
23. 根据下列要求，解答相关问题．
（1）请补全以下求不等式的解集的过程．
①构造函数，画出图象：根据不等式特征构造二次函数；并在下面的坐标系中（见图1）画出二次函数的图象（只画出图象即可）．
②借助图象，写出解集：由所标示图象，可得不等式的解集为______．
（2）利用（1）中求不等式解集的步骤，求不等式的解集．
①构造函数，画出图象；②求得界点，标示所需；③借助图像，写出解集．
24. 请根据以下素材，完成探究任务．
25. 如图，已知抛物线经过原点O和x轴上另一点A，它的对称轴与x轴交于点C，直线经过抛物线上一点，且与y轴．直线分别交于点D、E．
（1）求m的值及该抛物线对应的函数关系式；
（2）①判断的形状，并说明理由；②判断与的位置关系；
制定加工方案
生产背景
背景1
◆某民族服装厂安排70名工人加工一批夏季服装，有“风”“雅”“正”三种样式．
◆因工艺需要，每位工人每天可加工且只能加工“风”服装2件，或“雅”服装1件，或“正”服装1件．
◆要求全厂每天加工“雅”服装至少10件，“正”服装总件数和“风”服装相等.
背景2
每天加工的服装都能销售出去，扣除各种成本，服装厂的获利情况为：
①“风”服装：24元/件；
②“正”服装：48元/件；
③“雅”服装：当每天加工10件时，每件获利100元；如果每天多加工1件，那么平均每件获利将减少2元．
信息整理
现安排x名工人加工“雅”服装，y名工人加工“风”服装，列表如下：
服装种类
加工人数（人）
每人每天加工量（件）
平均每件获利（元）
风
y
2
24
雅
x
1
正
1
48
探究任务
任务1
探寻变量关系
求x、y之间的数量关系．
任务2
建立数学模型
设该工厂每天的总利润为w元，求w关于x的函数表达式．
任务3
拟定加工方案
制定使每天总利润最大的加工方案．