2021~2022学年山东省青岛市市北区八年级(上)期末数学试卷(解析版)

这是一份2021~2022学年山东省青岛市市北区八年级(上)期末数学试卷(解析版)，共11页。试卷主要包含了选择题，填空题，作图题，解答题等内容，欢迎下载使用。
一、选择题（共有8道小题，下列每小题都给出标号为A、B、C、D的四个结论，其中只有一个是正确的．每小题选得分；不选、选错或选出的标号超过一个的不得分）
1. 下列各数中的无理数是（ ）
A. 2022B. C. D. π
【答案】D
【解析】A．2022是有理数，故此选项不符合题意；
B．是有理数，故此选项不符合题意；
C．是有理数，故此选项不符合题意；
D．π是无理数，故此选项符合题意；
故选：D．
2. 在方差计算公式s2[（x1﹣15）2+（x2﹣15）2+…+（x20﹣15）2]中，可以看出15表示这组数据的（ ）
A. 众数B. 平均数C. 中位数D. 方差
【答案】B
【解析】在方差计算公式s2= [（x1-15）2+（x2-15）2+…+（x20-15）2]中，数15表示这组数据的平均数；
故选：B．
3. 下列命题中，真命题有（ ）
（1）如果一个数的算术平方根等于它本身，则这个数是1；
（2）一个数的立方根等于它本身，则这个数是﹣1，0，1；
（3）同一平面内，过一点有且只有一条直线与已知直线垂直；
（4）在同一平面内，垂直于同一直线的两条直线互相平行．
A. 1个B. 2个C. 3个D. 4个
【答案】C
【解析】（1）如果一个数的算术平方根等于它本身，那么这个数是0或1，所以（1）为假命题；
（2）一个数的立方根等于它本身，则这个数是-1，0，1，所以（2）为真命题；
（3）在同一平面内，过一点有且只有一条直线与已知直线垂直，所以（3）为真命题；
（4）在同一平面内，垂直于同一直线的两条直线互相平行，所以（4）为真命题．
综上，（2）（3）（4）三个正确，
故选：C．
4. 如果点A(﹣3，y1)和B(2，y2)都在直线yx﹣b上，则y1与y2的大小关系是（ ）
A. y1＞y2B. y1＜y2C. y1＝y2D. 不确定
【答案】A
【解析】∵k=-＜0，
∴y随x的增大而减小，
又∵点A（-3，y1）和B（2，y2）都在直线y=-x-b上，且-3＜2，
∴y1＞y2．
故选：A．
5. 如图，是可调躺椅示意图，AE与BD的交点为C，且，，保持不变．为了舒适，需调整的大小，使．根据图中数据信息，下列调整大小的方法正确的是（ ）
A. 增大10°B. 减小10°
C. 增大15°D. 减小15°
【答案】B
【解析】如图，延长，交于点，
∵∠ACB = 180°-50° –60° = 70°
∴∠ECD = ∠ACB = 70°
∵∠DGF = ∠DCE ＋∠E
∴∠DGF = 70° + 30° = 100°，
∵∠EFD= 110°,
∠EFD =∠DGF ＋∠D，
∴∠D= 10°，
而图中∠D＝20°，
∴∠D应减少10°，
故选B．
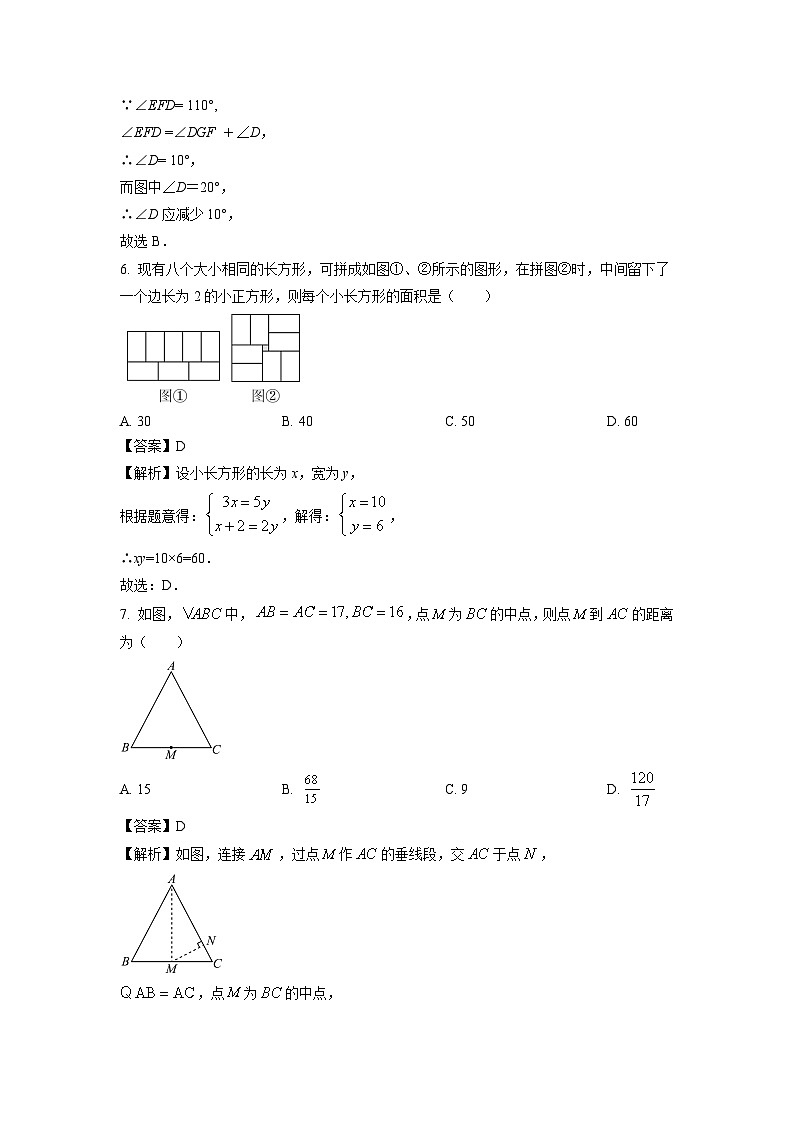
6. 现有八个大小相同的长方形，可拼成如图①、②所示的图形，在拼图②时，中间留下了一个边长为2的小正方形，则每个小长方形的面积是（ ）

A. 30B. 40C. 50D. 60
【答案】D
【解析】设小长方形的长为x，宽为y，
根据题意得：，解得：，
∴xy=10×6=60．
故选：D．
7. 如图，中，，点为的中点，则点到的距离为（ ）

A. 15B. C. 9D.
【答案】D
【解析】如图，连接，过点作的垂线段，交于点，

，点为的中点，
且，
，
，
，
即点到的距离，
故答案为：D．
8. 在一次自行车越野赛中，出发m小时后，小明骑行了25km，小刚骑行了18km，此后两人分别以akm/h和bkm/h匀速骑行，他们骑行的时间t（单位：h）与骑行的路程s（单位：km）之间的函数关系如图所示，观察图象，下列说法中正确的有（ ）
①出发m小时内小明的速度比小刚快；②a＝26；③小刚追上小明时离起点43km；④此次越野赛的全程为90km．
A. 1个B. 2个C. 3个D. 4个
【答案】C
【解析】由图象可知，
出发mh内小明的速度比小刚快，故①正确；
由图象可得，，解得，，
故②正确；
小刚追上小明走过的路程是：36×（0.5+0.7）=36×1.2=43.2km＞43km，故③错误；
此次越野赛的全程是：36×（0.5+2）=36×2.5=90km，故④正确；
故选：C．
二、填空题（共6道小题）
9. 在平面直角坐标系中，点(a2+1，﹣1)一定在第_____象限．
【答案】四
【解析】∵a2≥0，
∴a2+1＞0，
∴点（a2+1，-1）一定在第四象限．
故答案为：四．
10. 比较大小：________（选填“＞”、“=”、“＜”）．
【答案】＞
【解析】∵=＞，
故答案为：＞．
11. 一副直角三角板如图放置，∠F=∠ACB=90°，点C在FD的延长线上，∠E=45°，∠A=60°，AB∥CF，则∠DBC的度数为_____度．
【答案】15
【解析】∵∠F=∠ACB=90°，∠E=45°，∠A=60°，∴∠EDF=45°，∠ABC=30°．
∵AB∥CF，∴∠EDF=∠ABD=45°．∴∠DBC=∠ABD-∠ABC=45°-30°=15°．
12. 已知直线y＝2x与y＝﹣x+b的交点为(﹣1，a)，则方程组的解为____．
【答案】
【解析】把（-1，a）代入y=2x得a=-2，
则直线y=2x与y=-x+b的交点为（-1，-2），
则方程组的解为 ．
13. 如图所示，已知四边形ABCD是等边长为2的正方形，AP=AC，则数轴上点P所表示的数是________．
【答案】1﹣2
【解析】根据勾股定理，可得AC==2，根据数轴上两点间的距离AP=AC=2，可得P点坐标1﹣2．
14. 如图，某学校（A点）到公路（直线l）的距离为300米，到公交车站（D点）的距离为500米，现要在公路边上建一个商店（C点），使之到学校A及到车站D的距离相等，则商店C与车站D之间的距离是____米．
【答案】312.5
【解析】过点A作AB⊥l于B，
则AB=300，AD=500．
∴BD==400，
设CD=x，则CB=（400-x），
根据勾股定理得：x2=（400-x）2+3002，
整理得：x2=160000+x2-800x+3002，
解得：x=312.5．
答：商店与车站之间的距离为312.5米，
故答案为：312.5．
三、作图题
15. 在如图所示的正方形网格中，每个小正方形的边长为1，格点三角形（顶点是网格线的交点的三角形）ABC的顶点A，C的坐标分别为（﹣4，5），（﹣1，3）．
（1）请在如图所示的网格平面内作出平面直角坐标系；
（2）请作出△ABC关于y轴对称的△A1B1C1．
解：（1）（2）如图；
四、解答题（本题共8道小题）
16. 计算：
（1）2；
（2）（3）（3）+3．
解：（1）；
（2）
．
17. 解方程组：
（1）；
（2）．
解：（1），
②×2-①得-7y=-14，
y=2，
把y=2代入②得，x=8，
∴此方程组的解为；
（2）原方程组可化为
①×4-②×3得7x=42，
x=6，
把x=6代入①得y=4，
∴此方程组的解为．
18. 某长途汽车客运站规定，乘客可以免费携带一定质量的行李，但超过该质量则需购买行李票，且行李费y（元）是行李质量x（千克）的一次函数，现已知李明带了60千克的行李费，交了行李费5元；张华带了90千克的行李，交了行李费10元．
（1）写出y与x之间的函数表达式．
（2）旅客最多可免费携带多少千克的行李？
解：（1）设行李费y（元）关于行李质量x（千克）的一次函数关系式为y=kx+b
由题意得，解得k=，b=-5
∴该一次函数关系式为y=x-5
（2）∵x-5≤0，解得：x≤30，
∴旅客最多可免费携带30千克的行李．
19. 某校为了解木校学生参与学校号召的“周末公益”活动的情况．随机调查了部分本校学生．根据调查结果，绘制出如图的统计图．请根据图①和图②的相关信息，解答下列问题：
（1）本次接受调查的初中学生人数为 人，图①中m的值为 ；
（2）求统计的这部分学生参加周末公益时间的平均数、众数和中位数．
解：（1）4÷10%=40（人），
×100%=25%，即m=25，
故答案为：40，25；
（2）样本平均数为：0.9×10%+1.2×20%+1.5×37.5%+1.8×25%+2.1×7.5%=1.5（h），
样本中出现次数最多的是1.5h，共用15次，因此众数是1.5h，
将这40人参加公益活动时间从小到大排列，处在中间位置的两个数都是1.5h，因此中位数是1.5h，
答：平均数是1.5h，中位数是1.5h，众数是1.5h．
20. 某商场购进甲、乙两种服装后，都加价再标价出售，春节期间商场搞优惠促销，决定将甲、乙两种服装分别按标价的八折和九折出售，某顾客购买甲、乙两种服装共付款元，两种服装标价之和为元，这两种服装的进价和标价各是多少元？
解：设甲的进价为x元，乙的进价为y元，依题意得：
，
解得，
．
答：甲、乙进价分别为50元、100元，标价分别为70元、140元．
21. 如图，已知，，求证：．

证明：，，，
，，
又，，．
22. 甲、乙两名同学沿直线进行登山，甲、乙沿相同的路线同时从山脚出发到达山顶．甲同学到达山顶休息1小时后再沿原路下山，他们离山脚的距离S（千米）随时间t（小时）变化的图象如图所示，根据图象中的有关信息回答下列问题：
（1）甲同学上山过程中S甲与t的函数解析式为 ；乙同学上山过程中S乙与t的函数解析式为 ；点D的坐标为 ；
（2）若甲同学下山时在点F处与乙同学相遇，此时点F与山顶的距离为0.75千米；
①求甲同学下山过程中S与t的函数解析式；
②相遇后甲、乙各自继续下山和上山，求当乙到达山顶时，甲与乙的距离是多少千米．
解：（1）设甲、乙两同学登山过程中，路程s（千米）与时间t（时）函数解析式分别为S甲=k1t，S乙=k2t，
由图象得2=4k1，2=6k2，
∴k1=，k2=，
∴解析式分别为S甲=t，S乙=t；
当S甲=4时，t=8，
∴甲到达山顶时间是8小时，而甲同学到达山顶休息1小时后再沿原路下山，
∴D（9，4），
故答案为：S甲=t，S乙=t，（9，4）；
（2）①当y=4-0.75=时，t=，
解得t=，
∴点F（，），
设甲同学下山过程中S与t的函数解析式为S=kt+b，将D（9，4）和F（，）代入得：，解答，
∴甲同学下山过程中S与t的函数解析式为S=-t+13；
②乙到山顶所用时间为：4÷=12（小时），
当x=12时，S=-12+13=1，
当乙到山顶时，甲离乙的距离是：4-1=3（千米）．
答：当乙到达山顶时，甲与乙的距离是3千米．
23. 如图，一次函数的图象过、两点，与轴交于点．
（1）求此一次函数的解析式；
（2）求的面积；
（3）已知：点在轴上，且使的值最小，请直接写出点的坐标______，及的最小值是______．
解：（1）根据题意得， 解得，
此一次函数的解析式为；
（2）当时，，解得，则，
；
（3）作点关于轴的对称点，连接交轴于点，连接，如图，
，，
此时的值最小，最小值为，
设直线的解析式为，
把，分别代入得，解得，
直线的解析式为，
当时，，解得，点的坐标为．