山东省新高考联合质量测评2022-2023学年高一下学期3月联考数学试题（学生版）

这是一份山东省新高考联合质量测评2022-2023学年高一下学期3月联考数学试题（学生版），共6页。
考试用时120分钟，满分150分
注意事项：
1．答题前，考生先将自己的学校、班级、姓名、考号、座号填涂在相应位置．
2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑．如需改动，用橡皮擦干净后，再选涂其他答案标号．回答非选择题时，将答案写在答题卡上．写在本试卷上无效．
3．考试结束，考生必须将试题卷和答题卡一并交回．
一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．
1. 若，，则终边所在象限为( )
A. 第一象限B. 第一、三象限C. 第二象限D. 第二、四象限
2. 若是直线上的一个单位向量，，，则向量在直线l上的坐标为( )
A. B. C. 3D. 1
3. 已知向量，，，若，则实数m的值是( )
A －10B. －8C. 10D. 8
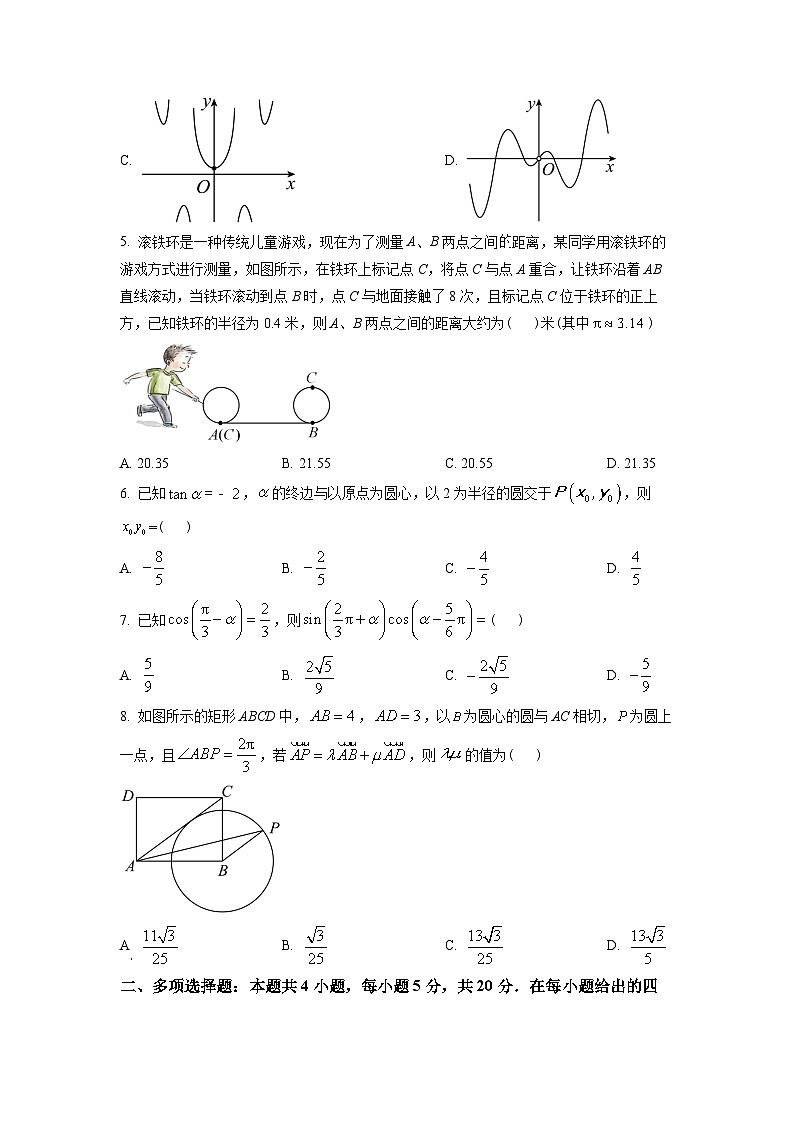
4. 函数的部分图象可能是( )
A.
B.
C. D.
5. 滚铁环是一种传统儿童游戏，现在为了测量A、B两点之间距离，某同学用滚铁环的游戏方式进行测量，如图所示，在铁环上标记点C，将点C与点A重合，让铁环沿着AB直线滚动，当铁环滚动到点B时，点C与地面接触了8次，且标记点C位于铁环的正上方，已知铁环的半径为0.4米，则A、B两点之间的距离大约为( )米(其中)
A. 20.35B. 21.55C. 20.55D. 21.35
6. 已知，的终边与以原点为圆心，以2为半径的圆交于，则=( )
A. B. C. D.
7. 已知，则( )
A. B. C. D.
8. 如图所示的矩形ABCD中，，，以为圆心的圆与AC相切，为圆上一点，且，若，则的值为( )
A B. C. D.
二、多项选择题：本题共4小题，每小题5分，共20分．在每小题给出的四个选项中，有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分．
9. 已知，，则( )
A. B. C. D.
10. 已知点在角的终边上，且，则的值可以是( )
A. B. C. D. 0
11. 已知平面上点是直线外一点，是直线上给定的两点，点是直线上的动点，且满足，则下列说法正确的是( )
A. 当时，点C为线段的中点B. 当点C为线段的三等分点时，
C. 当时，点C在线段上D. 当点C在线段的延长线上时，
12. “奔驰定理”因其几何表示酷似奔驰的标志得来，是平面向量中一个非常优美的结论．奔驰定理与三角形四心(重心、内心、外心、垂心)有着神秘的关联．它的具体内容是：已知M是内一点，，，的面积分别为，，，且．以下命题正确的有( )
A. 若，则为的重心
B. 若为的内心，则
C. 若，，为的外心，则
D. 若为的垂心，，则
三、填空题：本题共4小题，每小题5分，共20分．
13. 已知为坐标原点，，，则______．
14. ______．
15. 在平面直角坐标系中，点与点关于原点对称，则的一个取值为______．
16. 如图所示，点是平行四边形BCDE内(含边界)的一点，点B是AC的中点，，且．
①当时，______；
②的最大值为______．
四、解答题：本题共6小题，共70分.解答应写出文字说明，证明过程或演算步骤．
17. 如图，点A，B，C是圆上点．
(1)若，，求扇形AOB的面积和弧AB的长；
(2)若扇形AOB面积为，求扇形AOB周长的最小值，并求出此时的值．
18. 设，，．
(1)当t=4时，将用和表示；
(2)若A，B，C三点能构成三角形，求实数t应满足的条件．
19. 如图矩形ABCD，，，AC与EF交于点N．
(1)若，求的值；
(2)设，，试用，表示．
20. 潍坊市“渤海之眼”摩天轮是吉尼斯世界纪录认证的“世界最高的无轴摩天轮”，横跨白浪河，采用桥梁与摩天轮相结合的形式建设，高度145米，直径125米，拥有36个悬挂式观景仓，绕行一周用时30分钟，它的最低点D离地面20米.摩天轮圆周上一点A从过圆心O1与地面平行的位置开始旋转，逆时针运动t分钟后到达点B，设点B与地面的距离为h米．
(1)求函数的关系式；
(2)用五点法作图，画出函数，的图象．
21. 已知函数的部分图像如图所示．
(1)求函数的解析式，并求出该函数的单调递增区间；
(2)将函数的图像向左平移个单位长度，再把横坐标变为原来的2倍(纵坐标不变)，得到函数的图像，求的解析式；
(3)若在上恒成立，求实数的取值范围．
22. 如图一：球面上的任意两个与球心不在同一条直线上的点和球心确定一个平面，该平面与球相交的图形称为球的大圆，任意两点都可以用大圆上的劣弧进行连接.过球面一点的两个大圆弧，分别在弧所在的两个半圆内作公共直径的垂线，两条垂线的夹角称为这两个弧的夹角.如图二：现给出球面上三个点，其任意两个不与球心共线，将它们两两用大圆上的劣弧连起来的封闭图形称为球面三角形.两点间的弧长定义为球面三角形的边长，两个弧的夹角定义为球面三角形的角.现设图二球面三角形的三边长为，，，三个角大小为，，，球的半径为.
(1)求证：
(2)①求球面三角形的面积(用，，，表示).
②证明：.