北师大版（2024）八年级下册第六章 平行四边形3 三角形的中位线公开课教学ppt课件

这是一份北师大版（2024）八年级下册第六章 平行四边形3 三角形的中位线公开课教学ppt课件，共19页。PPT课件主要包含了剪拼法，添辅助线，证三角形全等，证明平行四边形，得出结论，补短加倍，取中截长，三角形，平行四边形，证明方法等内容，欢迎下载使用。
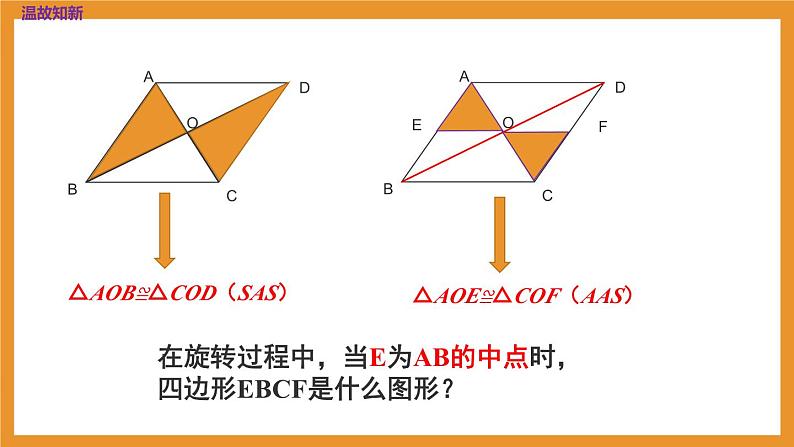
△AOB≌△COD（SAS）
△AOE≌△COF（AAS）
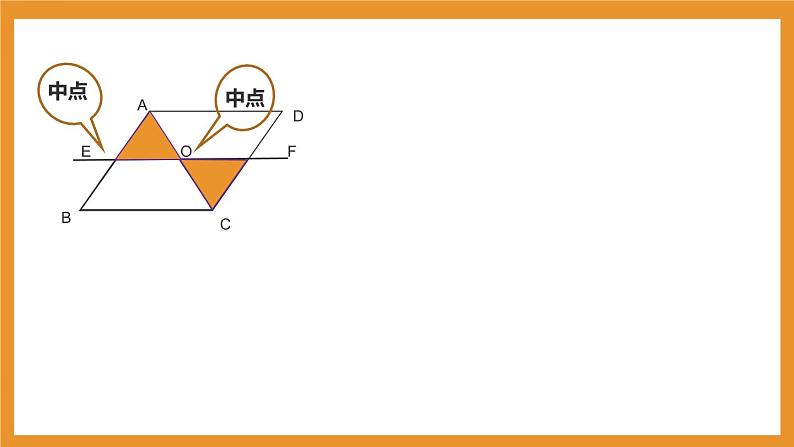
在旋转过程中，当E为AB的中点时，四边形EBCF是什么图形？
《课程标准》: 要求“探索并证明三角形的中位线定理．”
根据《课程标准》，确定本节课的学习目标为：（1）通过回顾旧知的探究操作，能自主总结出三角形中位线的定义，发展几何直观；（2）通过独立思考与小组合作等方式，经历三角形中位线定理的形成过程，能够对三角形的中位线定理进行证明，体会转化的数学思想，发展逻辑推理能力；（3）能运用三角形的中位线定理解决简单的实际问题，提高应用意识.
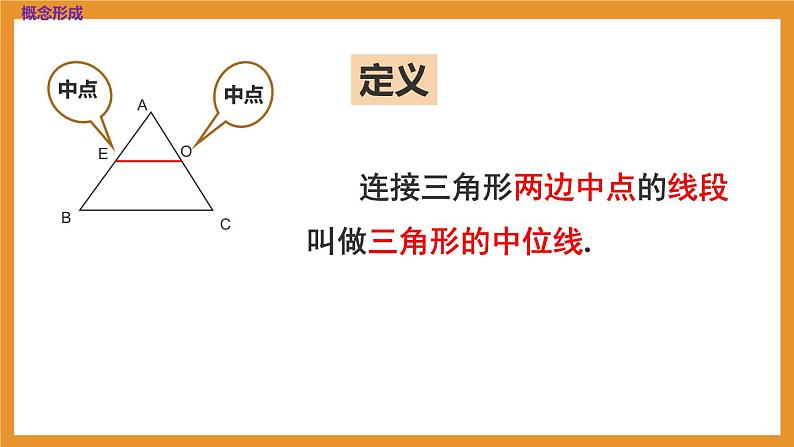
连接三角形两边中点的线段叫做三角形的中位线.
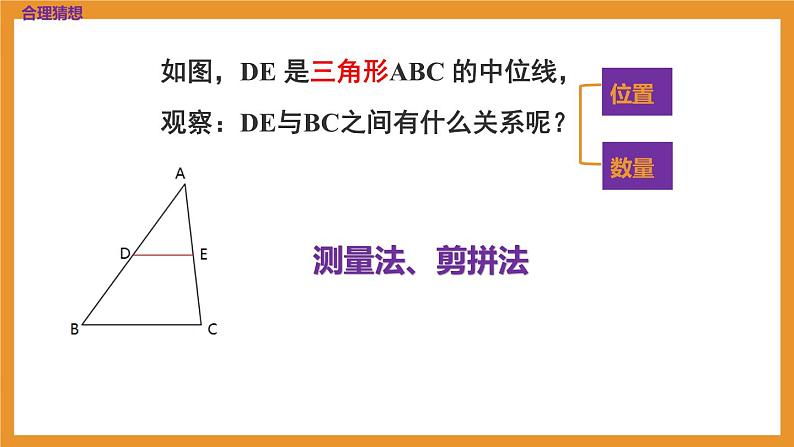
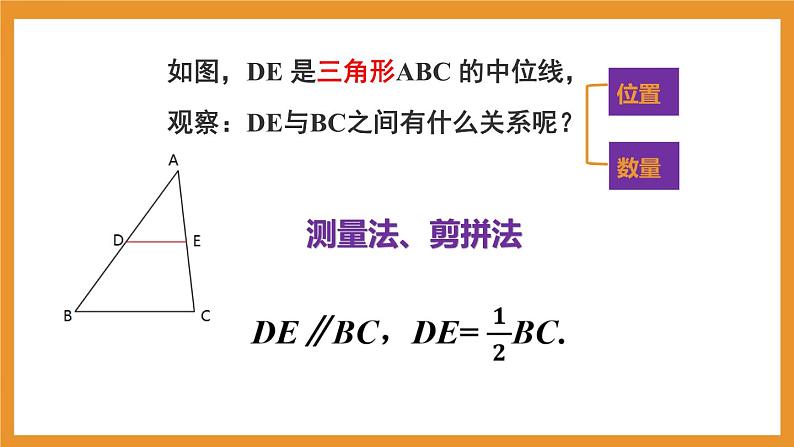
如图，DE 是三角形ABC 的中位线，
观察：DE与BC之间有什么关系呢？
* 测量法 *
小组同学各自标出自己所剪的三角形的三个顶点字母A、B、C，并找出边AB，BC的中点，作出中位线DE.（1）沿中位线剪开，将剪开后的两部分拼一拼。（2）对照拼成的图形，讨论交流，猜想结果.
* 剪拼法 *
小组同学各自标出自己所画的三角形的三个顶点字母A、B、C，并找出边AB，BC的中点，作出中位线DE.（1）度量线段DE和BC的长度.（2）度量∠ADE和∠B的度数.将测量结果填写在给定的表格里，猜想结果.
活动要求：四人小组，根据学习活动单上的活动步骤，任选一种方法完成探索。
问题：你还有其他证明方法吗？
三角形的中位线平行于三角形的第三边， 且等于第三边的一半；
三角形的中位线定理：
在我国古代数学名著《九章算术注》中，刘徽通过割补的方法推导三角形面积公式，从三角形面积公式的推导过程中也隐含了证明三角形中位线性质的方法。
一题多证，你发现这些解法有什么共同特点吗？
例题 如图，在平面内任意画一个四边形ABCD，以四边的中点为顶点组成一个新四边形EFGH，我们称这个新四边形EFGH为中点四边形.
问：（1）四边形EFGH 的周长与谁有何关系？
（2）四边形EFGH 是什么图形？
1．如图所示，Rt△ABC中，∠C＝90°，BC＝6，AC＝8，D、E分别为AC、BC的中点，连接DE，则DE长为（　　）A．4B．5C．6D．7
2．如图，BD是△ABC的中线，E、F分别是BD，BC的中点，连接EF，若EF＝2，则AD的长为（　　）A．2B．3C．4D．5
3．如图，Rt△ABC中，∠C＝90°，∠B＝35°．D，E，F分别是边AB，BC，AC的中点，则∠DEF的度数是 　 　．
4. 如图，平行四边形ABCD的对角线AC，BD相交于点O， AE=EB，若∠ADC=70°，求∠AEO的度数.
解：∵四边形ABCD是平行四边形, ∴AO=OC，∠ABC=∠ADC=70°. ∵AE=EB， ∴OE//BC . ∴∠AEO=∠ABC=70°.
1.本节课我们学习了哪些内容？
2.我们经历了怎样的过程来发现中位线定理，又是怎么证明这个定理呢？
3.为什么中位线的学习安排在平行四边形这一章节的最后，你有什么启发？
利用三角形研究平行四边形
从平行四边形中探究三角形
基础作业：课本152页第1，2题提高作业：课本152页第3题实践作业：
请你尝试使用本节课学习过的知识，写出解决下面这个问题的测量方案吧！