高二数学上学期期末复习选择题压轴题二十三大题型专练（范围：第一、二、三章）

这是一份高二数学上学期期末复习选择题压轴题二十三大题型专练（范围：第一、二、三章），文件包含高二上学期期末复习选择题压轴题二十三大题型专练范围第一二三章原卷版docx、高二上学期期末复习选择题压轴题二十三大题型专练范围第一二三章解析版docx等2份试卷配套教学资源，其中试卷共95页， 欢迎下载使用。
题型1
向量共线、共面的判定及应用
1．（24-25高二上·陕西西安·开学考试）在下列条件中，使M与A，B，C一定共面的是（ ）
A．OM=OA−OB−OC
B．OM=15OA+13OB+12OC
C．MA+MB+MC=0
D．OM+OA+OB+OC=0
2．（23-24高二上·新疆伊犁·期末）已知e1、e2、e3为空间三个不共面的向量，向量a=e1+μe2+4e3，b=3e1+9e2+λe3，若a与b共线，则λ+μ=（ ）
A．−3B．3C．−15D．15
3．（23-24高二上·江西九江·期末）对于空间任一点O和不共线的三点A，B，C，有OP→=xOA→+yOB→+zOC→，则x+y+z=1是P，A，B，C四点共面的（ ）
A．必要不充分条件B．充分不必要条件
C．充要条件D．既不充分又不必要条件
4．（23-24高二上·全国·课后作业）在下列条件中，使M与A，B，C不一定共面的是（ ）
A．OM=3OA−2OB−OCB．OM+OA+OB+OC=0
C．MA+MB+MC=0D．OM=14OB−OA+12OC
题型2
空间向量的数量积问题
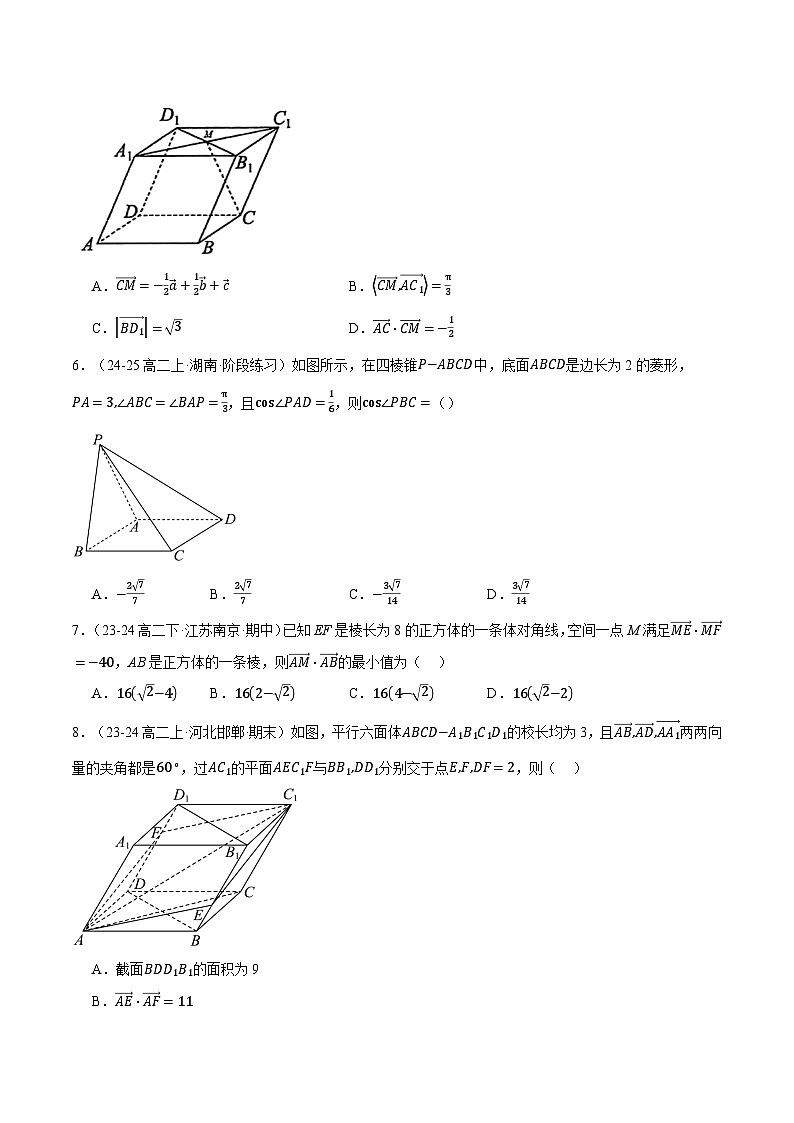
5．（24-25高二上·黑龙江大庆·阶段练习）如图，在平行六面体ABCD−A1B1C1D1中，AB=AD=AA1=1，∠BAD=∠DAA1=∠BAA1=π3，M为A1C1与B1C1的交点，若AB=a，AD=b，AA1=c，下列说法正确的是（ ）
A．CM=−12a+12b+cB．CM,AC1=π3
C．BD1=3D．AC⋅CM=−12
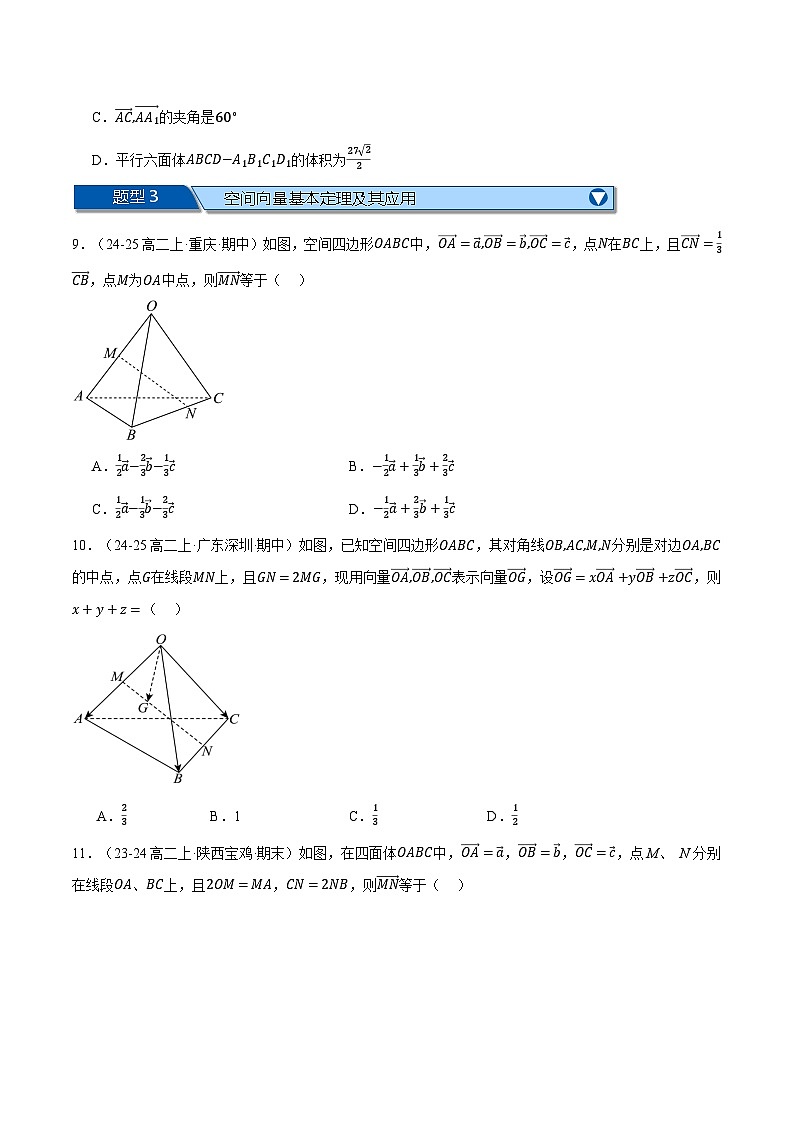
6．（24-25高二上·湖南·阶段练习）如图所示，在四棱锥P−ABCD中，底面ABCD是边长为2的菱形，PA=3,∠ABC=∠BAP=π3，且cs∠PAD=16，则cs∠PBC=（）
A．−277B．277C．−3714D．3714
7．（23-24高二下·江苏南京·期中）已知EF是棱长为8的正方体的一条体对角线，空间一点M满足ME⋅MF=−40，AB是正方体的一条棱，则AM⋅AB的最小值为（ ）
A．162−4B．162−2C．164−2D．162−2
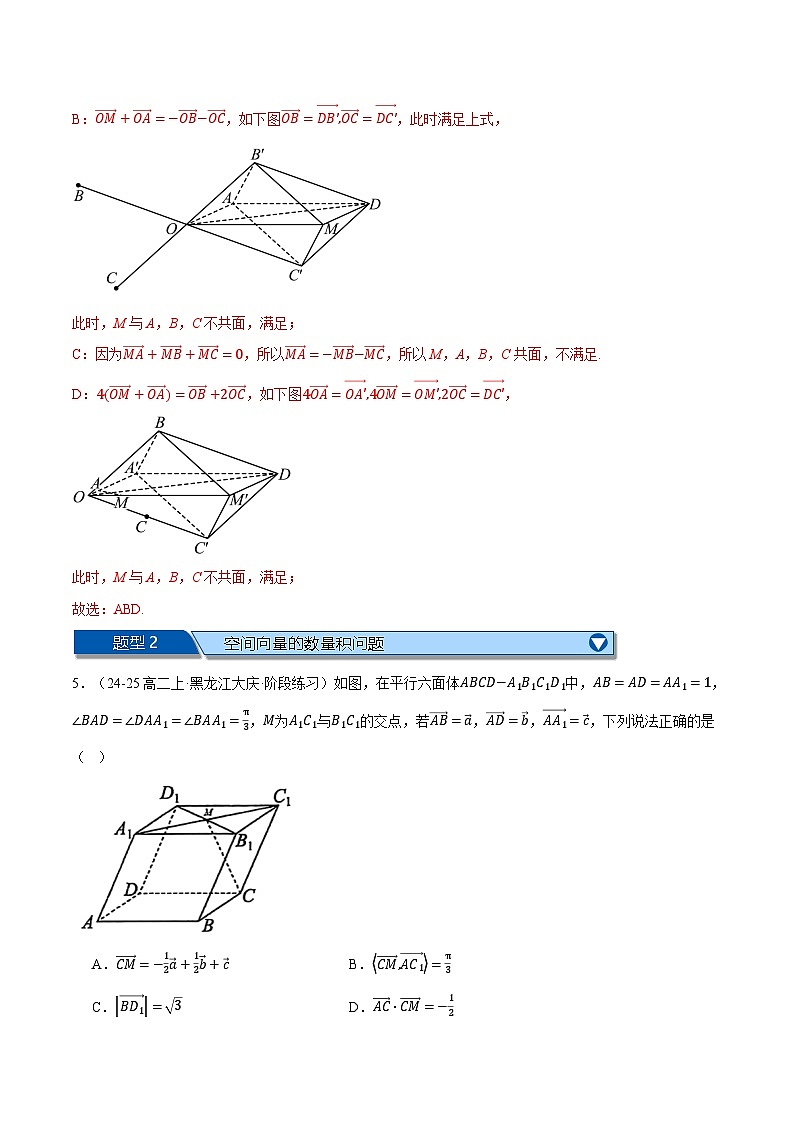
8．（23-24高二上·河北邯郸·期末）如图，平行六面体ABCD−A1B1C1D1的校长均为3，且AB,AD,AA1两两向量的夹角都是60∘，过AC1的平面AEC1F与BB1,DD1分别交于点E,F,DF=2，则（ ）

A．截面BDD1B1的面积为9
B．AE⋅AF=11
C．AC,AA1的夹角是60∘
D．平行六面体ABCD−A1B1C1D1的体积为2722
题型3
空间向量基本定理及其应用
9．（24-25高二上·重庆·期中）如图，空间四边形OABC中，OA=a,OB=b,OC=c，点N在BC上，且CN=13CB，点M为OA中点，则MN等于（ ）
A．12a−23b−13cB．−12a+13b+23c
C．12a−13b−23cD．−12a+23b+13c
10．（24-25高二上·广东深圳·期中）如图，已知空间四边形OABC，其对角线OB,AC,M,N分别是对边OA,BC的中点，点G在线段MN上，且GN=2MG，现用向量OA,OB,OC表示向量OG，设OG=xOA+yOB+zOC，则x+y+z=（ ）
A．23B．1C．13D．12
11．（23-24高二上·陕西宝鸡·期末）如图，在四面体OABC中，OA=a，OB=b，OC=c，点M、 N分别在线段OA、BC上，且2OM=MA，CN=2NB，则MN等于（ ）
A．−13a+23b+13cB．−13a+23b−13c
C．13a−23b+13cD．13a+23b+23c
12．（24-25高二上·吉林·期中）如图，在平行六面体ABCD−A1B1C1D1中，AB=AD=AA1=2，∠BAD=∠A1AB=∠A1AD=60∘,A1C1与B1D1的交点为M，设AB=a,AD=b,AA1=c，则（ ）

A．AM=12a+12b+cB．AM=12a+12b−c
C．AM=11D．cs=51122
题型4
空间向量平行、垂直的坐标表示
13．（24-25高二上·广东深圳·期中）设x,y∈R，向量a=x,2,2,b=2,y,2,c=3,−6,3，且a⊥c,b ∥ c，则x+y=（ ）
A．−8B．−2C．2D．8
14．（24-25高二上·山东泰安·期中）设x,y∈R，向量a=x,1,1，b=1,y,1，c=2,−4,2且a⊥c，b∥c，则a+b=（ ）
A．3B．10C．22D．4
15．（24-25高二上·甘肃庆阳·期中）已知向量n=4,1,2，点A−1,2,1，B2,s,t，且AB→//n→，则s+t=（ ）
A．112B．212C．114D．214
16．（24-25高二上·河南·阶段练习）已知空间向量a=1,2,3,2a+b=0,3,7,c=2,m,6，且a//c，则下列说法正确的是（ ）
A．b=6B．m=4
C．2b+c⊥aD．csb,c=−2142
题型5
利用空间向量研究点、线、面的距离问题
17．（24-25高二上·云南普洱·期中）如图，在棱长为4的正方体ABCD−A1B1C1D1中，M，N分别是A1B1，CD的中点，则点D到截面AMC1N的距离为（ ）

A．63B．263C．223D．423
18．（24-25高二下·全国·课后作业）正方体ABCD−A1B1C1D1的棱长为2，E，F，G，H分别是棱AB，AD，B1C1，D1C1的中点，则平面EFD1B1和平面GHDB之间的距离为（ ）
A．13B．23C．12D．16
19．（24-25高二上·河北张家口·阶段练习）已知四棱锥A−EBCD,AE⊥平面BCDE，底面EBCD是∠E为直角，EB//DC的直角梯形，如图所示，且CD=2EB=2AE=4,DE=23，点F为AD的中点，则F到直线BC的距离为（ ）
A．312B．232C．314D．234
20．（24-25高二上·安徽芜湖·期中）如图，在棱长为2的正方体ABCD−A1B1C1D1中，E,F分别为BB1,CC1的中点，G是线段B1C1上的一个动点，则下列说法正确的是（ ）
A．直线AG与平面AEF所成角的余弦值的取值范围为1515,1010
B．点G到平面AEF的距离为255
C．点B1到AF所在直线的距离为2
D．若线段AA1的中点为H，则GH一定平行于平面AEF
题型6
利用空间向量求空间角
21．（23-24高一下·河北承德·期末）在正四棱锥P−ABCD中，PA=4,AB=2,E是棱PD的中点，则异面直线AE与PC所成角的余弦值是（ ）
A．612B．68C．38D．5624
22．（23-24高三上·福建福州·期中）正四棱柱ABCD−A1B1C1D1中，AB=BC=2，四面体ACB1D1体积为83，则AC1与平面BC1A1所成角的正弦值为（ ）
A．12B．14C．13D．16
23．（23-24高二上·四川凉山·期中）已知圆锥的顶点是P，底面圆心是O，AB为底面直径，∠APB=120∘，PA=4，点C在底面圆周上，且二面角P−AC−O为45∘，下面说法正确的是（ ）
A．AC与平面PAB所成角的正弦值为33
B．O到平面PAC的距离为22
C．PC与AB所成角的余弦值为32
D．平面PAB与平面PAC所成角的正弦值为29
24．（24-25高二上·云南昆明·阶段练习）如图，在正方体ABCD−A1B1C1D1中，点P在线段B1C上运动，则下列结论正确的是（ ）
A．三棱锥P−A1C1D的体积为定值
B．异面直线AP与A1D所成角的取值范围是[π4,π2]
C．平面ADP与平面ABCD所成夹角的余弦值取值范围是[22,1]
D．直线C1P与平面A1C1D所成角的正弦值的最大值为63
题型7
立体几何中的探索性问题
25．（2024·北京怀柔·模拟预测）如图，已知正方体ABCD−A1B1C1D1中，F为线段BC1的中点，E为线段A1C1上的动点，则下列四个结论正确的是（ ）

A．存在点E，使EF//平面ABCD
B．三棱锥B1−ACE的体积随动点E变化而变化
C．直线EF与AD1所成的角不可能等于30°
D．存在点E，使EF⊥平面AB1C1D
26．（23-24高三上·四川成都·期末）如图所示的几何体是由正方形ABCD沿直线AB旋转90°得到的，设G是圆弧CE的中点，H是圆弧DF上的动点（含端点），则下列结论不正确的是（ ）
A．存在点H，使得EH⊥BG
B．存在点H，使得EH//BD
C．存在点H，使得EH//平面BDG
D．存在点H，使得直线EH与平面BDG的所成角为30°
27．（23-24高二下·上海杨浦·期末）如图，已知正方体ABCD−A1B1C1D1的棱长为1，点M为棱AB的中点，点P在正方形BCC1B1内部（不含边界）运动，给出以下三个结论：
①存在点P满足PD1⊥MB1；
②存在点P满足PD1与平面A1D1M所成角的大小为60°；
③存在点P满足MD1+MP=125；
其中正确的个数是（ ）
A．0B．1C．2D．3
28．（24-25高二上·辽宁大连·期中）如图，在多面体ABCDES中，SA⊥平面ABCD，四边形ABCD是正方形，且DE//SA，SA=AB=2DE=2，M，N分别是线段BC,SB的中点，Q是线段DC上的一个动点（含端点D，C），则下列说法正确的是（ ）
A．存在点Q，使得NQ⊥SB
B．存在点Q，使得异面直线NQ与SA所成的角的余弦值为55
C．当点Q自D向C处运动时，直线DC与平面QMN所成的角不变
D．三棱锥Q−AMN体积的最大值是23
题型8
直线与线段的相交关系求斜率范围
平面向量线性运算的坐标表示
平面向量线性运算的坐标表示
29．（24-25高二上·天津滨海新·阶段练习）已知点A(2,3),B(−3,2)， 若直线ax+y+1=0与线段AB 相交，则a的取值范围是（ ）
A．[−1,2]B．(−∞,−1)∪[2,+∞)
C．[−2,1)D．−∞−2∪1+∞
30．（24-25高二上·广东广州·期中）已知点M3,0关于直线x−y−1=0的对称点为P，经过点P作直线l，若直线l与连接A−7,1，B5,8两点的线段总有公共点，则直线l的斜率k的取值范围为（ ）
A．18,32B．−∞,18∪32,+∞
C．−18,32D．−∞,−18∪32,+∞
31．（24-25高二上·陕西西安·阶段练习）过点P0,−1作直线l，若直线l与连接A−2,1，B23,1两点的线段总有公共点，则直线l的倾斜角范围为（ ）
A．π6,π4B．π6,3π4
C．0,π6∪3π4,πD．π6,π2∪3π4,π
32．（23-24高二上·陕西安康·期末）已知直线l过点P−1,2且与线段AB的延长线有公共点，若A−2,−3，B3,0，则直线l的斜率的取值可以是（ ）
A．−14B．0C．14D．45
题型9
根据两直线平行、垂直求参数
平面向量线性运算的坐标表示
平面向量线性运算的坐标表示
33．（24-25高二上·河北保定·期中）若直线l1:ax−3y+2=0与直线l2:3ax+y+3=0垂直，且直线l3:a²x−y+4=0与直线l₄：l:x+a+2y=0垂直，则a=（ ）
A．1B．−1C．2D．−2
34．（24-25高二上·江苏无锡·阶段练习）已知a，b都是正实数，且直线2x−b−3y+6=0与直线bx+ay−5=0互相垂直，则2a+3b的最小值为（ ）
A．12B．10C．8D．25
35．（23-24高二上·陕西西安·期末）已知直线l1:ax−2y−2=0与直线l2:x−a+1y+2=0平行，则实数a的所有取值之和为（ ）
A．-2B．−1C．1D．2
36．（23-24高二上·四川成都·期中）已知直线l1:(a+2)x+3y+4=0，l2:x+ay−4=0，则（ ）
A．当a=0时，直线l1的一个方向向量为(2,3)
B．若l1与l2相互平行，则a=−3或1
C．若l1⊥l2，则a=−12
D．若l1不经过第二象限，则a≤−2
题型10
与距离有关的最值问题
37．（24-25高二上·广东汕头·期中）点A2,−4到直线l:mx−y−4m−8=0（m为任意实数）的距离的最大值是（ ）
A．5B．25C．4D．5
38．（23-24高二上·黑龙江·期中）著名数学家华罗庚曾说过：“数形结合百般好，隔裂分家万事休．”事实上，有很多代数问题可以转化为几何问题加以解决，如：x−a2+y−b2可以转化为平面上点Mx,y与点Na,b的距离．结合上述观点，可得y=x2−2x+5+x2−6x+25的最小值为（ ）
A．210B．22C．2+10D．3+5
39．（24-25高二上·云南昆明·阶段练习）已知点A−1,3，直线l:m+2x−m+1y+2m−1=0，则A到l的距离的最大值为（ ）
A．23B．25C．26D．27
40．（23-24高二下·辽宁·开学考试）对于直线l1:ax+2y+3a=0,l2:3x+(a−1)y+3−a=0，则（ ）
A．l1//l2的充要条件是a=3或a=−2B．当a=25时，l1⊥l2
C．直线l2经过第二象限内的某定点D．点P(1,3)到直线l1的距离的最大值为32
题型11
点、线间的对称问题
41．（2024高三·全国·专题练习）光线自点2,4射入，经倾斜角为135∘的直线l：y=kx＋1反射后经过点5,0，则反射光线还经过点（ ）
A．14,2B．14,1C．13,2D．13,1
42．（24-25高二上·江苏南京·阶段练习）如图所示，已知点A(2,0),B(0,2)，从点P(1,0)射出的光线经直线AB反射后再射到直线OB上，最后经直线OB反射后又回到点P，则光线所经过的路程是（ ）
A．3B．10C．33D．25
43．（24-25高二上·全国·单元测试）唐代诗人李颀的诗《古从军行》开头两句为“白日登山望烽火，黄昏饮马傍交河”，其中隐含了一个有趣的数学问题——“将军饮马”，即将军在白天观望烽火台之后黄昏时从山脚下某处出发，先到河边饮马再回到军营，怎样走才能使总路程最短？在平面直角坐标系中，已知军营所在的位置为B−2,0，若将军从山脚下的点A13,0处出发，河岸线所在直线方程为x+2y=3，则“将军饮马”的最短总路程为（ ）
A．1453B．5C．15D．163
44．（23-24高二上·山西太原·期中）已知直线l1:x+y=0,l2:2x−3y−6=0，则下列说法正确的是（ ）
A．直线l1与l2相交于点65,−65
B．直线l1、l2和x轴围成的三角形的面积为65
C．直线l2关于原点O对称的直线方程为2x−3y+6=0
D．直线l2关于直线l1对称的直线方程为3x−2y+6=0
题型12
圆的切线长及切线方程问题
45．（24-25高二上·江西·阶段练习）已知圆x−12+y−12=r2经过点P2,2，则圆在点P处的切线方程为（ ）
A．x+y−4=0B．x+y=0
C．x−y=0D．x−y−4=0
46．（23-24高二下·浙江温州·期末）已知圆C：x2+y2=4，点P为直线x+y−4=0上一动点，过点P向圆C引两条切线PA，PB，A，B为切点，则线段AB长度的最小值为（ ）
A．22B．32C．4D．42
47．（23-24高二上·安徽黄山·期中）已知直线l:x+ay−1=0(a∈R)是圆C:x2+y2−4x−2y+1=0的对称轴.过点A(−4,a)作圆C的两条切线，切点分别为B、D，则直线BD的方程为（ ）
A．3x+y−5=0B．2x+y−5=0C．3x−y+5=0D．2x+y−5=0
48．（23-24高二上·广西南宁·期中）设圆C:x−12+y−12=3，直线l:x+y+1=0，P为l上的动点，过点P作圆C的两条切线PA、PB，切点分别为A、B，则下列说法中正确的有（ ）
A．PA的取值范围为62,+∞
B．四边形PACB面积的最小值为322
C．存在点P使∠APB=120°
D．直线AB过定点0,0
题型13
直线与圆有关的最值（范围）问题
49．（24-25高二上·重庆·期中）圆C:x−22+y2=4，P是直线l:x+2y−8=0上的动点，过点P作圆C的切线，切点为M，N，那么PC⋅MN的最小值是（ ）
A．55B．1655C．4305D．4
50．（24-25高二上·黑龙江·阶段练习）已知点O是坐标原点，点Q是圆(x−3)2+(y+4)2=1上的动点，点P(t,−t−4)，则当实数t变化时，PQ+PO的最小值为（ ）
A．8B．7C．6D．5
51．（24-25高三上·湖南衡阳·开学考试）已知圆C1:(x−2)2+(y−2)2=14与圆C2:(x+1)2+(y+2)2=14，过动点Mm,n分别作圆C1､圆C2的切线MA,MB（A,B分别为切点），若MA=MB，则M到圆(x+12)2+(y+5)2=4距离的最小值是（ ）
A．192B．154C．192−2D．154−2
52．（24-25高二上·浙江杭州·期中）已知直线l:kx−y+k=0，圆C:x2+y2−6x+5=0，点Px0,y0为圆C上一动点，则下列说法正确的是（ ）
A．x02+y02的最大值为5
B．y0x0的最大值为255
C．x0+y0的最大值为3+22
D．圆心C到直线l的距离最大为4
题型14
直线与圆有关的面积问题
53．（2024·河南洛阳·模拟预测）从直线l:3x+4y=15上的动点P作圆x2+y2=1的两条切线，切点分别为C、D，则∠CPD最大时，四边形OCPD（O为坐标原点）面积是（ ）
A．3B．22C．23D．2
54．（2024·甘肃酒泉·三模）若直线3x−y−3=0分别与x轴，y轴交于A，B两点，动点P在圆x2+(y−1)2=1上，则△ABP面积的取值范围是（ ）
A．[2,32]B．[3,23]C．[3,33]D．[22,32]
55．（24-25高二上·新疆乌鲁木齐·期中）已知点M是直线l：x−y+4=0上的动点，过点M作圆O：x2+y2=4的两条切线，切点为C，D，则四边形OCMD面积的最小值是（ ）
A．2B．2C．22D．4
56．（23-24高三上·广东汕头·期中）已知圆C:(x−2)2+y2=1，点P是直线l:x+y=0上一动点，过点P作直线PA､PB分别与圆C相切于点A､B，则（ ）
A．圆C上恰有一个点到l的距离为12B．直线AB恒过定点32,−12
C．AB的最小值是2D．四边形ACBP面积的最小值为2
题型15
求圆锥曲线的离心率或其取值范围
57．（24-25高二上·江苏盐城·期中）已知点F1、F2是椭圆B:x2a2+y2b2=1a>b>0的左、右焦点，点M为椭圆B上一点，点F1关于∠F1MF2的角平分线的对称点N也在椭圆B上，若cs∠F1MF2=79，则椭圆B的离心率为（ ）
A．36B．33C．1025D．105
58．（24-25高二上·吉林延边·阶段练习）已知椭圆C:x2a2+y2b2=1a>b>0的右焦点为F，Mx1,y1，N−x1,−y1在椭圆C上但不在坐标轴上，若FM=2FA，FN=2FB，且OA⊥OB，则椭圆C的离心率的取值范围为（ ）
A．22,1B．0,22
C．63,1D．0,63
59．（24-25高二上·云南昆明·期中）已知双曲线C:x2a2−y2b2=1(a>0,b>0)的左右焦点分别为F1，F2，点A在C上，点B在y轴上，F1A⊥F1B，F2A=−23F2B，则C的离心率为（ ）
A．52B．6C．355D．62
60．（24-25高二上·江西新余·阶段练习）已知椭圆C:x2a2+y2b2=1(a>b>0)的左、右焦点分别为F1,F2且F1F2=2，点P1,1在椭圆内部，点Q在椭圆上，则椭圆C的离心率可以是（ ）
A．0.3B．0.6C．0.9D．1
题型16
椭圆的弦长与“中点弦”问题
61．（23-24高二下·陕西渭南·期末）已知直线l:mx−y+1=0与椭圆C:x24+y2=1交于A，B两点，当AB取最大值时m的值为（ ）
A．±52B．±32C．±22D．±12
62．（23-24高二上·浙江温州·期中）直线l：y=−2x+1在椭圆y22+x2=1上截得的弦长是（ ）
A．103B．253C．859D．523
63．（24-25高二上·湖北·期中）已知椭圆y29+x24=1与直线l交于A,B两点，若点P(−1,1)为线段AB的中点，则直线l的方程是（ ）
A．9x+4y−13=0B．9x−4y+13=0
C．4x−9y+13=0D．4x−9y+3=0
64．（24-25高二·上海·随堂练习）设椭圆的方程为x22+y24=1，斜率为k≠0的直线不经过原点O，而且与椭圆相交于A、B两点，M为线段AB的中点．下列结论中正确的是（ ）
A．直线AB与OM垂直
B．若点M坐标为1,1，则直线方程为2x+y−3=0
C．若直线方程为y=x+1，则点M坐标为13,34
D．若直线方程为y=x+2，则|AB|=432
题型17
双曲线的弦长与“中点弦”问题
65．（23-24高二上·天津和平·期末）直线l与双曲线x2−y29=1交于A，B两点，线段AB的中点为点M−1,−4，则直线l的斜率为（ ）
A．−49B．49C．−94D．94
66．（2024·山东·模拟预测）过双曲线x2−y2=2的左焦点作直线l，与双曲线交于A,B两点，若AB=4，则这样的直线l有（ ）
A．1条B．2条C．3条D．4条
67．（23-24高二下·重庆沙坪坝·阶段练习）已知双曲线C：x2a2−y2b2=1(a>0,b>0)的一条渐近线方程是y=2x，过其左焦点F(−3,0)作斜率为2的直线l交双曲线C于A，B两点，则截得的弦长|AB|=（ ）
A．7B．8C．9D．10
68．（23-24高二上·广东佛山·期末）设A,B是双曲线y24−x2=1上的两点，下列四个点中，可以作为线段AB中点的是（ ）
A．−1,2B．1,1C．1,3D．2,5
题型18
抛物线的弦长与焦点弦问题
69．（23-24高三上·广东广州·期中）直线l经过抛物线y2=4x的焦点F，且与抛物线交于A，B两点.若AF=3BF，则AB=（ ）
A．83B．3C．163D．32
70．（2024·四川·模拟预测）已知过抛物线C：y2=4x的焦点F的直线l与抛物线C交于A，B两点，若AF=3BF，则AB=（ ）
A．433B．833C．83D．163
71．（2024·山东聊城·三模）已知抛物线C:x2=2py(p>0)的焦点F到其准线的距离为2，过F的直线l与C交于A，B两点，则AB的最小值为（ ）
A．2B．4C．6D．8
72．（24-25高三上·云南昆明·阶段练习）已知拋物线C:x2=2py(p>0)上的动点M到焦点F的距离最小值是2，经过点P2,−3的直线l与C有且仅有一个公共点，直线PF与C交于两点A,B，则（ ）
A．p=2B．抛物线C的准线方程为y=−2
C．AB=58D．满足条件的直线l有2条
题型19
圆锥曲线中的切线与切点弦问题
73．（2024·全国·模拟预测）已知抛物线C:x2=4y，过点P(m,−1)作抛物线的两条切线，两个切点分别为A,B，若|AB|=8，则m的值为（ ）
A．2或−1B．1或−2
C．2或−2D．1或−1
74．（23-24高三下·河南·阶段练习）已知椭圆C:x2+y2t2=1，离心率为22，过P1,2的直线分别与C相切于A，B两点，则直线AB方程为（ ）
A．x+y−1=0或x+4y−1=0B．x+4y−1=0
C．x+y−1=0D．x+y+1=0或x+4y−1=0
75．（23-24高三·江西上饶·阶段练习）已知抛物线y2=2px(p>0))的焦点为F，过F且倾斜角为π4的直线l与抛物线相交于A，B两点，AB=12，过A，B两点分别作抛物线的切线，交于点Q．则下列四个命题中正确的是( )
①QA⊥QB；
②若M(1，1)，P是抛物线上一动点，则|PM|+|PF|的最小值为52；
③1AF+1BF=2；
④△AOB(O为坐标原点)的面积为32.
A．①③B．②④C．①②D．③④
76．（23-24高三下·广东·阶段练习）已知抛物线C：x2=2pyp>0的焦点为F，点P−1,t在C的准线上，过点P作C的两条切线，切点分别为M，N，则（ ）
A．M，F，N三点共线
B．若PF=13PM+23PN，则C的方程为x2=22y
C．当t=−1时，直线MN的方程为y=−12x+1
D．△PMN面积的最小值为332
题型20
圆锥曲线中的面积问题
77．（23-24高二上·福建莆田·期末）已知P为椭圆x24+y2=1y≠−1上任一点，过P作圆C:x2+(y+2)2=1的两条切线PM,PN，切点分别为M,N，则四边形PMCN面积的最大值为（ ）
A．3B．22C．533D．6
78．（23-24高二上·浙江嘉兴·阶段练习）已知双曲线x2a2−y2b2=1(a>0,b>0)的离心率为2，F1,F2分别是双曲线的左､右焦点，点M−a,0,N0,b，点P为线段MN上的动点，当PF1⋅PF2取得最小值和最大值时，△PF1F2的面积分别为S1,S2，则S2S1=（ ）
A．4B．8C．23D．43
79．（23-24高二上·湖北武汉·期中）已知中心在原点O，焦点在y轴上，且离心率为23的椭圆与经过点C−2,0的直线l交于A,B两点，若点C在椭圆内，△OAB的面积被x轴分成两部分，且△OAC与△OBC的面积之比为3:1，则△OAB面积的最大值为（ ）
A．873B．473C．2477D．1277
80．（23-24高三上·江苏连云港·期中）在平面直角坐标系xOy中，已知F为抛物线y2=x的焦点，点Ax1,y1,Bx2,y2在该抛物线上且位于x轴的两侧，OA⋅OB=2，则（ ）
A．x1x2=6B．直线AB过点(2,0)
C．△ABO的面积最小值是22D．△ABO与△AFO面积之和的最小值是3
题型21
圆锥曲线中的参数范围及最值问题
81．（23-24高二下·福建泉州·期末）已知抛物线Γ：y=14x2的焦点为F，过F的直线l交Γ于点A,B，分别在点A,B处作Γ的两条切线，两条切线交于点P，则1PA2+1PB2的取值范围是（ ）
A．0,1B．0,12C．0,14D．14,12
82．（24-25高二上·全国·课后作业）已知A,B是椭圆x2a2+y2b2=1(a>b>0)长轴的两个端点，M,N是椭圆上关于x轴对称的两点，直线AM,BN的斜率分别为k1,k2k1k2≠0).若椭圆的离心率为32，则k1+k2的最小值为（ ）
A．1B．2C．32D．3
83．（2024·江西赣州·一模）已知M、N是双曲线C:x2a2−y2b2=1a>0,b>0上关于原点对称的两点，P是C上异于M、N的动点，设直线PM、PN的斜率分别为k1、k2．若直线y=12x与曲线C没有公共点，当双曲线C的离心率取得最大值时，且2≤k1≤3，则k2的取值范围是（ ）
A．112,18B．−18,−112C．13,12D．−12,−13
84．（23-24高三上·广东广州·阶段练习）已知F为椭圆C:x216+y28=1的左焦点，经过原点O的直线l与椭圆C交于A,B两点，AD⊥x轴，垂足为D，BD与椭圆C的另一个交点为E（异于点A），则（ ）
A．AB⊥AEB．△ABD面积的最大值为42
C．△ABF周长的最小值为12D．1AF+16BF的最小值为258
题型22
圆锥曲线中的向量问题
85．（2024·黑龙江哈尔滨·二模）已知抛物线y=116x2与双曲线y2a2−x2=1a>0有共同的焦点F，O为坐标原点，P在x轴上方且在双曲线上，则OP⋅FP的最小值为（ ）
A．415−16B．16−415C．15−415D．415−15
86．（23-24高二上·北京·期中）已知椭圆M:x24+y2=1的上、下顶点为A,B，过点P0,2的直线l与椭圆M相交于两个不同的点C,D（C在线段PD之间），则OC⋅OD的取值范围为（ ）
A．−1,16B．−1,16C．−1,134D．−1,134
87．（2024·湖北黄石·三模）已知Mx0,y0为双曲线x2−y2=4上的动点，x0>0，y0≥0，直线l1：x0x−y0y=4与双曲线的两条渐近线交于P，Q两点（点P在第一象限），R与Q在同一条渐近线上，则RP⋅RQ的最小值为（ ）
A．−8B．−4C．0D．−2
88．（2024·湖北·模拟预测）已知椭圆C:x2a2+y2b2=1a>b>0的离心率为12，左，右焦点分别为F1，F2，过F2且倾斜角为π3的直线与椭圆C交于A，B两点（点A在第一象限），P是椭圆C上任意一点，则（ ）
A．a，b满足b=32aB．PF1⋅PF2的最大值为b2
C．存在点P，使得∠F1PF2=512πD．3BF2=5F2A
题型23
圆锥曲线中的定点、定值、定直线问题
89．（23-24高二上·江苏南通·阶段练习）已知椭圆x24+y22=1上的两个动点P，Q，设Px1,y1，Qx2,y2，且x1+x2=2.线段PQ的垂直平分线经过一个定点，则定点坐标为（ ）
A．12,0B．1,0C．2,0D．−1,0
90．（23-24高二下·安徽安庆·期末）已知抛物线C：y2=4x内有一点A3,−2，过点A作直线l与该抛物线交于P、Q两点，经过点B3,−6和点Q的直线与该抛物线交于另一点T，则直线PT过定点的坐标为（ ）
A．−1,0B．1,0C．−3,0D．3,0
91．（2024·广西梧州·一模）已知双曲线C:x2a2−y24=1a>0的左、右焦点分别为F1，F2，P为双曲线C右支上的动点，过P作两渐近线的垂线，垂足分别为A，B．若圆x−22+y2=1与双曲线C的渐近线相切，则下列结论正确的有（ ）个
①a=4；
②PA⋅PB为定值；
③双曲线C的离心率e=233；
④当点P异于顶点时，△PF1F2的内切圆的圆心总在直线x=23上．
A．1B．2C．3D．4
92．（2024·浙江绍兴·模拟预测）已知椭圆x24+y2=1的左顶点为A，上、下顶点分别为C,D，动点Px1,y1,Qx2,y2在椭圆上（点P在第一象限，点Q在第四象限），O是坐标原点，若△OPQ的面积为1，则（ ）
A．y1x2为定值B．CP//AQ
C．△OCP与△OAQ的面积相等D．△OCP与△ODQ的面积和为定值