湘教版（2024）第2章 实数2.1 平方根公开课ppt课件

这是一份湘教版（2024）第2章 实数2.1 平方根公开课ppt课件，共27页。PPT课件主要包含了平方根，填一填，a的算术平方根，算术平方根的性质，练一练，不正确是4等内容，欢迎下载使用。
1.了解平方根及算术平方根的概念，会用根号表示 一个数的算术平方根.（重点）2.会求非负数的平方根与算术平方根.（难点）
某家庭在装修儿童房时需铺地垫 10.8 m2，刚好用去正方形的地垫 30 块. 你能算出每块地垫的边长是多少吗？
解：每块正方形地垫的面积是 10.8÷30 = 0.36 (m2).
即边长×边长 = 0.36.
由于 0.62 = 0.36，
因此面积为 0.36 m2 的正方形地垫的边长是 0.6 m.
请你说一说解决问题的思路．
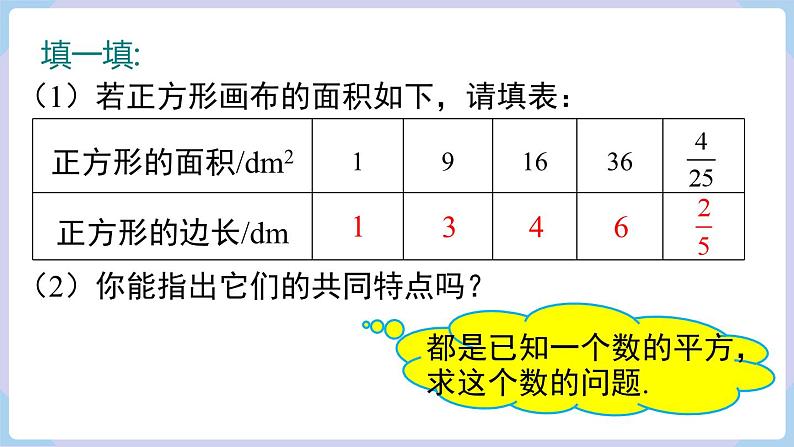
　　学校要举行美术作品比赛，小鸥想裁出一块面积为25 dm2 的正方形画布，画上自己的得意之作参加比赛，这块正方形画布的边长应取多少？
（1）若正方形画布的面积如下，请填表：
（2）你能指出它们的共同特点吗？
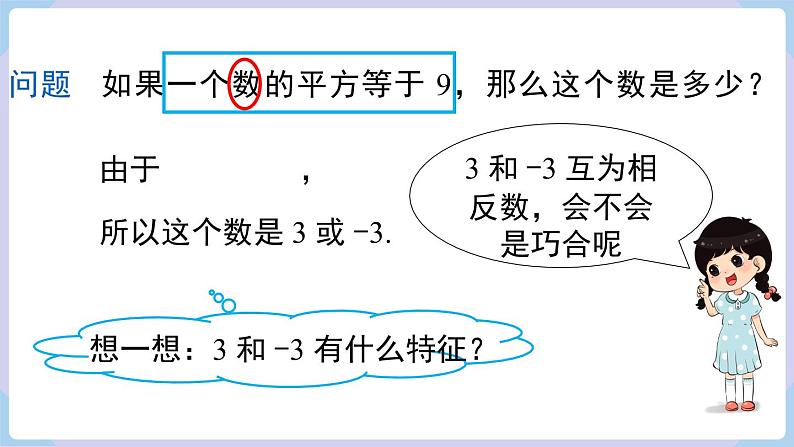
问题 如果一个数的平方等于 9，那么这个数是多少？
3 和 -3 互为相反数，会不会是巧合呢
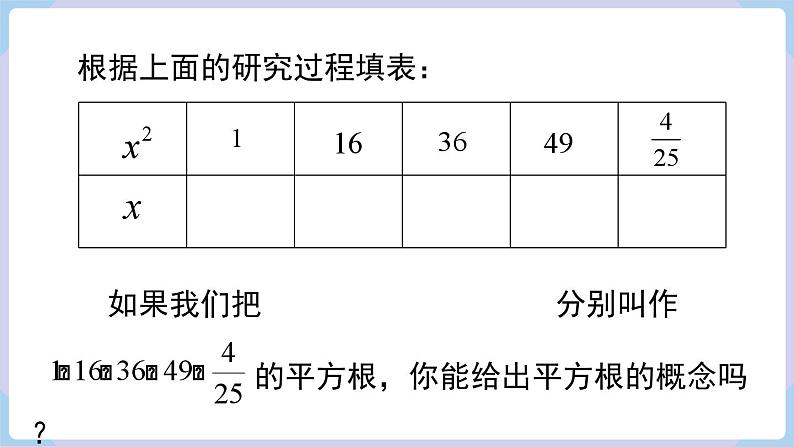
根据上面的研究过程填表：
如果我们把 　 分别叫作 　 的平方根，你能给出平方根的概念吗？
根据上述问题，即要找出一个数，使它的平方等于给定的数. 由此我们抽象出下述概念：
如果有一个数 r，使得 r2 = a，那么 r叫作 a 的一个平方根，也叫作二次方根.
因为边长大于 2 的正方形，它的面积一定大于 4，所以，比 2 大的数都不是 4 的平方根.
类似地，边长小于 2 的正方形，它的面积一定小于 4，因此，比 2 小的正数都不是 4 的平方根.
思考：除了 2 和 －2 以外，4 的平方根还有其他的数吗？
如果 r 是正数 a 的一个平方根，那么 a 的平方根有且只有两个：r 与 -r.
由于 02 = 0，而非零数的平方不等于 0，因此零的平方根就是 0 本身.
由于同号两数相乘得正数，且 02 = 0，即在迄今为止我们所认识的数中，任何一个数的平方都不会是负数，因此负数没有平方根.
小结：正数平方根有两个，它们互为相反数；零的平方根是 0；负数没有平方根.
说一说 零的平方根是多少？负数有平方根吗？
求一个非负数的平方根的运算，叫作开平方.开平方与平方互为逆运算.
+1-1+2-2+3-3
例1 分别求下列各数的平方根：36， ，1.21.
解：由于 62 = 36，
因此 36 的平方根是 6 与 -6.
由于 1.12 = 1.21，
因此 1.21 的平方根是 1.1 与 -1.1.
① 的平方根是_______； ② (－16)2 的平方根是_______.
例2 已知一个正数的两个平方根分别是 2a－2和 a－4，则 a 的值是________．
方法总结：本题考查了平方根的概念．一个正数有两个平方根，它们是互为相反数，两个数互为相反数，它们的和为 0.
解析：因为一个正数的两个平方根分别是 2a－2 和 a－4， 所以2a－2＋a－4＝0，解得 a＝2.
思考：正数、负数、0 的算术平方各有几个？
正数的算术平方根是一个正数，0 的算术平方根还是 0，负数没有算术平方根.
算术平方根的概念及性质
算术平方根具有双重非负性
判断下列说法是否正确. ①25 的算术平方根是 5 （ ）； ②25 的平方根是 5 （ ）； ③5 是 25 的平方根 （ ）.
注意区分“平方根”与“算术平方根”的意义.
例3 分别求下列各数的算术平方根： （1）100； （2） ； （3）0.49.
方法归纳：几个非负式的和为 0，则每个式均为 0，初中阶段学过的非负式有绝对值、偶次幂及一个数的算术平方根.
解：因为 | m - 1| ≥0， ≥0， 又 | m - 1| + = 0， 所以 | m - 1 | = 0， = 0. 所以 m = 1，n = -3. 所以 m + n = 1 + (-3) = -2.
3.若 ，则 a = ；
2.若 ，则 m = ；
4.若|a - 3|+ ，则代数式(a + b)2025 =___.
1.若 |a + 3| = 0 ， 则 a = ；
1. 包含关系：平方根包含算术平方根，算术平方根是平方根的一种.
平方根与算术平方根的联系与区别：
2. 只有非负数才有平方根和算术平方根.
3. 0 的平方根是 0，算术平方根也是 0.
1. 个数不同：一个正数有两个平方根， 但只有一个算术平方根.
1. 分别求 64，6.25 的平方根，并用式子表示.
2. 分别求 81，0.16 的算术平方根.
解：81 的算术平方根是 9， . 0.16 的算术平方根是 0.4，
3. 判断下列说法是否正确.
（4）(-4)2 的平方根是 -4.
4. 已知一个自然数的算术平方根是 a，则按从小到大 排该自然数的后一个自然数的算术平方根是（ ） A. a + 1 B. C. a2 + 1 D.
5.已知 3(x - 1)2 = 363 ，求 x 的值．
解：因为 3(x - 1)2 = 363，
所以 (x - 1)2 = 121，
所以 x = 12 或 x =－10.