黑龙江省齐齐哈尔市克东县2024届九年级上学期期末模拟考试数学试卷(含答案)

这是一份黑龙江省齐齐哈尔市克东县2024届九年级上学期期末模拟考试数学试卷(含答案)，共15页。
模拟试卷
一．选择题（共10小题，满分30分，每小题3分）
1．（3分）下列图形中，既是轴对称又是中心对称图形的是（ ）
A．B．C．D．
2．（3分）如图，在矩形ABCD中，以点D为圆心，AD为半径作弧与BD交于点E，以点B为圆心，AB为半径作弧与BD交于点F．设AB＝a，AD＝b，则（ ）
A．线段DF的长是方程x2+2ax＝b2的一个解
B．线段DF的长是方程x2﹣2ax＝b2的一个解
C．线段BE的长是方程x2+bx＝a2的一个解
D．线段BE的长是方程x2﹣bx＝a2的一个解
3．（3分）下列事件中，是必然事件的是（ ）
A．通常加热到100℃时，水沸腾
B．篮球队员在罚球线上投篮一次，未投中
C．射击运动员射击一次，命中靶心
D．掷一次骰子，向上一面的点数为6
4．（3分）二次函数y＝ax2+bx+c（a≠0）图象上部分点的坐标（x，y）对应值列表如下，则此抛物线的对称轴为（ ）
A．直线x＝﹣3B．直线x＝﹣2C．直线x＝﹣1D．直线x＝0
5．（3分）已知⊙O的半径为1，直线l上有一点P满足PO＝1，则直线l与⊙O的位置关系是（ ）
A．相切B．相离
C．相切或相离D．相切或相交
6．（3分）若A（﹣1，y1），B（1，y2），C（4，y3）三点都在二次函数y＝﹣（x﹣2）2+1的图象上，则y1，y2，y3的大小关系为（ ）
A．y1＜y3＜y2B．y3＜y1＜y2C．y1＜y2＜y3D．y3＜y2＜y1
7．（3分）下列说法不正确的有（ ）
①直径是弦，弦是直径；②长度相等的弧是等弧；③在同圆或等圆中，相等的圆心角所对的弧相等；④在同圆或等圆中，相等的弦所对的圆周角相等．
A．1个B．2个C．3个D．4个
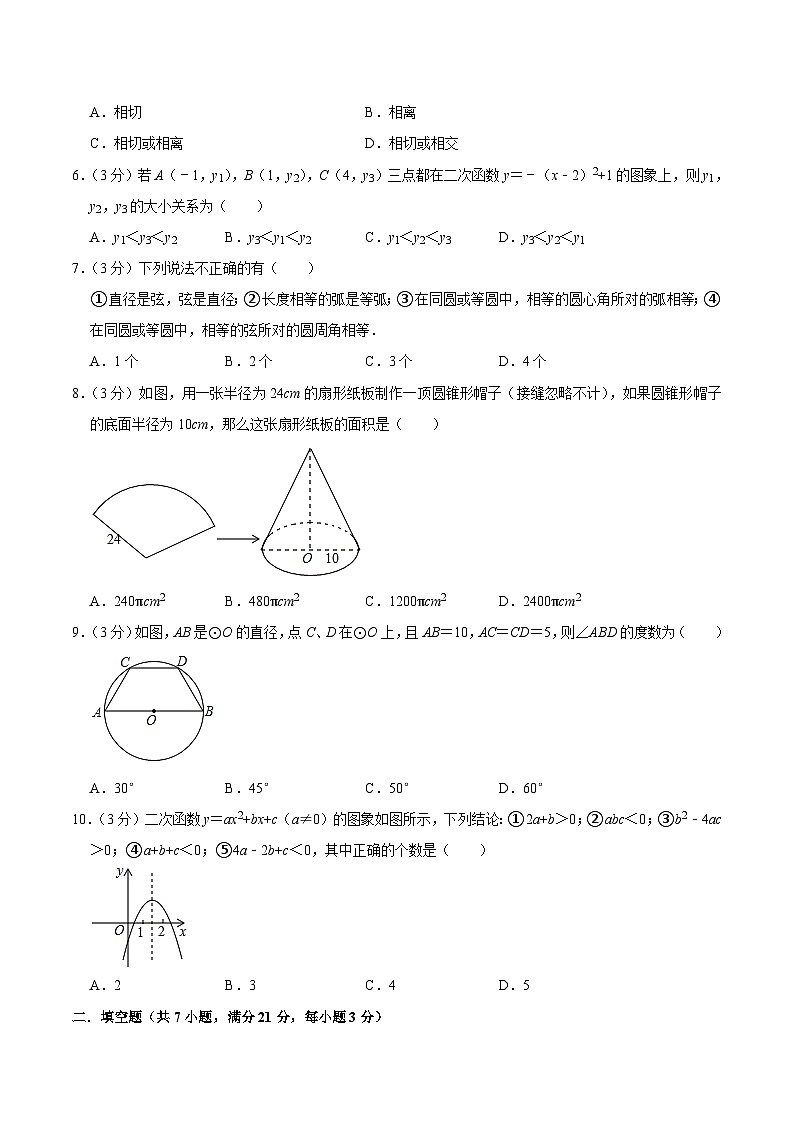
8．（3分）如图，用一张半径为24cm的扇形纸板制作一顶圆锥形帽子（接缝忽略不计），如果圆锥形帽子的底面半径为10cm，那么这张扇形纸板的面积是（ ）
A．240πcm2B．480πcm2C．1200πcm2D．2400πcm2
9．（3分）如图，AB是⊙O的直径，点C、D在⊙O上，且AB＝10，AC＝CD＝5，则∠ABD的度数为（ ）
A．30°B．45°C．50°D．60°
10．（3分）二次函数y＝ax2+bx+c（a≠0）的图象如图所示，下列结论：①2a+b＞0；②abc＜0；③b2﹣4ac＞0；④a+b+c＜0；⑤4a﹣2b+c＜0，其中正确的个数是（ ）
A．2B．3C．4D．5
二．填空题（共7小题，满分21分，每小题3分）
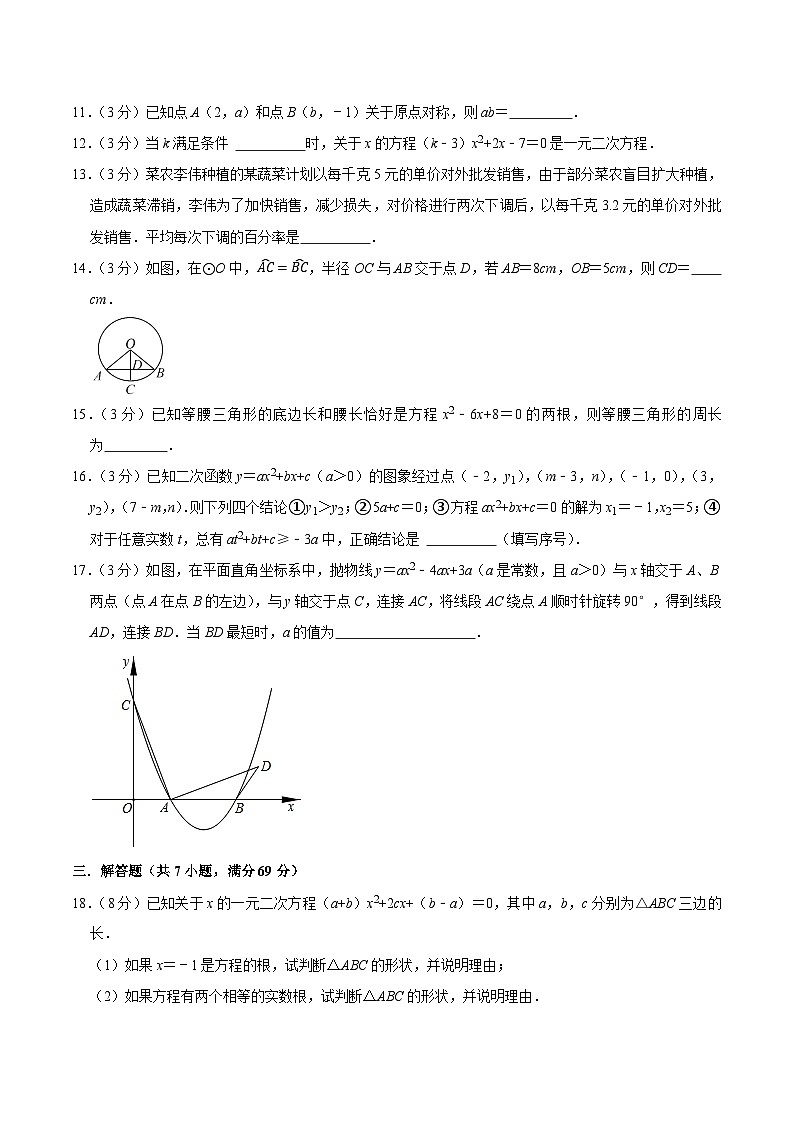
11．（3分）已知点A（2，a）和点B（b，﹣1）关于原点对称，则ab＝ ．
12．（3分）当k满足条件 时，关于x的方程（k﹣3）x2+2x﹣7＝0是一元二次方程．
13．（3分）菜农李伟种植的某蔬菜计划以每千克5元的单价对外批发销售，由于部分菜农盲目扩大种植，造成蔬菜滞销，李伟为了加快销售，减少损失，对价格进行两次下调后，以每千克3.2元的单价对外批发销售．平均每次下调的百分率是 ．
14．（3分）如图，在⊙O中，AC=BC，半径OC与AB交于点D，若AB＝8cm，OB＝5cm，则CD＝ cm．
15．（3分）已知等腰三角形的底边长和腰长恰好是方程x2﹣6x+8＝0的两根，则等腰三角形的周长为 ．
16．（3分）已知二次函数y＝ax2+bx+c（a＞0）的图象经过点（﹣2，y1），（m﹣3，n），（﹣1，0），（3，y2），（7﹣m，n）．则下列四个结论①y1＞y2；②5a+c＝0；③方程ax2+bx+c＝0的解为x1＝﹣1，x2＝5；④对于任意实数t，总有at2+bt+c≥﹣3a中，正确结论是 （填写序号）．
17．（3分）如图，在平面直角坐标系中，抛物线y＝ax2﹣4ax+3a（a是常数，且a＞0）与x轴交于A、B两点（点A在点B的左边），与y轴交于点C，连接AC，将线段AC绕点A顺时针旋转90°，得到线段AD，连接BD．当BD最短时，a的值为 ．
三．解答题（共7小题，满分69分）
18．（8分）已知关于x的一元二次方程（a+b）x2+2cx+（b﹣a）＝0，其中a，b，c分别为△ABC三边的长．
（1）如果x＝﹣1是方程的根，试判断△ABC的形状，并说明理由；
（2）如果方程有两个相等的实数根，试判断△ABC的形状，并说明理由．
19．（10分）一只不透明的袋子中，装有2个白球和1个红球，这些球除颜色外都相同．
（1）小明认为，搅匀后从中任意摸出一个球，不是白球就是红球是等可能的，你同意他的说法吗？为什么？
（2）搅匀后从中一把摸出两个球，请通过列表和树状图求出两个球都是白球的概率．
20．（10分）在如图所示的平面直角坐标系中，△ABC的三个顶点都在小正方形的顶点处，请结合图完成下列各题：
（1）填空：tan∠ABC＝ ；AB＝ （结果保留根号）．
（2）将△ABC绕原点O旋转180°，画出旋转对应的△A′B′C′，并求直线A′C′的函数表达式．
21．（10分）如图，以△ABC的边AB为直径的⊙O交AC于点F，点E是BF的中点，连接BE并延长交AC于点D，若∠CBD=12∠CAB．
（1）求证：BC是⊙O的切线；
（2）若⊙O的半径为2，cs∠BAC=25，求CD的长．
22．（10分）某商品的进价为每件20元，售价为每件30元，每月可卖出180件，该商品每台售价（元）与月销量（台）满足的函数关系式如下表所示．已知该商品计划涨价销售，但每件售价不能高于35元．设每件商品的售价上涨x元（x为整数）时，月销售利润为w元．
（1）上述表格中，y＝ （用含x的代数式表示）；
（2）若销售该商品每月所获利润为1920元，那么每件商品的售价应上涨多少元？
（3）当售价定为多少元时，商场每月销售该商品所获得的利润w最大？最大利润是多少？
23．（10分）如图，△ABC和△BDE都是等腰直角三角形，∠ACB＝∠DBE＝90°，连接CD，以CA、CD为邻边作▱CAFD，连接CE，BF．
（1）如图1，当D在BC边上时，请直接写出CE与BF的关系；
（2）如图2，将图1中的△BDE绕点B顺时针旋转到图2的位置，其他条件不变，（1）中的结论是否成立？若成立，请给予证明；若不成立，请说明理由；
（3）若AC＝3，BD＝2，将图1中的△BDE绕点B顺时针旋转一周，当BD与直线BC夹角为30°时，请直接写出CE的值．
24．（11分）在平面直角坐标系中，抛物线C外：y=-16x2-76x+1，抛物线C内：y＝ax2+bx的对称轴为直线x=-1110，且C内的图象经过点A（﹣3，﹣2），动直线x＝t与抛物线C内交于点M，与抛物线C外交于点N．
（1）求抛物线C内的表达式．
（2）当△AMN是以MN为直角边的等腰直角三角形时，求t的值．
（3）在（2）的条件下，设抛物线C外与y轴交于点B，连接AM交y轴于点P，连接PN．若平面内有一点G，且PG＝1，是否存在这样的点G，使得∠GNP＝∠ONB？若存在，直接写出点G的坐标，若不存在，说明理由．
2023-2024学年黑龙江省齐齐哈尔市克东县九年级（上）期末数学模拟试卷
参考答案与试题解析
一．选择题（共10小题，满分30分，每小题3分）
1．B．
2．A．
3．A．
4．C．
5．D．
6．A．
7．C．
8．A．
9．D．
10．B．
二．填空题（共7小题，满分21分，每小题3分）
11．﹣2．
12．k≠3．
13．20%．
14．2．
15．10．
16．①②③．
17．23．
三．解答题（共7小题，满分69分）
18．解：（1）△ABC是等腰三角形，理由如下：
∵x＝﹣1一元二次方程（a+b）x2+2cx+（b﹣a）＝0的根，
∴（a+b）﹣2c+（b﹣a）＝0，
a+b﹣2c+b﹣a＝0，
b﹣c＝0，
∴b＝c，
∴△ABC是等腰三角形．
（2）△ABC是直角三角形，理由如下：
∵方程有两个相等的实数根，
∴（2c）2﹣4（a+b）（b﹣a）＝0，
∴a2+c2＝b2，
∴△ABC是直角三角形．
19．解：（1）不同意小明的说法，因为摸出白球的概率是23，摸出红球的概率是13，因此摸出白球和摸出红球不是等可能的；
（2）用树状图表示所有可能出现的结果如下：
∴一共有6种情况，两个球都是白球的有2种情况，
∴P（两个球都是白球）=26=13；
答：从中摸出两个球，两个球都是白球的概率为13．
20．解：（1）tan∠ABC=32；AB=22+32=13；
故答案为32，13；
（2）如图，A′（1，﹣4），B′（3，﹣1），C′（2，﹣1），△A′B′C′为所作；
设直线A′C′的函数表达式为y＝kx+b，
把A′（1，﹣4），C′（2，﹣1）代入得k+b=-42k+b=-1，解得k=3b=-7，
所以直线A′C′的函数表达式为y＝3x﹣7．
21．（1）证明：连接AE，
∵点E是BF的中点，
∴EF=BE，
∴∠BAE＝∠EAF，
∵AB是直径，
∴∠AEB＝90°，
∴∠BAE+∠ABE＝90°，
∵∠CBD=12∠CAB，
∴∠CBD+∠ABE＝90°＝∠ABC，
∴AB⊥BD，
又∵AB是直径，
∴BC是⊙O的切线；
（2）∵cs∠BAC=25=ABAC，AB＝2OB＝4，
∴AC＝10，
∵∠AEB＝∠AED＝90°，∠BAE＝∠EAF，
∴∠ABE＝∠ADE，
∴AB＝AD＝4，
∴CD＝6．
22．解：（1）由表格数据可得，y与的函数解析式为：y＝180﹣10x，
故答案为：y＝180﹣10x；
（2）由题意得：1920＝（30﹣20+x）（180﹣10x），
即x2﹣8x+12＝0（0≤x≤5，且x为整数），
解得：x＝2或x＝6，
∵0≤x≤5，
∴x＝2，
∴当x＝2时，y的值为1920；
（3）由题意得：w＝（30﹣20+x）（180﹣10x）＝﹣10x2+80x+1800（0≤x≤5，且x为整数）；
∵﹣10＜0，
∴当x=-802×(-10)=4时，w最大＝1960元；
∴每件商品的售价为34元．
答：每件商品的售价为34元时，商品的利润最大，为1960元．
23．解：（1）CE＝BF，CE⊥BF．
如图1，设CE与BF相交于点M，
∵△ABC和△BDE均为等腰直角三角形，∠ACB＝∠DBE＝90°，
∴AC＝BC，BE＝DB，
∵四边形CAFD是平行四边形，
∴CA＝DF＝BC，CA∥DF，∠ACB＝∠FDB，
∴∠CBE＝∠FDB＝90°，
∴△BEC≌△DBF（SAS）．
∴CE＝BF，∠BCE＝∠DFB，
∵∠DFB+∠DBF＝90°，
∴∠BCE+∠DBF＝90°，
∴∠CMB＝90°，
∴CE⊥BF，
（2）成立．
证明：延长FD交BC于点G，
∵四边形ACDF是平行四边形，
∴AC∥FD，AC＝FD，
∴∠DGB＝∠ACB＝90°，
∴∠FDB＝∠DGB+∠DBG，
∴∠FDB＝90°+∠DBG，
∵∠DBE＝90°，
∴∠CBE＝90°+∠DBG，
∴∠FDB＝∠CBE，
∵△ABC是等腰直角三角形，
∴AC＝BC，
又∵AC＝DF，
∴BC＝DF，
∵BD＝BE，
∴△CBE≌△FDB（SAS），
∴CE＝BF，∠ECB＝∠BFG，
∵∠BFG+∠FBG＝90°，
∴∠ECB+∠FBG＝90°，
∴CE⊥BF；
（3）如图2，由（2）知∠DGB＝90°，BF＝CE，
∵∠DBC＝30°，BD＝2，
∴DG＝1，BG=3，
∵AC＝3，AC＝DF，
∴FG＝DF+DG＝3+1＝4，
∴BF=FG2+BG2=42+(3)2=19，
∴CE=19；
如图3，延长CB交DF于点M，
∵AC∥DF，AC⊥BC，
∴BM⊥DF，
∴∠BMF＝∠BMD＝90°，
∵∠MBD＝30°，BD＝2，
∴DM＝1，BM=3，
∵AC＝DF＝3，
∴FM＝DF﹣DM＝3﹣1＝2，
∴BF=BM2+FM2=3+4=7，
∴CE=7．
∴CE的长为19或7．
24．解：（1）∵y＝ax2+bx的对称轴为直线x=-1110，且C内的图象经过点A（﹣3，﹣2），
∴-b2a=-11109a-3b=-2，
解得：a=-56b=-116，
∴抛物线C内的表达式为y=-56x2-116x；
（2）∵动直线x＝t与抛物线C内交于点M，与抛物线C外交于点N．
∴M（t，-56t2-116t），N（t，-16t2-76t+1），
∵△AMN是以MN为直角边的等腰直角三角形，A（﹣3，﹣2），
∴∠ANM＝90°或∠AMN＝90°，
当∠ANM＝90°时，-16t2-76t+1＝﹣2，
解得：t1＝﹣9，t2＝2，
当t＝﹣9时，AN＝﹣3﹣（﹣9）＝6，MN＝﹣2﹣[-56×（﹣9）2-116×（﹣9）]＝49，
∵AN≠MN，
∴t＝﹣9不符合题意，舍去；
当t＝2时，AN＝2﹣（﹣3）＝5，MN＝﹣2﹣（-56×22-116×2）＝5
∵AN＝MN，
∴△AMN是以MN为直角边的等腰直角三角形；
当∠AMN＝90°时，-56t2-116t＝﹣2，
解得：t1＝﹣3，t2=45，
当t＝﹣3时，AM＝0，不符合题意，舍去，
当t=45时，AM=45-（﹣3）=195，MN=4925，
∵AM≠MN，
∴t=45不符合题意，舍去；
综上所述，△AMN是以MN为直角边的等腰直角三角形时，t＝2．
（3）存在点G使得∠GNP＝∠ONB
如图，连接BN，ON，作∠GNP＝∠ONB，使NG交y轴于G，且G在P上方，设AN交y轴于R，则R（0，﹣2），
由（2）知，t＝2，
∴N（2，﹣2），M（2，﹣7），
设直线AM解析式为y＝kx+c，将A（﹣3，﹣2），M（2，﹣7）代入，
得-3k+c=-22k+c=-7，
∴k=-1c=-5，
∴直线AM解析式为y＝﹣x﹣5，
令x＝0，得y＝﹣5，
∴P（0，﹣5），
在y=-16x2-76x+1中，令x＝0，得y＝1，
∴B（0，1），
在Rt△BNR中，BN=BR2+RN2=32+22=13，
在Rt△PNR中，PN=PR2+RN2=32+22=13，
∴BN＝PN，
∴∠NBO＝∠NPR，
∵∠GNP＝∠ONB，
∴△GNP≌△ONB（ASA），
∴PG＝OB＝1，
∴G（0，﹣4）．
根据①可得G（0，﹣4）符合要求，作点G关于直线PN的对称点G′，
设直线PN解析式为y＝mx+n，
∵P（0，﹣5），N（2，﹣2），
∴n=-52m+n=-2，
解得：m=-32n=-5，
∴直线PN解析式为y=32x﹣5，
∵GG′⊥PN，
∴直线GG′解析式为y=-23x﹣4，
设G′（t，-23t﹣4），
∵点G，G′关于直线PN的对称，
∴PG′＝PG，
∴t2+[-23t﹣4﹣（﹣5）]2＝12，
解得t1＝0（舍去），t2=1213，
当t=1213时，-23t﹣4=-23×1213-4=-6013，
∴G′（1213，-6013），
设直线NG的解析式为y＝k1x+b1，将N（2，﹣2），G（0，﹣4）代入，
得2k1+b1=-2b1=-4，
解得k1=1b1=-4，
∴直线NG的解析式为y＝x﹣4，
设直线NG上存在另一点G1（t，t﹣4），满足PG1＝1，
则（t﹣0）2+（t﹣4+5）2＝12，
解得t＝0（舍去）或t＝﹣1，
∴G1（﹣1，﹣5），
设直线NG′的解析式为y＝k2x+b2，将N（2，﹣2），G′（1213，-6013）代入，
得2k2+b2=-21213k2+b2=-6013，
解得k2=177b2=-487，
∴直线NG′的解析式为y=177x-487，
设直线NG上存在另一点G2（t，177t-487），满足PG2＝1，
则（t﹣0）2+（177t-487+5）2＝12，
解得：t=513或t=1213（舍去），
∴G（513，-7713），
综上所述，点G坐标为（0，﹣4）或（1213，-6013）或（﹣1，﹣5）或（513，-7713）．
x
…
﹣3
﹣2
﹣1
0
■
…
y
…
0
﹣3
■
﹣3
﹣5
…
每台售价（元）
30
31
32
…
30+x
月销售量（台）
180
170
160
…
y