浙江省温州市永嘉县五校联考2025届九年级上学期期中考试数学试卷(含答案)

这是一份浙江省温州市永嘉县五校联考2025届九年级上学期期中考试数学试卷(含答案)，共19页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

一、单选题
1．如图为各个城市的轨道交通标志,将其按顺时针方向旋转后得到的图形不变的是( )
A.B.C.D.
2．二次函数的一次项系数是( )
A.B.1C.3D.5
3．下列函数图像经过原点的是( )
A.B.C.D.
4．如图,点A、B、C在上,已知,则的度数是( )
A.B.C.D.
5．小明从盒子里摸球,每次摸出一个后再放回盒中,他连续摸5次,每次摸到的都是红球,下面说法正确的是( )
A.盒子里一定都是红球B.他第6次摸到的一定还是红球
C.他第6次摸到的可能还是红球D.盒子里一定还有其他颜色的球
6．在平面直角坐标系中,将二次函数向左平移2个单位,所得函数的解析式为( )
A.B.C.D.
7．校园内有一块三角形的花坛,现要在花坛内建一景观喷泉,要使喷泉到花坛三个顶点的距离相等,喷泉的位置应选在这个三角形花坛的( )
A.外心B.垂心C.重心D.内心
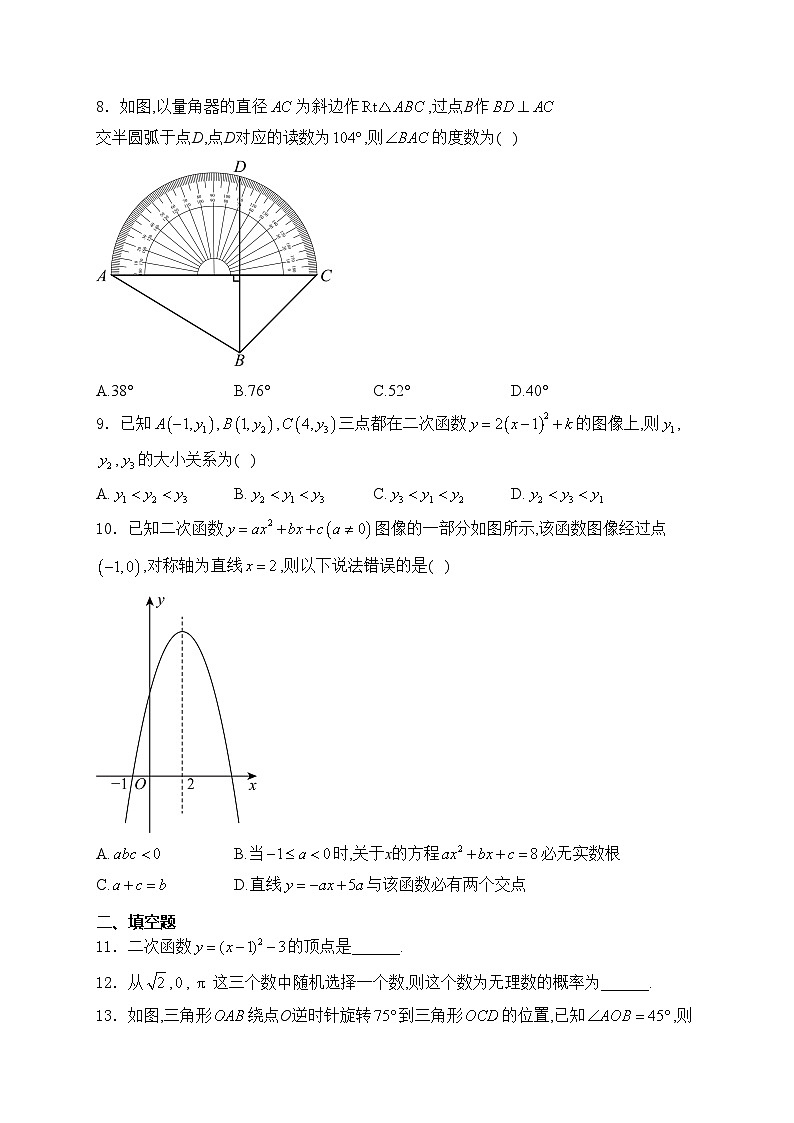
8．如图,以量角器的直径为斜边作,过点B作交半圆弧于点D,点D对应的读数为,则的度数为( )
A.38°B.76°C.52°D.40°
9．已知,,三点都在二次函数的图像上,则,,的大小关系为( )
A.B.C.D.
10．已知二次函数图像的一部分如图所示,该函数图像经过点,对称轴为直线,则以下说法错误的是( )
A.B.当时,关于x的方程必无实数根
C.D.直线与该函数必有两个交点
二、填空题
11．二次函数的顶点是______.
12．从,,这三个数中随机选择一个数,则这个数为无理数的概率为______.
13．如图,三角形绕点O逆时针旋转到三角形的位置,已知,则______.
14．同一平面内,内一点P到圆上的最大距离为,最小距离为,则的半径为______.
15．如图所示,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果园”.已知点A、B、C、D分别是“果园”与坐标轴的交点,抛物线的对称轴为直线,且,为半圆的直径,则这个“果园”被y轴截得的弦的长为______.
16．如图以为直径的半圆上,,点C是半圆弧上的任意点,F为弧上的中点,连结交于点E,作于点D,连结,若为的角平分线,则______,______.
三、解答题
17．已知函数.
(1)若点在此函数图象上,求该二次函数表达式及函数图象的开口方向；
(2)在(1)的条件下,判断点是否在此函数图象上.
18．近期教育局将要举办“文学名著阅读分享大赛”,某校要从男生小明、小强和女生小慧、小红中共选取2人参加全区比赛,规定其中女生选n名.
(1)当_______时,“男生小明参加”是必然事件.
(2)当时,小明和小慧同时参加比赛的概率是多少？(要求列出树状图或者表格)
19．如图,是的弦,点D是的中点,连接并反向延长交于点C.若,求的半径.
20．2024巴黎奥运会,郑钦文获得了网球女单的冠军,创造了历史时刻,也在国内批起一股网球热.某市准备为青少年举行一次网球知识讲座,小明的爸爸买到一张门票,但小明和妹妹都想去,那么谁去就成了问题,小明想到一个办法：他拿出一个装有质地、大小相同的个红球与个白球的袋子,让爸爸摸出一个球,如果摸出的是红球,妹妹去听讲座,如果摸出的是白球,小明去听讲座.
(1)爸爸说这个办法不公平,请你用概率的知识解释原因；
(2)若爸爸发现将袋子里的2个白球换成红球,然后用小明提出的办法来确定谁去听讲座就是公平的,问袋子中原来有红球和白球各有几个？
21．已知抛物线,若将该函数向先左平移1个单位,再向上平移9个单位,顶点恰好落在原点上.
(1)求抛物线的函数表达式和顶点坐标；
(2)若有一直线l与抛物线交于点,,且.若点P在抛物线上且在直线l下方,且点P不与点A,B重合,分别求出点P横坐标与纵坐标的取值范围.
22．如图,为的直径,内接于,,交于点E.
(1)求的度数；
(2)若E为的中点,,求直径的长.
23．某企业生产甲、乙两种产品,根据市场调查与预测,甲产品的利润与投资金额成正比；乙产品的利润与投资金额成二次函数关系,其关系如图：其中点A、B、C的坐标分别为,,.
(1)分别求出甲,乙两种产品的利润与投资之间的关系式；
(2)若该企业将资金全力投入乙产品的生产,至少要投入多少资金才能使企业获利；
(3)该企业准备筹集a万元投入甲,乙两种产品的生产,且该企业计划两种产品最小利润不低于资金额的,那么该企业至少要筹集到多少资金？
24．已知,是的直径,点C为圆上一点,点D,E分别为弧,弧的中点,过点E作于点F,点D,G关于直线对称,连接.
(1)求弧的度数；
(2)若为的直径,请猜想与的数量关系,并给出证明；
(3)设,的面积为S,若的半径为1,求S关于x的函数解析式.
参考答案
1．答案：C
解析：选项A,B,D中的图形将其按顺时针方向旋转后,图形都发生变化,
把选项C中的图形将其按顺时针方向旋转后得到的图形不变,
故选：C.
2．答案：A
解析：二次函数的一次项系数是
故选：A.
3．答案：D
解析：根据题意可得,原点坐标为,
∴A、当时,,该函数图象不经过原点,不符合题意；
B、当时,,该函数图象不经过原点,不符合题意；
C、当时,,该函数图象不经过原点,不符合题意；
D、当时,,该函数图象经过原点,符合题意；
故选：D.
4．答案：D
解析：∵点A,B,C在上,,
∴.
故选：D.
5．答案：C
解析：A.盒子里不一定都是红球,故该选项不正确,不符合题意；
B.他第6次摸到的不一定还是红球,故该选项不正确,不符合题意；
C.他第6次摸到的可能还是红球,故该选项正确,符合题意；
D.盒子里不一定还有其他颜色的球,故该选项不正确,不符合题意；
故选：C.
6．答案：B
解析：在平面直角坐标系中,将二次函数向左平移2个单位,所得函数的解析式为,
故选：B.
7．答案：A
解析：∵喷泉到花坛三个顶点的距离相等,
∴喷泉为三角形的花坛三边的垂直平分线的交点,即外心,
故选：A.
8．答案：A
解析：以量角器的直径为斜边作,设半圆弧的圆心为O,于点E,连接,
根据题意得,点B在圆O上,
,
于点E,
,
,
故选：A.
9．答案：B
解析：由二次函数,则它的对称轴为,开口向上,
∴图象上的点离对称轴越远则y的值越大,
∵,,,
∴,
∴,
故选：B.
10．答案：B
解析：根据图示可得,二次函数图象开口向下,对称轴直线为,
∴,,
∴,
二次函数图象与y轴交于正半轴,
∴,
二次函数图像经过点,
∴当时,,
∴,
∴A、,正确,不符合题意；
B、二次函数图像经过点,对称轴为直线,
∴二次函数图象经过的另一个点为,
∴设解析式为,
∴当时,函数的最大值为,
∵,
∴,
∴二次函数与直线,有两个交点,如图所示,
∴当时,关于x的方程有两个不相等的实数根,故该选项错误,符合题意；
C、∵,,
∴,该选项正确,不符合题意；
D、联立方程组得,,
∴,
整理得,,
∵,
∴,
∴,
∴直线与该函数必有两个交点,该项正确,不符合题意；
故选：B.
11．答案：
解析：的顶点坐标为,
故答案为：.
12．答案：
解析：从,0,这三个数中,是无理数,从3个数中选择,由2种结果,
∴随机选择一个数,则这个数为无理数的概率为,
故答案为：.
13．答案：/30度
解析：由旋转的性质得：,
∵,
∴.
故答案为：.
14．答案：4或2
解析：①当点P在圆内时,的直径长为,半径为；
②当点P在圆外时,的直径长为,半径为；
综上所述：的半径长为或.
故答案为：4或2.
15．答案：/
解析：设,则,
∴,,,
∴抛物线的对称轴直线为,
∴,
∴,,,,,
如图所示,连接,,
∵是半圆的直径,
∴,
∴,
∴,
∴,
∴,
∴(负值舍去),
∴,
故答案为：.
16．答案：4；
解析：连接,,设于交于点P,过点F作于P,如图所示：
∵是半圆的直径,点F是弧上的中点,
∴,
∵,
∴,,
∵为的角平分线,
∴,
∴,
∴是等腰直角三角形,
∴,
∴,即,
在中,,
由勾股定理得：,
∴,
∴,
∵,
∴,
∵点F是弧上的中点,
根据垂径定理得：,,
∴,
∵,,
∴,
∴,
故答案为：4,.
17．答案：(1)；函数图象的开口向下
(2)不在此函数图象上
解析：(1)由题意,点在函数图象上,
.
.
函数为.
∴函数图象的开口向下.
(2)由题意,抛物线为,
当时,.
点不在此函数图象上.
18．答案：(1)0
(2)
解析：(1)当时,即从男生小明、小强中选取2人参加全区比赛,则小明必然参加,
∴“男生小明参加”是必然事件,
故答案为：0；
(2)当时,选取2人参加全区比赛中有1名女生,把所有等可能结果表示如下,
有1名女生参加的共有4种等可能结果,其中有小明和小慧同时参加的结果有1种,
∴小明和小慧同时参加比赛的概率是.
19．答案：
解析：如图,连接,
设的半径为r,则,,
∵点D是的中点,是过圆心O的直线,
∴,,
在中,由勾股定理得,
即,解得,
∴的半径为.
20．答案：(1)见解析
(2)原来有红球8个,白球有个
解析：(1)∵个红球与个白球
∴摸出的是红球的概率为
摸出的是白球的概率为,
,
∴这个办法不公平.
(2)依题意,
解得：
是原方程的解,
则,,
∴原来有红球8个,白球有12个
21．答案：(1),顶点坐标为
(2)点P横坐标的取值范围为,纵坐标的取值范围为
解析：(1)∵抛物线,
∴将该函数向先左平移1个单位,再向上平移9个单位,可得抛物线为：,
∵顶点恰好落在原点上,
∴,
解得：,
∴为；
∴顶点坐标为；
(2)根据题意可得,当时,.
当时,,
解得,.
∵,
∴.
∴,,
∵点P在抛物线上且在直线l下方(不与点A,B重合),,如图,
∴抛物线开口向上,当时函数取得最小值,
∴,
∵当时,,当时,,
∴,
∴点P横坐标的取值范围为,纵坐标的取值范围为.
22．答案：(1)
(2)
解析：(1)∵所对的圆周角是,所对的圆心角是,
∴,
∵,
∴是等边三角形,
∴；
(2)如图所示,过点O作于点F,
∵是等边三角形,
∴是的中线,,
∴,,
∴,
设,则,
在中,,
∵点E为的中点,
∴,
∵,
∴,
∴,
在中,,
∴,
解得,(负值舍去),
∴,
∴.
23．答案：(1)；
(2)该企业将资金全力投入乙产品的生产,至少要投入超过12万元资金才能使企业获利
(3)该企业至少要筹集到80万元资金
解析：(1)由题意,设甲产品的利润为：,
∵在函数图象上,
∴,解得：,
∴甲产品的利润与投资之间的关系式为；
设乙产品的利润与投资金额x的函数关系为：
将,代入得,
解得：
∴,
(2)当时,,
解得：,.
∴该企业将资金全力投入乙产品的生产,至少要投入超过万元资金才能使企业获利；
(3)设该企业准备筹集x万元投入乙两种产品的生产,则投入甲种产品的资金为万元,设总利润为y万元,
∴
函数y的对称轴为直线,
当时,,
∴,
解得：,
答：该企业至少要筹集到80万元资金.
24．答案：(1)弧的度数为
(2),证明见解析
(3)
解析：(1)如图,连接,,
∵是的直径,点C为圆上一点,
∴,
∵点D,E分别为弧,弧的中点,
∴,,
∴,
∴弧的度数为；
(2),理由如下：
如图,连接,,
∵为直径,
∴,
∵D,G关于对称,
∴,
∵,
∴,
∵,,
∴,,
∴,,
∴；
(3)如图,过E作于M,连接,,记,的交点为H,
由(1)可得：,
∴,,
∴为等腰直角三角形,
∴,
∵,
∴四边形是矩形,,
∴,,
∵,
∴,
∴,
设,
∴,
∵,
∴,
∴,
解得：或(舍去)
∴
.
∴.