第16课时 二次函数的实际应用 -【备战中考】2025年中考数学一轮总复习课件

这是一份第16课时 二次函数的实际应用 -【备战中考】2025年中考数学一轮总复习课件，共25页。PPT课件主要包含了名师点津等内容，欢迎下载使用。
知识点 二次函数的实际应用问题常见 类型
（1）利用抛物线顶点坐标来求最值；
（2）最值不在抛物线顶点处取得；
（3）分段函数求最值问题；
（4）复合函数求最值问题；
（5）借助二次函数图象解一元二次不 等式.
1. 若自变量之和为10的两个函数y1和y2 组成一个复合函数，若设y1的自变量为 x，则y2的自变量为10－x.
2. 借助二次函数图象解一元二次不等式 的关键是数形结合.
3. 最大值不在抛物线顶点处取得，可能 有以下两种情况：
4. 分段函数的最大值问题，需要分别求 出每段函数的最大值，然后在最大值当 中再选最大的.
考点一　二次函数区间最值
例1　 求下列函数的最值：
（1）y＝2（x－3）2＋4（2≤x≤5）；
[答案] 解：（1）当x＝3时，y取最小值4；当x＝2时，y＝6；当x＝5时，y＝12，∴y的最大值为12.
（2）y＝－2x2－16x＋3（－1≤x≤2）.
[答案] 解：（2）y＝－2x2－16x＋3＝ －2（x＋4）2＋35.当－1≤x≤2时，y随x的增大而减小，∴当x＝－1时，y取最大值17；当x＝2时，y取最小值－37.
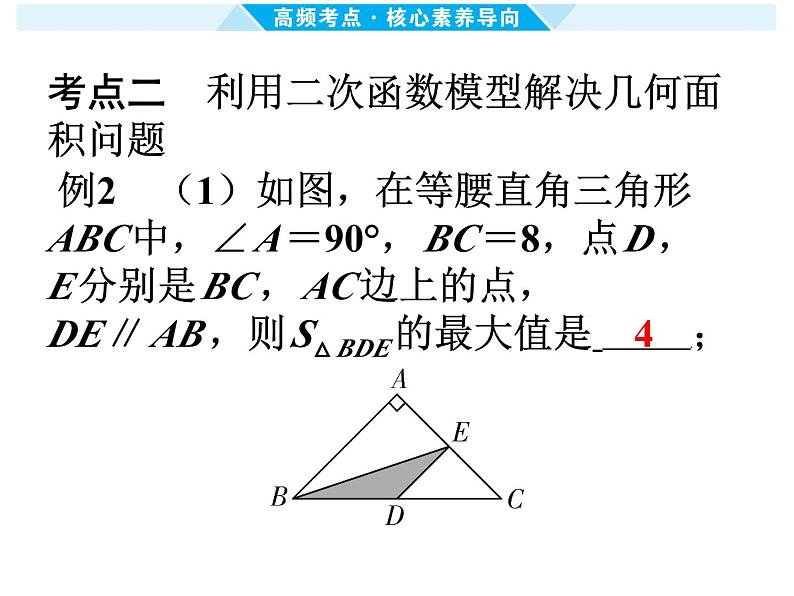
考点二　利用二次函数模型解决几何面 积问题
例2　（1）如图，在等腰直角三角形 ABC中，∠A＝90°，BC＝8，点D， E分别是BC，AC边上的点， DE∥AB，则S△BDE的最大值是 ⁠；
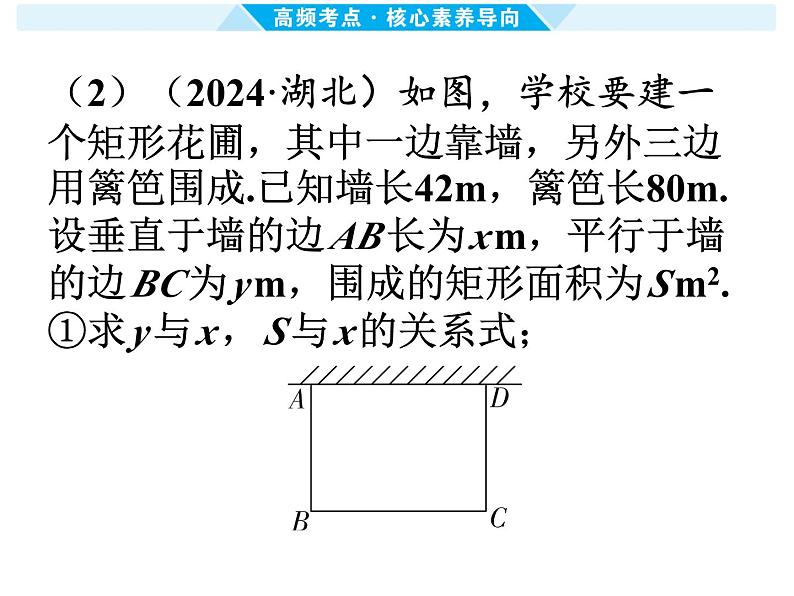
（2）（2024·湖北）如图，学校要建一 个矩形花圃，其中一边靠墙，另外三边 用篱笆围成.已知墙长42m，篱笆长80m. 设垂直于墙的边AB长为xm，平行于墙 的边BC为ym，围成的矩形面积为Sm2.①求y与x，S与x的关系式；
[答案] 解：①∵篱笆长80m，∴AB＋BC＋CD＝80m.∵AB＝CD＝xm，BC＝ym，∴x＋y＋x＝80，∴y＝80－2x.∵墙长42m，∴0＜80－2x≤42，解得19≤x＜40，∴y＝80－2x（19≤x＜40）.矩形面积S＝BC·AB＝y·x＝（80－ 2x）x＝－2x2＋80x（19≤x＜40）.
②围成的矩形花圃面积能否为750m2？ 若能，求出x的值；
[答案] 解：令S＝750，则－2x2＋80x＝750，整理，得x2－40x＋375＝0，
解得x1＝25，x2＝15.∵19≤x＜40，∴x＝25.∴当x＝25时，围成的矩形花圃面积为 750 m2.
③围成的矩形花圃面积是否存在最大 值？若存在，求出这个最大值，并求出 此时x的值.
[答案] 解： S＝－2x2＋80x＝－2（x－20）2＋800.∵－2＜0，∴S有最大值.又∵19≤x＜40，∴当x＝20时，S取得最大值，此时S＝ 800 m2.
考点三　利用二次函数模型解决实际 问题例3　 （2024·内江）端午节吃粽子是中 华民族的传统习俗.市场上猪肉粽的进价 比豆沙粽的进价每盒多20元，某商家用 5000元购进的猪肉粽盒数与3000元购进 的豆沙粽盒数相同.在销售中，该商家发 现猪肉粽每盒售价52元时，可售出180 盒；每盒售价提高1元时，少售出10盒.
（1）求这两种粽子的进价；
（2）设猪肉粽每盒售价x元 （52≤x≤70），y表示该商家销售猪肉粽 的利润（单位：元），求y关于x的函数 表达式并求出y的最大值.
考点四　抛物线的实际应用例4　 （1）（2024·天津）从地面竖直向 上抛出一小球，小球的高度h（m）与 小球的运动时间t（s）之间的关系式是 h＝30t－5t2（0≤t≤6）.有下列结论：①小球从抛出到落地需要6s；②小球运动中的高度可以是30m；③小球运动2s时的高度小于运动5 s时的 高度.
其中，正确结论的个数是（　C　）
（2）（2024·陕西）一条河上横跨着一 座宏伟壮观的悬索桥.桥梁的缆索L1与缆 索L2均呈抛物线型，桥塔AO与桥塔BC 均垂直于桥面，如图所示，以点O为原 点，以直线FF'为x轴，以桥塔AO所在 直线为y轴，建立平面直角坐标系.
已知：缆索L1所在抛物线与缆索L2所在 抛物线关于y轴对称，桥塔AO与桥塔 BC之间的距离OC＝100m，AO＝BC＝ 17m，缆索L1的最低点P到FF'的距离 PD＝2m.（桥塔的粗细忽略不计）
①求缆索L1所在抛物线的函数表达式；
②点E在缆索L2上，EF⊥FF'，且EF ＝2.6m，FO＜OD，求FO的长.
∴FO＝40m或FO＝60m，∵FO＜OD，∴FO的长为40m.
1. 用长12m的铝合金条制成矩形窗框 （如图所示），那么这个窗户的最大透 光面积是 m2.（中间横框所占的面 积忽略不计）
2. 某商厦将进货单价为70元的某种商 品，按销售单价100元出售时，每天能卖 出20个.通过市场调查发现，这种商品的 销售单价每降价1元，日销量就增加1个. 为了获取最大利润，这种商品的销售单 价应降 元.
4. （2024·河南）从地面竖直向上发射的 物体离地面的高度h（m）满足关系式h ＝－5t2＋v0t，其中t（s）是物体运动的 时间，v0（m/s）是物体被发射时的速 度.社团活动时，科学小组在实验楼前从 地面竖直向上发射小球.
（1）小球被发射后 s时离地面的 高度最大（用含v0的式子表示）；
（2）若小球离地面的最大高度为20m， 求小球被发射时的速度；