第19课时 全等三角形-【备战中考】2025年中考数学一轮总复习课件

这是一份第19课时 全等三角形-【备战中考】2025年中考数学一轮总复习课件，共44页。PPT课件主要包含了2中点模型，3手拉手模型，4含半角模型，5一线三等角模型，答案图，∵DM＝CM，答案图1等内容，欢迎下载使用。
知识点1 三角形全等的概念
能够完全重合的两个三角形叫做全 等三角形.
知识点2 全等三角形的性质
全等三角形的对应边 ⁠，对 应角 ⁠，对应线段（高、中线、 角平分线） ，周长、面积 ⁠⁠.
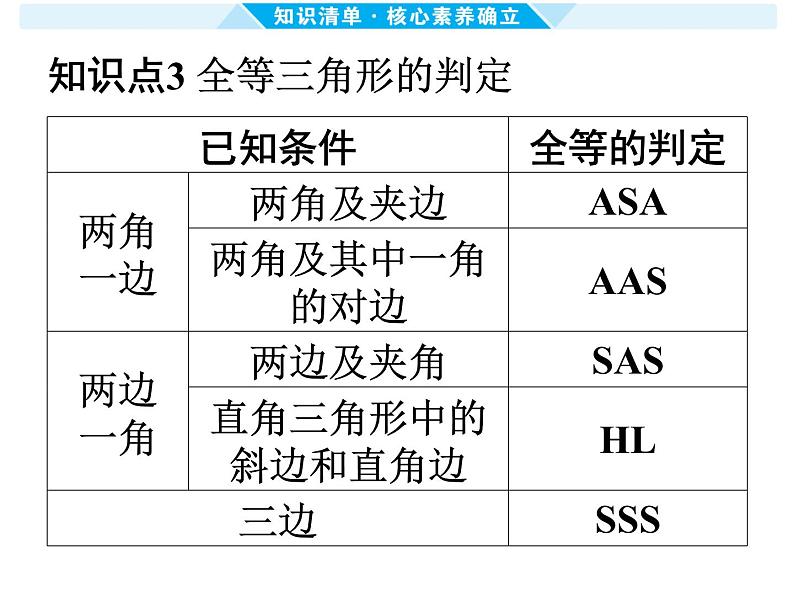
知识点3 全等三角形的判定
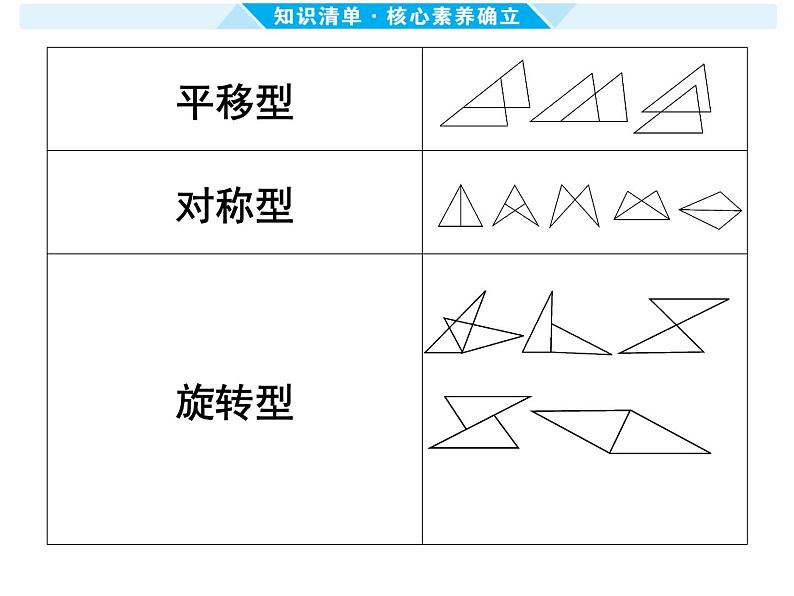
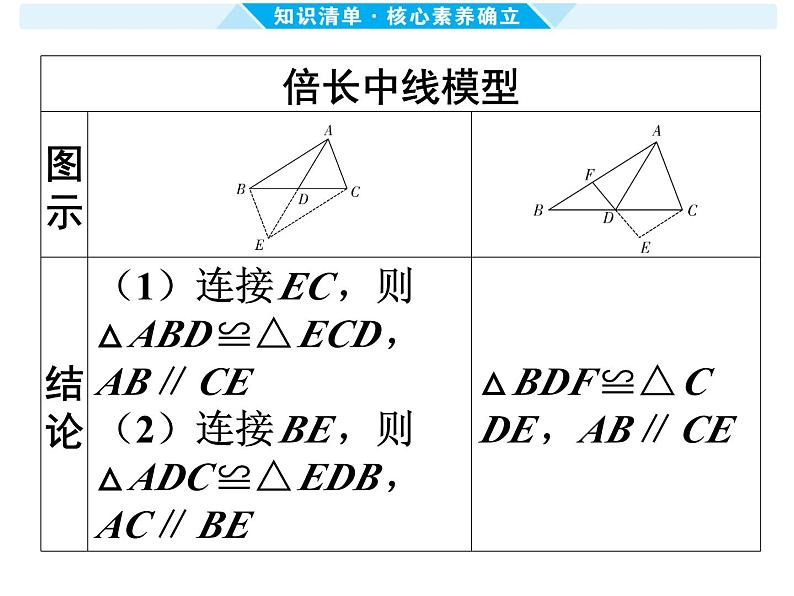
知识点4 全等的基本图形及结论【模型（2）－（5）针对练习见作业本 微专题十一】（1）平移、对称、旋转三 种基本模型
名师指津1. 全等三角形的判定定理本身容易理 解，但定理的灵活应用以及寻找定理需 要的条件有时比较困难.三角形全等是平 面几何中培养逻辑推理能力的重要手段.
2. 证明三角形全等的思路（1）已知两边：①找夹角（SAS）；② 找直角（HL）；③找第三边（SSS）.（2）已知一边和一角：①边为角的对 边，找任意一角（AAS）；②边为角的 邻边，找夹角的另一边（SAS）；找夹 边的另一角（ASA）；找边的对角 （AAS）.（3）已知两角：找夹边（ASA）或角的 对边（AAS）.
3. 寻找对应边、对应角的方法和规律：（1）有公共边的，公共边一定是对应 边；（2）有公共角的，公共角一定是对应 角；（3）有对顶角的，对顶角一定是对应 角；（4）两个全等三角形中一对最长（短） 的边（或最大、最小的角）一定是对应 边（角）.
考点一　全等三角形的性质
例1　 （1）如图1，△ABC≌△BDE， AB⊥BD，AC＝4，DE＝3，则CE的 长为（　A　）
（2）如图2，△ABC≌△ADE，线段 BC的延长线过点E，与线段AD交于点 F. 若∠AED＝108°，∠CAD＝12°， ∠B＝48°，则∠DEF的度数为 ⁠.
考点二　全等三角形的判定例2　 （1）（2024·八中）如图1是雨伞 在开合过程中某时刻的截面图，伞骨AB ＝AC，点D，E分别是AB，AC的中 点，DM，EM是连接弹簧和伞骨的支 架，且DM＝EM，已知弹簧M在向上 滑动的过程中，总有△ADM≌△AEM，其判定依据是（　C　）
（2）如图2，∠E＝∠F＝90°，∠B ＝∠C，AE＝AF，则下列结论：① ∠EAC＝∠FAB；②CM＝BN；③CD ＝DN；④△ACN≌△ABM. 其中正确 的有（　B　）
（3）如图3，AB＝4cm，AC＝BD＝ 3cm，∠CAB＝∠DBA，点P在线段 AB上以1cm/s的速度由点A向点B运动. 同时，点Q在线段BD上由点B向点D运 动.设运动时间为ts，则当△ACP与△BPQ全等时，点Q的运动速度为 ⁠⁠cm/s.
考点三　全等三角形的判定与性质例3　 如图，在△ABM中，∠ABM＝ 45°，AM⊥BM，垂足为M，C是BM 的延长线上一点，连接AC. 设D是线段 AM上一点，且MD＝MC，连接BD； E是△ABC外一点，且EC＝AC，连接 ED并延长交BC于点F，且F是线段BC 的中点.求证：∠BDF＝∠CEF.
[答案] 证明：延长EF到点G，使得FG＝EF，连接BG，如答案图所示.
∵AM⊥BM，∠ABM＝45°，
∴∠BMD＝∠AMC＝90°，BM＝AM.
∴△BMD≌△AMC（SAS），∴BD＝AC.
又∵CE＝AC，∴BD＝CE.
∵F是线段BC的中点，∴BF＝CF.
∵∠BFG＝∠CFE，FG＝FE，
∴△BFG≌△CFE（SAS），
∴BG＝CE，∠G＝∠CEF，
∴BD＝CE＝BG，∴∠BDF＝∠G＝ ∠CEF.
例4　 （2024·南开）如图，在Rt△ABC 中，∠ACB＝90°，BC＜AC，过点B 作DE∥AC，且BD＝BC，过点B作 BF⊥AB交CD于点F，连接EF.

图1 图2
（1）如图1，若∠BAC＝40°，且BF＝BE，求∠CFE的度数；
图1
（2）如图2，若DE＝AC，求证：AB ＝BF＋EF.
1. 如图，在△ABC和△DEF中，AB＝ DE，BC＝EF. 添加下列条件，仍不能 确定△ABC≌△DEF的是（　B　）
2. （2024·一中）如图，在Rt△ABC中， ∠BAC＝90°，AB＝AC，MN是过点 A的直线，BD⊥MN于点D，CE⊥MN 于点E. 若BD＝4，CE＝6，则DE的长 为 ⁠.
3. 如图，在△ABC中，∠ABC＝90°， AB＝BC，点D是AC的中点，点E在 CD上（点E不与点D和点C重合）， AG⊥BE于点G，交BD于点F，连接 DG. （1）求证：△ADF≌△BDE；
解：（1）证明：∵AB＝BC，点D是AC的中点，∴∠ADF＝∠BDE＝90°，∴∠DAF＋∠AFD＝90°.∵AG⊥BE，∴∠BFG＋∠DBE＝90°.∵∠AFD＝∠BFG， ∴∠DAF＝∠DBE. ∵∠ABC＝90°，点D是AC的中点，∴AD＝BD，∴△ADF≌△BDE（ASA）.
（1）求证：△ADF≌△BDE；
（2）若DF＝3，GE＝4，求GF的长；
（3）找出线段GF，GE，GD之间的数 量关系.