第29课时 轴对称与中心对称-【备战中考】2025年中考数学一轮总复习课件

这是一份第29课时 轴对称与中心对称-【备战中考】2025年中考数学一轮总复习课件，共22页。
知识点1 轴对称与中心对称的定义及性 质
对应线段
　　中心对称的定义中心对称：把一个图形绕着某一点 旋转 ⁠后能与另一个图形重合， 那么就说这两个图形关于这一点成中心 对称，这个点叫做 .关于某 点成中心对称的两个图形，对称点的连 线都经过对称中心，并且被对称中 心 ⁠.
　　中心对称图形：把一个图形绕着某 一点旋转 ⁠后，能与原来位置的 图形重合，这个图形就叫做中心对称图 形，这个点就是它的对称中心.
知识点2 平面直角坐标系中点的对称规 律平面内点A的坐标为（x，y），则（1）点A关于x轴对称的点的坐标 为 ⁠；（2）点A关于y轴对称的点的坐标 为 ⁠；（3）点A关于原点对称的点的坐标 为 ⁠.
名师指津1. 解决折叠问题的关键是找图形在折叠 过程中的不变量，利用勾股定理建立方 程，求线段长度.2. 在几何图形中求线段和的最小值往往 转化成两点之间线段最短或垂线段最短 等来解决，具体方法是利用轴对称，实 现化折为直.常见模型：将军饮马问题、过河修桥问 题、瓜豆问题、胡不归问题等.
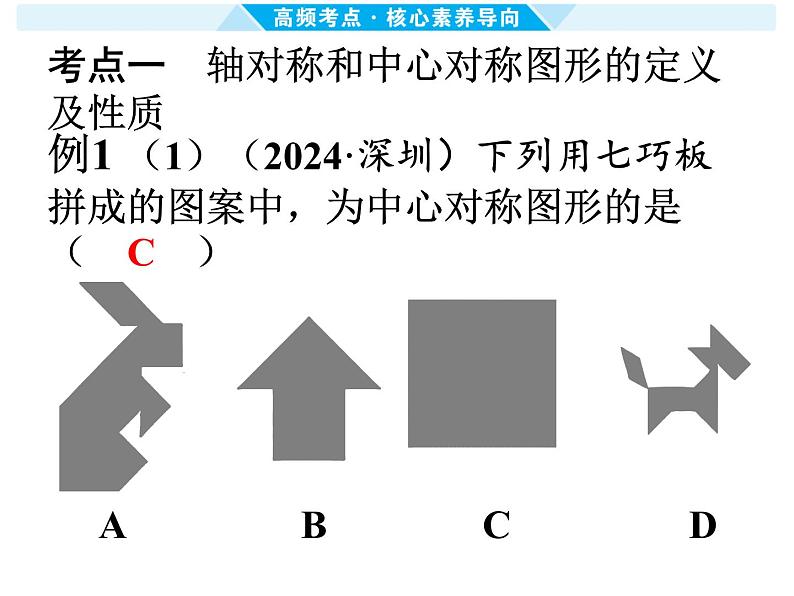
考点一　轴对称和中心对称图形的定义 及性质
例1 （1）（2024·深圳）下列用七巧板 拼成的图案中，为中心对称图形的是 （　C　）

A B C D
（2）（2024·泰安）下列图形中，是中 心对称图形的个数有（　C　）
（3）（2024·福建）小明用两个全等的 等腰三角形设计了一个“蝴蝶”的平面图 案.如图，其中△OAB与△ODC都是等腰 三角形，且它们关于直线l对称，点E， F分别是底边AB，CD的中点， OE⊥OF. 下列推断错误的是（　B　）
考点二　平面直角坐标系中点的对称与 最短路径例2　 （1）如图1，在平面直角坐标系 xOy中，△ABC关于直线y＝1对称，已 知点A的坐标是（4，4），则点B的坐 标是（　C　）
（2）（2024·青海）如图2，一次函数y ＝2x－3的图象与x轴相交于点A，则点 A关于y轴的对称点是 ⁠.
例3　 （1）（2024·广安）如图1，在 ▱ABCD中，AB＝4，AD＝5，∠ABC ＝30°，点M为直线BC上一动点，则 MA＋MD的最小值为 ⁠；
（2）如图2，点P是∠AOB内部任意一 点，OP＝5cm，点M和点N分别是射线 OA和射线OB上的动点，∠AOB＝30°，则△PMN周长的最小值为 cm；
（3）如图3，在边长为2的等边△ABC 中，D是BC边的中点，点E在线段AD 上，连接BE. 在BE的下方作等边△BEF，连接DF. 当△BDF的周长最小 时，∠DBF的度数是 ⁠.
考点三　图形的折叠例4　 （1）如图1，在△ABC中，∠A ＝22°，D为AB边中点，E为AC边上 一点，将△ADE沿着DE翻折，得到 △A'DE，连接A'B. 当A'B＝A'D时， ∠A'EC的度数为 ⁠；
（2）如图2，在三角形纸片ABC中， AB＝AC，∠B＝20°，点D是边BC上 的动点，将三角形纸片沿AD对折，使 点B落在点B'处，当B'D⊥BC时， ∠BAD的度数为 ⁠；
图3
1. （2024·成都）在平面直角坐标系xOy 中，点P（1，－4）关于原点对称的点 的坐标是（　B　）
2. 垃圾分类功在当代，利在千秋，下列 垃圾分类指引标志图形中，既是轴对称 图形又是中心对称图形的是（　D　）

A B C D
3. 如图，在四边形ABCD中，∠BAD＝ 140°，∠B＝∠D＝90°，在直线 BC，DC上分别找一点M，N，使得 △AMN的周长最小，则此时∠MAN的 度数为 ⁠.