陕西省宝鸡市陈仓区2023-2024学年八年级上学期期末考试数学试卷(含答案)

这是一份陕西省宝鸡市陈仓区2023-2024学年八年级上学期期末考试数学试卷(含答案)，共11页。试卷主要包含了选择题，填空题等内容，欢迎下载使用。
2023-2024学年度第一学期期末质量检测试题（卷）八年级数学
（时间：120分钟 满分：120分）
一、选择题（共24分）
1．9的算术平方根是（ ）
A．3B．﹣3C．81D．﹣81
2．下列各式中，计算正确的是（ ）
A．B．C．D．
3．如图，AB∥CD.若∠1＝40°，∠2＝65°，则∠CAD＝（ ）
A．50°B．65°C．75°D．85°
4．下列条件不能判断一个三角形是直角三角形的是（ ）
A．三个角的比为B．三条边满足关系
C．三条边的比为D．三个角满足关系
5．《义务教育课程标准（2022年版）》首次把学生学会炒菜纳入劳动教育课程，并作出明确规定．某班有7名学生已经学会炒的菜品的种数依次为：2，4，3，2，5，2，3．则这组数据的众数和中位数分别是（ ）
A．2，2B．2，2.5C．2，3D．3，3
6．如图所示，由下列条件能判定的是（ ）
A．B．
C．D．
7．某校课外小组的学生分组做课外活动，若每组7人，则余下3人：若每组8人，则少5人．设课外小组的人数为，应分成的组数为，可列方程组（ ）
A．B．C．D．
8．关于一次函数，下列结论正确的是（ ）
A．图象不经过第二象限
B．图象与轴的交点是
C．将一次函数的图象向左平移3个单位长度后，所得图象的函数表达式为
D．点和在一次函数的图象上，若，则
二、填空题（共12分）
9．比较大小：3 （填＜，＞或＝）．
10．设，为实数，且，则点在第 象限．
11．如图，直线：与直线：相交于点，则关于，的方程组的解为 ．
12．已知直线上的点到两坐标轴的距离相等，则点的坐标是 ．
三.解答题（共84分）
13．计算：
(1)；
(2)．
14．解方程组：
(1)
(2)
15．已知的平方根是，的立方根是3．
(1)求，的值；
(2)求的算术平方根．
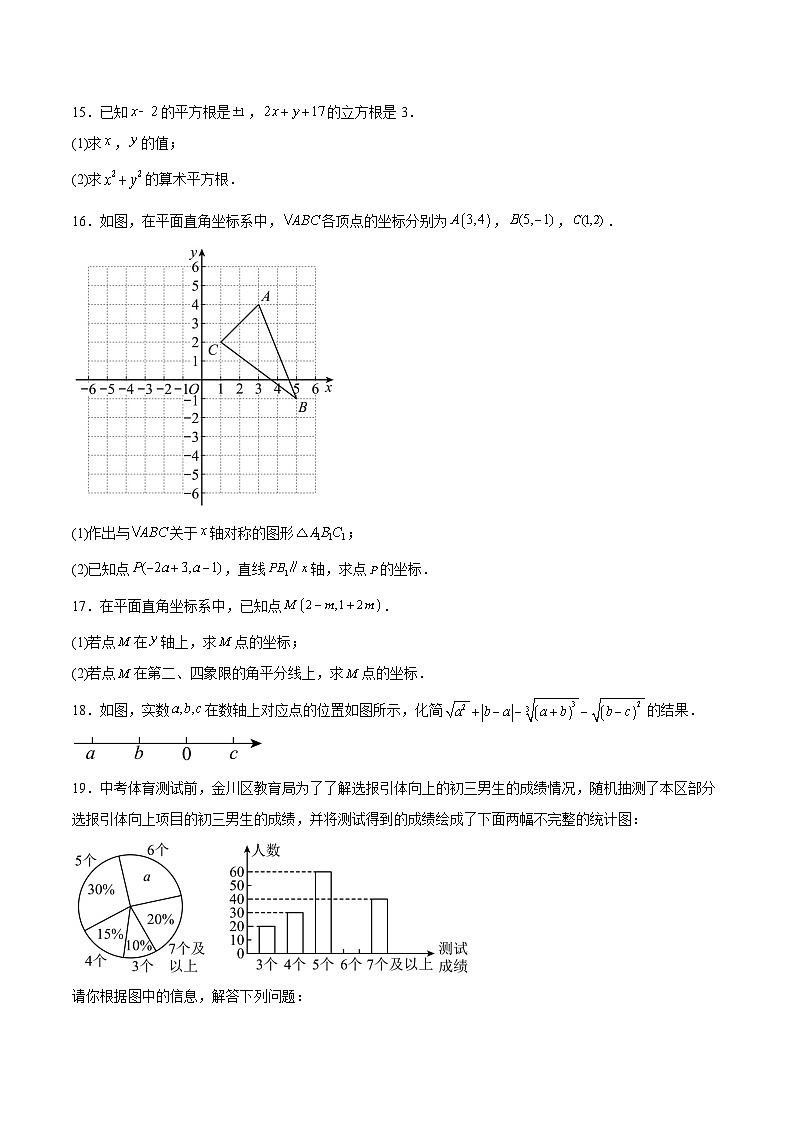
16．如图，在平面直角坐标系中，各顶点的坐标分别为，，．
(1)作出与关于轴对称的图形；
(2)已知点，直线轴，求点的坐标．
17．在平面直角坐标系中，已知点．
(1)若点在轴上，求点的坐标；
(2)若点在第二、四象限的角平分线上，求点的坐标．
18．如图，实数在数轴上对应点的位置如图所示，化简的结果．
19．中考体育测试前，金川区教育局为了了解选报引体向上的初三男生的成绩情况，随机抽测了本区部分选报引体向上项目的初三男生的成绩，并将测试得到的成绩绘成了下面两幅不完整的统计图：
请你根据图中的信息，解答下列问题：
(1)扇形统计图中a＝ %，并补全条形统计图．
(2)在这次抽测中，测试成绩的众数和中位数分别是 个、 个．
(3)该区体育中考选报引体向上的男生共有1800人，如果体育中考引体向上达6个以上（含6个）得满分，请你估计该区体育中考中选报引体向上的男生能获得满分的有多少名？
20．如图，在中，平分，交边于点E，在边上取点F，连接，使．
(1)求证：
(2)当，时，求的度数．
21．某市出租车收费标准如下：3千米以内（含3千米）收费11元；超过3千米的部分，每千米收费3元．
(1)写出应收车费，（元）与出租车行驶路程（千米）之间的关系式（其中）；
(2)小明从家到体育馆乘出租车行驶6千米应付多少元？
(3)小明从体育馆到图书馆乘出租车，付车费23元，从体育馆到图书馆出租车行驶了多少千米？
22．为了提高学生的身体素质，某校准备从某体育用品商店购买跳绳和毽子，已知购买50根跳绳和80个毽子共需1120元，购买30根跳绳和50个毽子共需680元．
(1)跳绳、毽子的单价各是多少元？
(2)八年级一班体育委员小明与二班体育委员小亮一起到该商店为本班学生购买跳绳，他俩共买了30根跳绳，小明说他比小亮少付了48元，你认为这可能吗？若可能，求出他们分别购买了几根跳绳：若不可能，请说明理由．（请用二元一次方程组求解）
23．直线：分别与，轴交于、两点，过点的直线交轴负半轴于，且．
(1)求点的坐标为__________；
(2)求直线的解析式；
(3)动点从出发沿射线方向运动，运动的速度为每秒个单位长度．设运动秒时，当为何值时为等腰三角形．（请直接写出的值）
参考答案与解析
1．A
2．D
3．C
4．C
5．C
6．D
7．B
8．C
9．＜
10．四
11．
12．或
13．(1)
(2)
（1）解：原式；
（2）解：原式．
14．(1)
(2)
（1）解：，
可得：，解得：，
将代入①可得：，解得：，
所以该不等式组的解集为：．
（2）解：化简为：，
可得：，解得：，
将代入②可得：，解得：．
所以该不等式组的解集为：．
15．(1)，
(2)5
（1）解：的平方根是，的立方根是3，
，，
解得：，；
（2）解：由（1）得：，，
，
的算术平方根为．
16．(1)见解析
(2)点的坐标为
（1）解：如图，即为所求．
（2），点与点关于轴对称，
．
，轴，
点的纵坐标为1，
，
，
，
点的坐标为．
17．(1)
(2)
（1）解：由题意得：，
∴，
（2）解：在第二、四象限的角平分线上，
，
，
．
18．
解：观察数轴得：，
．
19．(1)25，图见解析
(2)5，5
(3)810名
（1）解：扇形统计图中a=1-30%-15%-10%-20%=25%，
设引体向上6个的学生有x人，由题意得
，解得x=50．
条形统计图补充如下：
故答案为：5；
（2）解：由条形图可知，引体向上5个的学生有60人，人数最多，所以众数是5；
共200名同学，排序后第100名与第101名同学的成绩都是5个，故中位数为（5+5）÷2=5．
故答案为：5，5．
（3）解：（名）．
答：估计该区体育中考选报引体向上的男生能获得满分的同学有810名．
20．(1)见详解
(2)
（1）证明：∵平分，
∴，
又∵，
∴，
∴．
（2）∵，
∴
在中，，
∴，
又∵平分，
∴
∴．
21．(1)
(2)20元
(3)7千米
（1）解：由题意可得：当时，
；
（2）当时，（元）；
（3）当时，，
解得：；
答：从体育馆到图书馆出租车行驶了7千米．
22．(1)跳绳的单价为16元，毽子的单价为4元；
(2)这是不可能的，理由见解析．
（1）解：设跳绳的单价为元、毽子的单价为元，
根据题意得，
解得，
∴跳绳的单价为16元、毽子的单价为4元。
（2）解：设小明购买了根跳绳，小亮购买了根跳绳，
根据题意得，
解得，
由题意可知，为整数，
∴这是不可能的．
23．(1)
(2)
(3)（秒），（秒），（秒）时，为等腰三角形
（1）解：直线：分别与轴交于，
，
解得，
即函数解析式为，
当时，，
点坐标是，
故答案为；
（2），，
，
解得，
即，
设直线的解析式为，图像经过点，，
得，解得，
直线的解析式为．
（3）设点坐标，由勾股定理，得，
①当时， （秒），
即运动秒，为等腰三角形．
②当时，，即，
化简，得，
解得，
即．
，
（秒），
即运动秒时，为等腰三角形．
③当时，得，
即，
（秒），
即运动秒时，为等腰三角形，
综上所述：（秒），（秒），（秒）时，为等腰三角形．