初中数学人教版（2024）七年级下册（2024）第七章 相交线与平行线7.3 定义、命题、定理教课内容课件ppt

这是一份初中数学人教版（2024）七年级下册（2024）第七章 相交线与平行线7.3 定义、命题、定理教课内容课件ppt，共19页。PPT课件主要包含了什么叫定义，真命题，假命题，基本事实，一般举一个反例即可，归纳总结，证实其他命题的正确性，推理的过程叫证明，一些条件，典例精析等内容，欢迎下载使用。
1. 掌握定理的概念，并能分清命题与定理之间的关系.2. 了解证明的意义，知道要判断一个数学结论是否正确，仅仅依靠经验、观察或实验是不够的，必须一步一步、有理有据地进行推理.重点：掌握定理的概念，了解证明的意义.难点：掌握推理的方法和步骤.
我们举例的一些描述称为数学对象的定义，一个数学对象的定义揭示了它的本质特征，能够帮助我们准确地理解它，并作出准确的判断.
2. 命题的结构是什么?
数学中的命题常可以写成“如果……那么……”的形式，这时“如果”后接的部分是题设，“那么”后接的部分是结论.
用我们以前学过的观察,实验,验证特例等方法.
这些方法往往并不可靠.
那已经知道的真命题又是如何证实的?
能不能根据已经知道的真命题证实呢?
如何证实一个命题是真命题呢？
古希腊数学家欧几里得 (公元前 300 年前后) 编写了一本书，书名叫做《原本》. 为了说明每一结论的正确性，他在编写这本书时进行了大胆创造：挑选了一部分数学名词和一部分公认的真命题作为证实其他命题的出发点和依据.
讨论：判断下列命题哪些是真命题? 哪些是假命题?(1) 在同一平面内，如果一条直线垂直于两条平行线中的一条，那么也垂直于另一条；(2) 如果两个角互补，那么它们是邻补角；(3) 如果 | a | = | b |，那么 a = b；(4) 经过直线外一点有且只有一条直线与这条直线平行；(5) 两点确定一条直线.
上面练习中的(1)的正确性是经过推理证实的，这样得到的真命题叫作定理.定理也可以作为继续推理的依据.(4)(5)是真命题，属于基本事实.
(1) 在同一平面内，如果一条直线垂直于两条平行线中的一条，那么也垂直于另一条；(4) 经过直线外一点有且只有一条直线与这条直线平行；(5) 两点确定一条直线.
基本事实： 不需要证明. 除了基本事实外，其他真命题的正确性都需要通过演绎推理的方法证实.
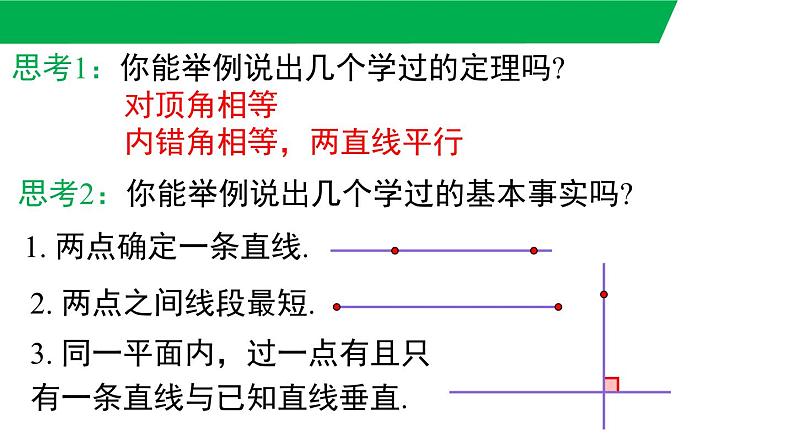
思考2：你能举例说出几个学过的基本事实吗?
3. 同一平面内，过一点有且只有一条直线与已知直线垂直.
2. 两点之间线段最短.
1. 两点确定一条直线.
对顶角相等内错角相等，两直线平行
思考1：你能举例说出几个学过的定理吗?
4. 两条直线被第三条直线所截，如果同位角相等，那么这两条直线平行 (简述为：同位角相等，两直线平行).
5. 过直线外一点有且只有一条直线与这条直线平行.
讨论：前面我们学习了命题、定理，现在我们来学习证明，命题、定理和证明之间有什么联系和区别?
在很多情况下，一个命题的正确性需要经过推理，才能作出判断，这个推理过程叫作证明.
基本事实是定理推导的起点，无需证明但被广泛接受为真.
定理是命题和基本事实的逻辑延伸，通过证明得到的真命题.
定义，命题，基本事实，定理之间的区别与联系：
定义是命题、基本事实和定理的基础，明确了它们的讨论范围.
经过证明的真命题叫定理
例1 如图，已知直线 a⊥b，b∥c，求证：a⊥c．
证明：∵ a⊥b(已知)， ∴ ∠1 = 90°(垂直的定义).又 ∵ b∥c(已知)，∴∠2 =∠1 = 90°(两直线平行，同位角相等).∴ a⊥c(垂直的定义).
例2 如图，给出下列论断：(1) AB∥DC，(2)AD∥BC，(3) ∠A +∠ABC = 180°，(4)∠ABC +∠C = 180°，以其中一个作为题设，另一个作为结论，写出一个真命题.想一想，若连接 BD，你能试着写出一个真命题并写出其推理过程吗?
如果 AB∥DC，那么∠ABC +∠C = 180°.
如果 AB∥DC，那么∠ABD =∠BDC.
思考：证明需要注意些什么?
证明中的每一步推理都要有根据，这些根据可以是已知条件，也可以是学过的定义、基本事实、定理等.
证明：∵AB∥DC(已知)，∴∠ABD =∠BDC(两直线平行，内错角相等).
1. 请把下面证明过程补充完整.如图，已知 AD⊥BC 于点 D，点 E 在 BA 的延长线上，EG⊥BC 于点 G，交 AC 于点 F，∠E =∠1.求证：AD 平分∠BAC.
证明：∵AD⊥BC，EG⊥BC，∴∠ADC = ∠EGC = 90°( ).∴ AD∥EG ( ).∴∠1=∠2( )，∠E =∠3( ).∵∠E =∠ (已知)，∴∠2 =∠3( ).∴AD 平分∠BAC ( ).
同位角相等，两直线平行
两直线平行，内错角相等
两直线平行，同位角相等
2. 如图，现有以下 3 个论断：①AB∥CD；②∠B =∠C；③∠E =∠F. 请以其中 2 个论断为条件，另一个论断为结论构造命题.(1) 你构造的是哪几个命题?(2) 请选择其中一个真命题加以证明.
解：(1)由①②得③；由①③得②； 由②③得①.(2) 由①②得③，证明过程如下：∵ AB∥CD，∴∠EAB =∠C.又∵∠B =∠C，∴∠EAB = ∠B.∴CE∥BF. ∴∠E =∠F. (答案不唯一)