数学人教版（2024）7.2.3 平行线的性质评课ppt课件

这是一份数学人教版（2024）7.2.3 平行线的性质评课ppt课件，共22页。PPT课件主要包含了随堂练习，课堂小结，内错角，同位角，两条直线平行，同旁内角，角之间的关系，∠1∠2，AB∥EF，CD⊥BF等内容，欢迎下载使用。
1.掌握平行线的性质与判定的综合运用；(重点)2.体会平行线的性质与判定的区别与联系.(难点)
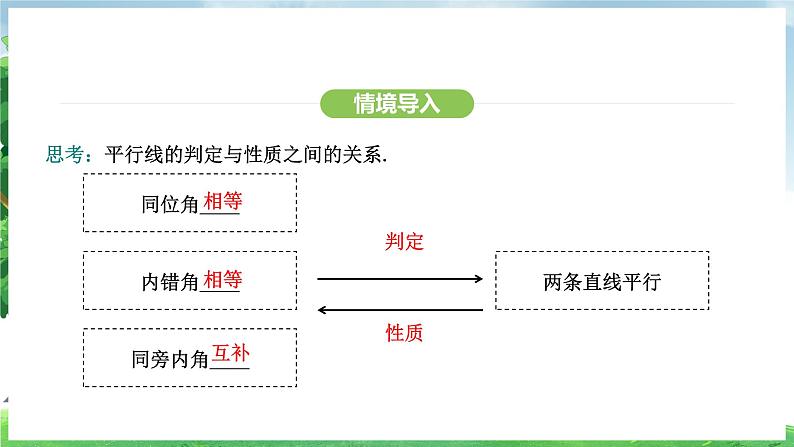
思考：平行线的判定与性质之间的关系.
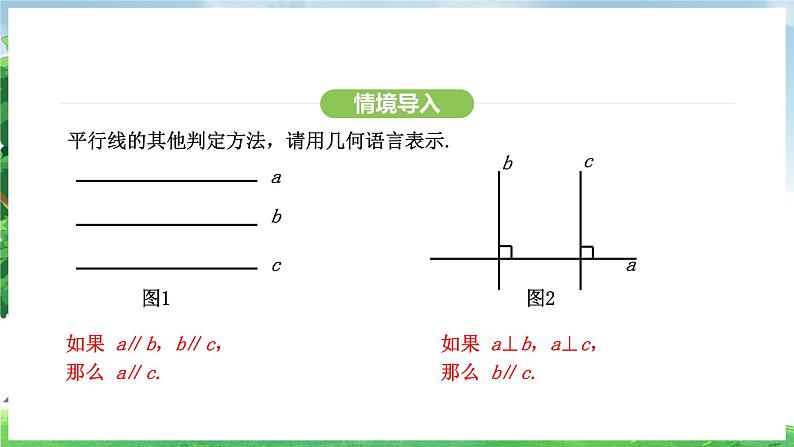
平行线的其他判定方法，请用几何语言表示.
如果 a∥b，b∥c，那么 a∥c.
如果 a⊥b，a⊥c，那么 b∥c.
知识点一 平行线的性质和判定的综合运用
例1 如图，若∠1 = ∠3，∠2 = 60° ，则 ∠4 的度数为( )
A.60° B.100° C.120°D.130°
∵∠1 = ∠3，∴a∥b(内错角相等，两直线平行).∴∠2+∠5=180°(两直线平行，同旁内角互补).∵∠4=∠5，∠2 = 60°，∴∠4=∠5=180°-∠2=120°.
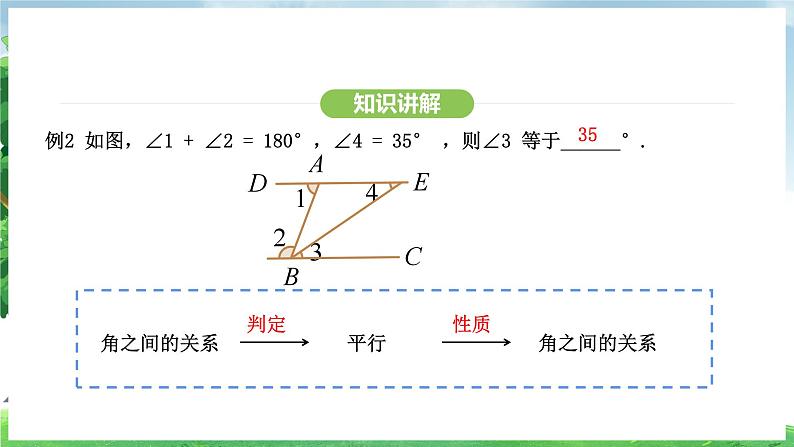
例2 如图，∠1 + ∠2 = 180°，∠4 = 35° ，则∠3 等于______°.
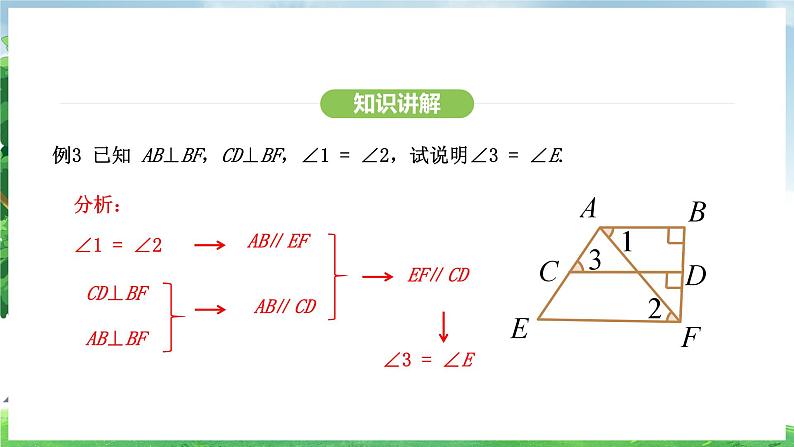
例3 已知 AB⊥BF，CD⊥BF，∠1 = ∠2，试说明∠3 = ∠E.
解：∵∠1 = ∠2 (已知)，∴ AB∥EF (内错角相等，两直线平行).∵ AB⊥BF，CD⊥BF， ∴ AB∥CD(垂直于同一条直线的两条直线平行).∴ EF∥CD(平行于同一条直线的两条直线平行). ∴∠3 = ∠E (两直线平行，同位角相等).
例4 如图，∠1 = ∠2，∠E = ∠F ，判断 AB 与 CD 的位置关系 ，说明理由.
与两条直线相截的第三条直线
延长 BE 交 DC 的延长线于M
解：AB∥CD，理由如下： 如图，延长 BE 交 DC 的延长线于点 M， ∵∠BEF = ∠F，∴BM∥FC. ∴∠M = ∠2. ∵∠1 = ∠2， ∴∠M = ∠1. ∴AB∥CD.
例5 如图，已知CE⊥AB,MN⊥AB,∠EDC+∠ACB=180°.试说明：∠1=∠2.
需说明 ∠2=∠BCE
需说明 ∠1=∠BCE
解：∵CE⊥AB,MN⊥AB,∴MN∥CE, ∴∠2=∠BCE. ∵∠EDC+∠ACB=180°, ∴ED//BC，∴∠1=∠BCE,∴∠1=∠2.
思路点拨：本例中要说明两个角相等，可借助平行线的性质，通过第三个角进行等角转化.
1.如图，DA⊥AB，CD⊥DA，∠B = 56° ，则∠C 的度数为 ( )
A.154°B.144°C.134°D.124°
2. 如图，C、D 是直线 AB 上的两点，∠1+∠2 = 180°，DE 平分∠CDF ，EF∥AB.(1) CE 与 DF 平行吗？为什么？(2) 若∠DCE = 130°，求∠DEF 的度数.
∠1+∠2 = 180°
∠1 +∠DCE = 180°
∠DCE = 130°
∠CDF = 50°
∠CDE = 25°
解：(1) CE∥DF，∵∠1 +∠2 = 180°，∠1 +∠DCE = 180°， ∴∠2 = ∠DCE. ∴CE∥DF.
3. 如图，EF∥AD，∠1 = ∠2，∠BAC = 70°，求∠AGD 的度数.
∠BAC +∠AGD = 180°
∠AGD = 110°
解：∵ EF∥AD，∴∠2 = ∠3. 又∵∠1 = ∠2， ∴∠1 = ∠3. ∴ DG∥AB. ∴∠BAC +∠AGD = 180°. ∴∠AGD = 180°-∠BAC = 180°- 70° = 110°.
4. 如图①，AB∥CD，E 是射线 FD 上的一点，∠ABC = 140°，∠CDF = 40° .(1) 试说明：BC∥EF；(2) 连接 BD，如图②.若∠BAE = 110°，BD∥AE，则BD 是否平分∠ABC ？ 请说明理由 .
解：(1)∵ AB∥CD，∴∠ABC +∠BCD = 180°. ∵∠ABC = 140°， ∴∠BCD = 40°. ∵∠CDF = 40°， ∴∠BCD = ∠CDF. ∴BC∥EF.
5.如图，∠1+∠2=180°.(1)试说明：AB//EF; (2)若CD平分∠ACB,∠DEF=∠A,∠BED=60°,求∠EDF的度数.
解：(1)∵∠1与∠EFD是邻补角，∴∠1+∠EFD=180°. 又∠1+∠2=180°, ∴∠2=∠EFD,∴AB//EF.