数学七年级下册（2024）8.2 立方根集体备课ppt课件

这是一份数学七年级下册（2024）8.2 立方根集体备课ppt课件，共24页。PPT课件主要包含了立方根的表示等内容，欢迎下载使用。
1.了解立方根的概念及性质，会用根号表示一个数的立方根；(重点)2.了解开立方与立方是互逆运算，会用开立方运算求一个数的立方根.(难点)
二阶魔方由几个小立方体构成______
三阶魔方由几个小立方体构成______
四阶魔方由几个小立方体构成______
如果一个魔方由 27 个小立方体构成，它应该是几阶魔方？
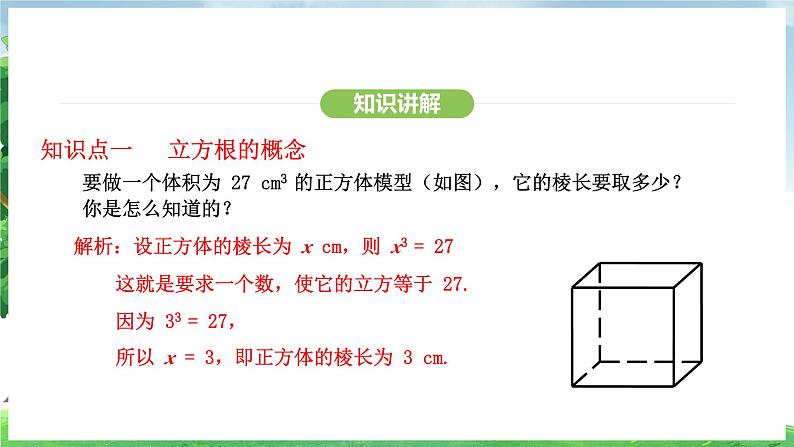
要做一个体积为 27 cm3 的正方体模型（如图），它的棱长要取多少？你是怎么知道的？
解析：设正方体的棱长为 x cm，则 x3 = 27
这就是要求一个数，使它的立方等于 27.
因为 33 = 27，
所以 x = 3，即正方体的棱长为 3 cm.
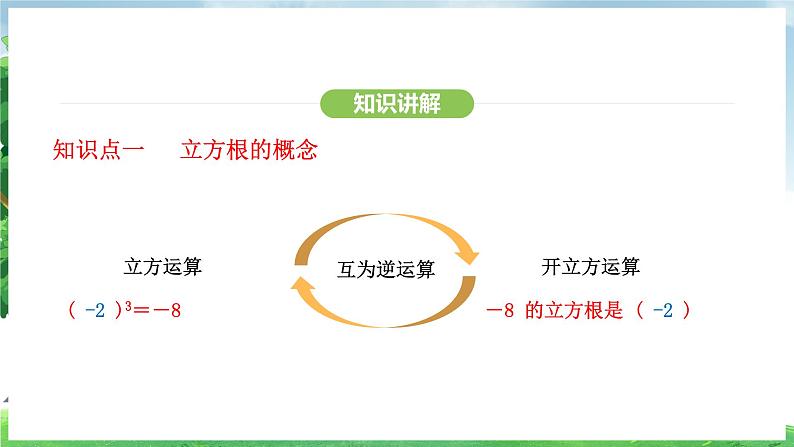
知识点一 立方根的概念
同学们能类比平方根的概念，给出立方根的概念吗？
一般地，如果一个数 x 的立方等于 a，即x3 = a，那么这个数 x 就叫作 a 的立方根，或三次方根．
根据立方根的定义填空：
因为( )3 = 0.125，所以 0.125 的立方根是 ( 　)；
因为( )3 ＝ 0，所以 0 的立方根是 ( 　)；
因为( )3 ＝ －8，所以 －8 的立方根是 ( 　)；
知识点二 立方根的性质
一个正数有一个正的立方根；一个负数有一个负的立方根，零的立方根是零.
立方根是它本身的数有 1，-1，0；平方根是它本身的数只有 0.
( )3＝5
如果正方体的体积为 5 cm3，那么其边长是多少？
思考：能否找到一个正数( x )来表示其边长？
类比于平方根，一个数 a 的立方根如何表示？
一个数 a 的立方根可以表示为
其中 a 是被开方数，3 是根指数，3 不能省略.
平方根与立方根的区别和联系
例1.求下列各数的立方根：
你能归纳出立方根的另一性质吗？
解析：原式 = 3 + 2 - (-1) = 5 + 1 = 6.
由于一个数的立方根可能是无限不循环小数，所以我们可以利用计算器求一个 数的立方根或它的近似值.
用计算器求下列各数的立方根：343， -1.331.
知识点三 用计算器求立方根
总结：被开方数的小数点向左或向右移动 3n 位时，立方根的小数点就相应的向左或向右移动 n 位 (n 为正整数).
解析：33 = 27，43 = 64.
因为 27 < 50 < 64，
3. 立方根概念的起源与几何中的正方体有关，如果一个正方体的体积为 V，那么这个正方体的边长为多少？
4. 一个长方体的长为 9 cm，宽为 3 cm，高为 4 cm，而另一个正方体的体积是它的二倍，求这个正方体的棱长.
解析：设正方体的棱长为 a cm， 则依题意得 a3 = 9×3×4×2 ， 解得 a = 6. 故这个正方体的棱长为 6 cm.
5. 已知一个正数的两个平方根分别为 a 和 (-2a - 5).(1) 求 a 的值，并求这个正数；(2) 求 34 + 2a3 的立方根.
解：(1) 由题意，得 a + (-2a - 5) = 0， 解得 a = -5，∴ 这个正数为 (-5)2 = 25.
(2) 34 + 2a3 = 34 + 2×(-5)3 = -216 ∴ 34 + 2a3 的立方根是 -6.