人教版（2024）七年级下册（2024）8.3 实数及其简单运算教学ppt课件

这是一份人教版（2024）七年级下册（2024）8.3 实数及其简单运算教学ppt课件，共34页。
1.理解无理数的概念，会判断一个数是否为无理数；(重点)2.进一步理解有理数和无理数的概念，会把实数进行分类；(重点)3.理解实数与数轴的关系，并进行相关运用；(难点)4.了解实数范围内的相反数、绝对值、倒数的意义；(重点)5.了解有理数的运算法则和运算律在实数范围内仍适用，能利用 化简对实数进行简单的四则运算.(难点)
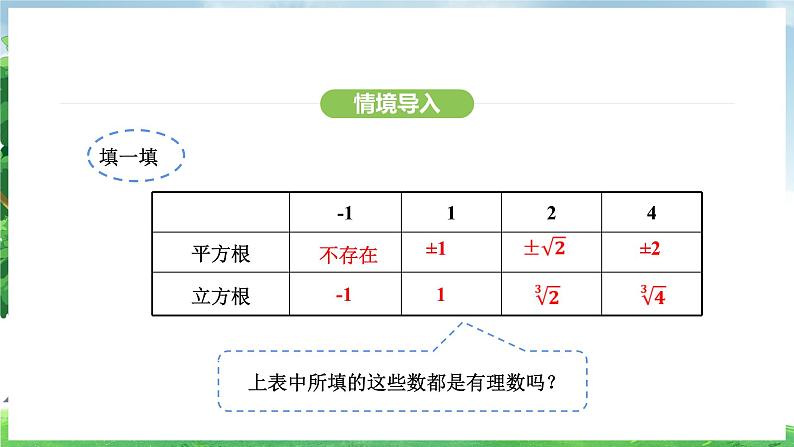
上表中所填的这些数都是有理数吗？
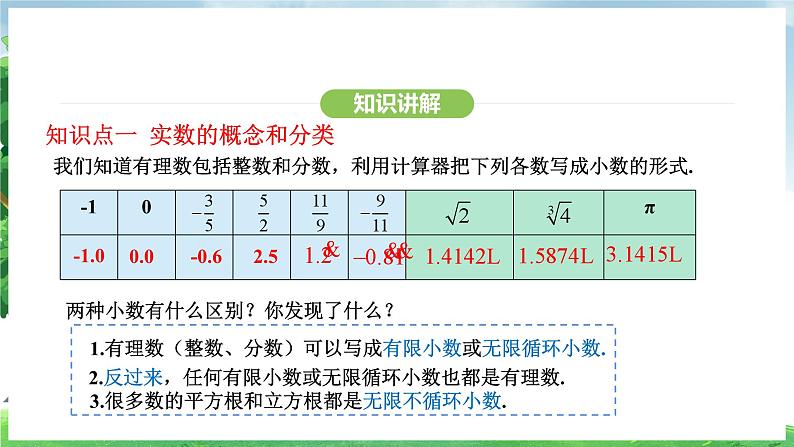
1.有理数（整数、分数）可以写成有限小数或无限循环小数.
2.反过来，任何有限小数或无限循环小数也都是有理数.
3.很多数的平方根和立方根都是无限不循环小数.
两种小数有什么区别？你发现了什么？
知识点一 实数的概念和分类
我们知道有理数包括整数和分数，利用计算器把下列各数写成小数的形式.
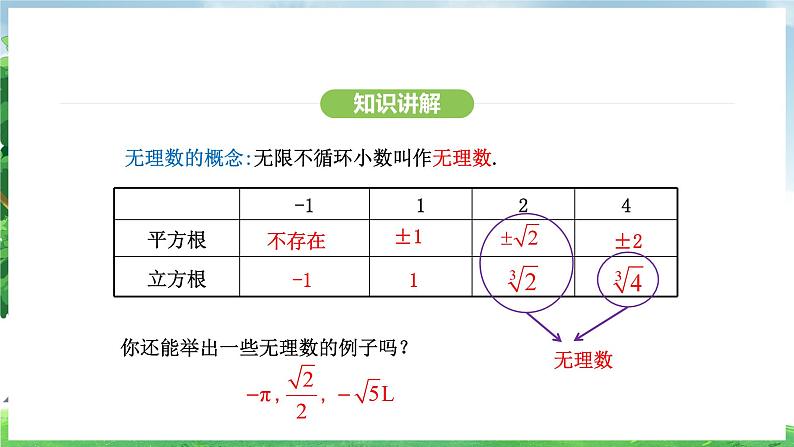
无理数的概念:无限不循环小数叫作无理数.
你还能举出一些无理数的例子吗？
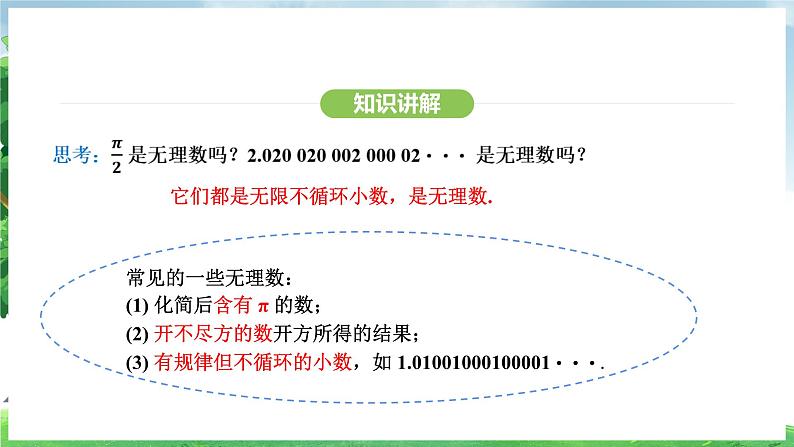
常见的一些无理数：(1) 化简后含有 π 的数；(2) 开不尽方的数开方所得的结果；(3) 有规律但不循环的小数，如 1.01001000100001···.
它们都是无限不循环小数，是无理数.
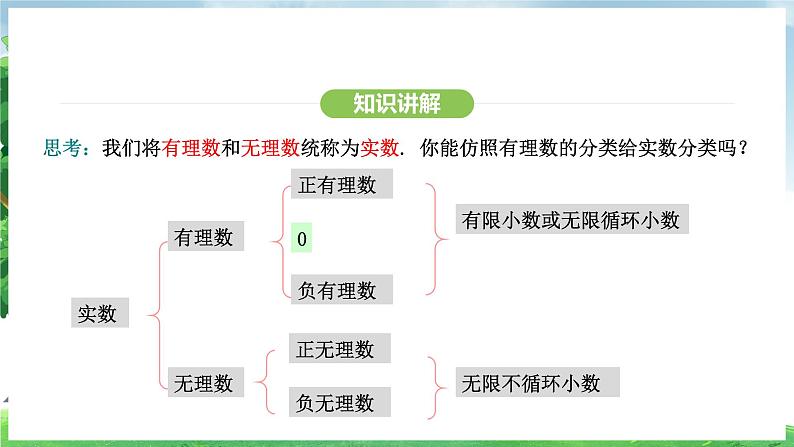
思考：我们将有理数和无理数统称为实数. 你能仿照有理数的分类给实数分类吗？
由于非零有理数和无理数都有正负之分，那么你能类比有理数的分类方法，按大小对实数分类吗？
例1.将下列各数分别填入相应的括号内：
例2.下列说法中，正确的是（ ）. A. 实数分为正实数和负实数 B. 无限小数都是无理数 C. 无理数都是无限小数 D. 带根号的数都是无理数
例3.有一个数值转换器，原理如图所示，当输入的 x 为 81 时，输出的 y 是（ ）.
探究：每个有理数都可以用数轴上的点来表示，无理数是否也能用数轴上的点表示出来呢？
知识点二 实数与数轴上的点
能不能在数轴上找到表示 π 的点呢？
每一个实数都可以用数轴上的一个点来表示；
反过来，数轴上的每一点都表示一个实数.
实数和数轴上的点是一一对应的.
与有理数一样，实数也可以比较大小：数轴上右边的点表示的实数比左边的点表示的实数大.
与有理数一样，在实数范围内：
例2.在数轴上表示下列各点，比较它们的大小，并用“ < ”连接它们.
有理数中的几个重要概念:
思考：无理数也有相反数吗？怎么表示？有绝对值吗？怎么表示？ 有倒数吗？怎么表示？
知识点三 实数的性质
在实数范围内 ，相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样．
实数 a 的相反数是 - a.实数 a 与 - a 表示的点到原点的距离相等.
总结：①一个正实数的绝对值是它本身；②一个负实数的绝对值是它的相反数；③ 0 的绝对值是 0.
例1.分别求下列各数的相反数、倒数和绝对值：
思考：有理数的运算律和运算性质在实数范围内仍然成立吗？
有理数的运算法则及运算性质在实数范围内同样适用.
填空：设 a，b，c 是任意实数，则
（1）a + b = （加法交换律）；
（2）(a + b) + c = （加法结合律）；
（3）a + 0 = 0 + a = ；
（4）a + (- a) = (- a) + a = ；
（5）ab = （乘法交换律）；
（6）(ab)c = （乘法结合律）；
a + (b + c)
（7） 1 · a = a · 1 = ；
（8）a(b + c) = （乘法对于加法的分配律）， (b + c)a = （乘法对于加法的分配律）；
（9）实数的减法运算规定为 a - b = a + ；
（10）对于每一个非零实数 a，存在一个实数 b，满足 a · b = b · a = 1， 我们把 b 叫作 a 的＿＿＿；
（11）实数的除法运算（除数 b≠0），规定为 a÷b = a · ；
（12）实数有一条重要性质：如果 a≠0，b≠0，那么 ab＿＿0.
1.每个正实数有且只有两个平方根，它们互为相反数. 0 的平方根是 0.在实数范围内，负数没有平方根.
2.在实数范围内，每个实数有且只有一个立方根， 而且与它本身的符号相同.
实数的平方根与立方根的性质：
此外，前面所学的有关数、式、方程（组）的性质、法则和解法，对于 实数仍然成立.
例1.计算下列各式的值：
当 m = 3 时，原式 = 0 + 1 + (3 - 1)2 = 1 + 4 = 5；当 m = -3 时，原式 = 0 + 1 + (-3 - 1)2 = 1 + 16 = 17.
解析：由已知得 a + b = 0，cd = 1，m = ±3.
5.观察下图，每个小正方形的边长均为 1.(1) 图中阴影部分(正方形)的面积是多少？他的边长是多少？(2) 阴影部分(正方形)的边长在哪两个整数之间？
解析：当 l = 0.5 时，
答：小重物来回摆动一次所用的时间是 1.4 s