人教版（2024）七年级下册（2024）10.2.1 代入消元法示范课ppt课件

这是一份人教版（2024）七年级下册（2024）10.2.1 代入消元法示范课ppt课件，共24页。PPT课件主要包含了随堂练习，课堂小结，∠1∠2，10-x，等量关系，根据题意可列方程组，x2y，x20000，所以这个方程组的解是，求出方程组的解等内容，欢迎下载使用。
1.理解并掌握代入消元法的意义；(重点)2.会用代入法解二元一次方程组.(难点)
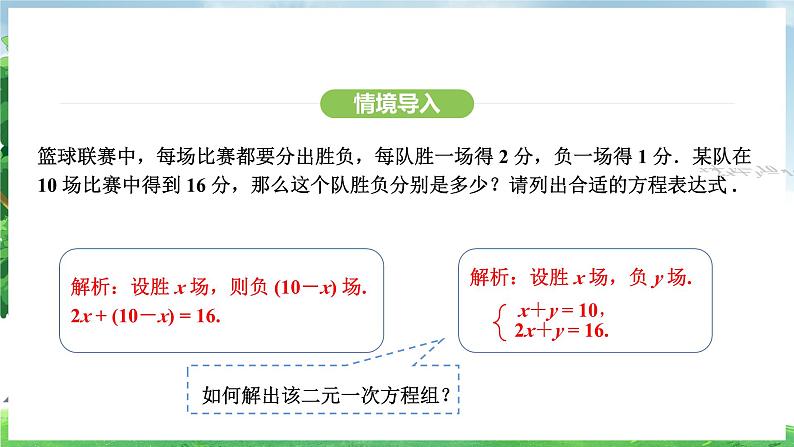
篮球联赛中，每场比赛都要分出胜负，每队胜一场得 2 分，负一场得 1 分．某队在 10 场比赛中得到 16 分，那么这个队胜负分别是多少？请列出合适的方程表达式 .
解析：设胜 x 场，负 y 场.
解析：设胜 x 场，则负 (10－x) 场.2x + (10－x) = 16.
如何解出该二元一次方程组？
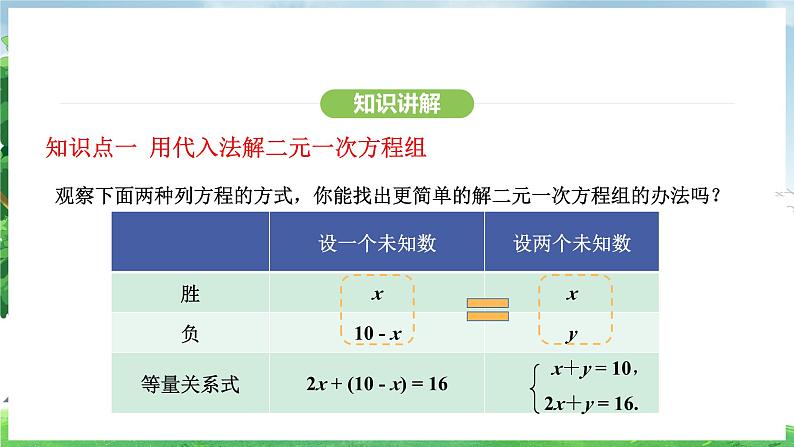
知识点一 用代入法解二元一次方程组
观察下面两种列方程的方式，你能找出更简单的解二元一次方程组的办法吗？
2x + y = 16
y = 10 - x ，
2x + (10 - x) = 16
总结：将未知数的个数由多化少，逐一解决的思想，叫作消元思想.
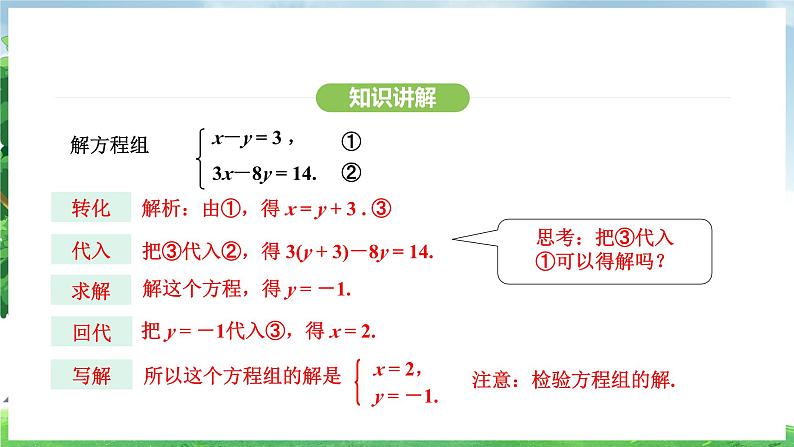
x－y = 3 ， 3x－8y = 14.
把 y = －1代入③，得 x = 2.
把③代入②，得 3(y + 3)－8y = 14.
解析：由①，得 x = y + 3 . ③
注意：检验方程组的解.
解方程组
解这个方程，得 y = －1.
思考：把③代入①可以得解吗？
解二元一次方程组的基本思路：“消元”
把二元一次方程组中一个方程的一个未知数用含有另一个未知数的式子表示出来，再代入另一个方程，实现消元，进而求得这个二元一次方程组的解，这种解方程的方法称为代入消元法，简称代入法.
x + 3y = 8， ①5x + 3y = 16. ②
例1. 解二元一次方程组：
用代入法解二元一次方程组时 ，挑选系数简单的方程变形 .当方程组中含有用一个未知数表示另一个未知数的关系式时，直接代入； 当方程组中有未知数的系数为 1 或 -1 时 ，选择系数为 1或-1 的方程进行变形； 当未知数的系数都不是 1 或 -1 时 ，一 般选择未知数系数的绝对值较小的方程变形.
代入法求二元一次方程组的技巧：
例1.根据市场调查，某种消毒液的大瓶装 (500 g) 和小瓶装 (250 g) 两种产品的销售数量 (按瓶计算) 比为 2∶5.某厂每天生产这种消毒液 22.5 t，这些消毒液应该分装大、小瓶两种产品各多少瓶？
(1) 大瓶数：小瓶数 = 2：5；
(2) 大瓶所装消毒液+小瓶所装消毒液 = 总生产量.
知识点二 用代入法解二元一次方程组的实际应用
设这些消毒液应该分装大瓶 x 瓶、小瓶 y 瓶.
请用代入消元法解此方程组.
5x = 2y， ①500x + 250y = 22 500 000. ②
500x + 250y = 22500000
代入消元法解二元一次方程组的一般步骤：
例2. 篮球联赛中，每场比赛都要分出胜负，胜一场得 2 分，负一场得 1 分，某队为了争取较好的名次，想在全部 20 场比赛中得到 35 分，那么这个队胜负场数分别是多少？
(1) 胜球场数 + 负球场数 = 全部场数；
(2) 胜球得分 + 负球得分 = 总得分.
解析： 设胜的场数是 x，负的场数是 y，可列方程组： 由①得 y＝20 - x . ③将③代入②，得 2x + 20 - x = 35 ，解得 x = 15.将 x = 15 代入③得 y = 5. 则这个方程组的解是答：这个队胜 15 场，负 5 场.
x+ y = 20， ①2x + y = 35. ②
x = 15， y = 5.
解析 ：(1)把 ①代入②,得 2x-3(3x+1)=4. 解这个方程，得 x = -1.把 x= -1代入①,得 y = -2.所以这个方程组的解是
y = 3x+1，　①　2x -3y = 4； ② 　
2x = y - 5， ①4x + 3y = 65. ②
1.用代入消元法解下列方程组.
y = 3x+1，　①　2x -3y = 4； ②
2x = y - 5， ①4x + 3y = 65. ②
2. 把下列方程分别用含 x 的式子表示 y，含 y 的式子表示 x： (1) 2x－y＝3；　　　　(2) 3x＋2y ＝1.
3.已知关于 x, y 的方程组 的解满足方程 x+y =8,求m的值.
先消去m,得到关于 x, y的方程
与 x+y=8组成 二元 一 次 方程组
3.已知关于 x, y 的方程组 的解满足方程 x+y=8,求m的值.
解析 ：把 ②代入①,得 3x+5y = 2x+3y+2.化简，得 x+2y = 2. ③把③与x+y=8联立组成方程组，得
把 代入②，得 2×14+3×（-6）= m，所以m= 10.
由②,得 b=3a-5.③把③代入①, 得 a+2( 3a-5）+3=0
5.李大叔去年承包了 10 亩地种植甲、乙两种蔬菜，共获利 18000 元，其中甲种蔬菜每亩获利 2000 元，乙种蔬菜每亩获利 1500 元，李大叔去年甲、乙两种蔬菜各种植了多少亩？
解析: 设甲、乙两种蔬菜各种植了 x、y 亩，依题意得 x + y = 10 ， ① 2000x + 1500y = 18000. ②由①得 y = 10 - x . ③将③代入②，得 2000x + 1500(10 - x) = 18000 ，解得 x = 6. 将 x = 6 代入③，得 y = 4. 答：李大叔去年甲、乙两种蔬菜各种植了 6 亩、4 亩.