清丰县仙庄镇初级中学2023-2024学年八年级上学期1月期末考试数学试卷(含答案)

这是一份清丰县仙庄镇初级中学2023-2024学年八年级上学期1月期末考试数学试卷(含答案)，共11页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（每小题3 分，共30分）
1. 下列式子是分式的是（ ）
A. xB. C. D.
答案：C
2. 夷人多封锁，国人当自强．国内某大学开设了芯片研究学院，研发某种芯片的厚度约为米，其中“”用科学记数法可表示为（ ）
A. B. C. D.
答案：B
3. 计算 的结果是（ ）
A. B. C. D.
答案：D
4. 下列等式分别是四位同学解方程过程中去分母的一步，其中正确的是（ ）
A. B. C. D.
答案：D
5. 如图，为了测量B点到河对面目标A之间的距离，在B点同侧选择一点C，测得，，然后在M处立了标杆，使，，此时测得的长就是A，B两点间的距离，那么判定的理由是（ ）
A. B. C. D.
答案：A
6. 多项式中各项公因式是（ ）
A. B. C. D.
答案：A
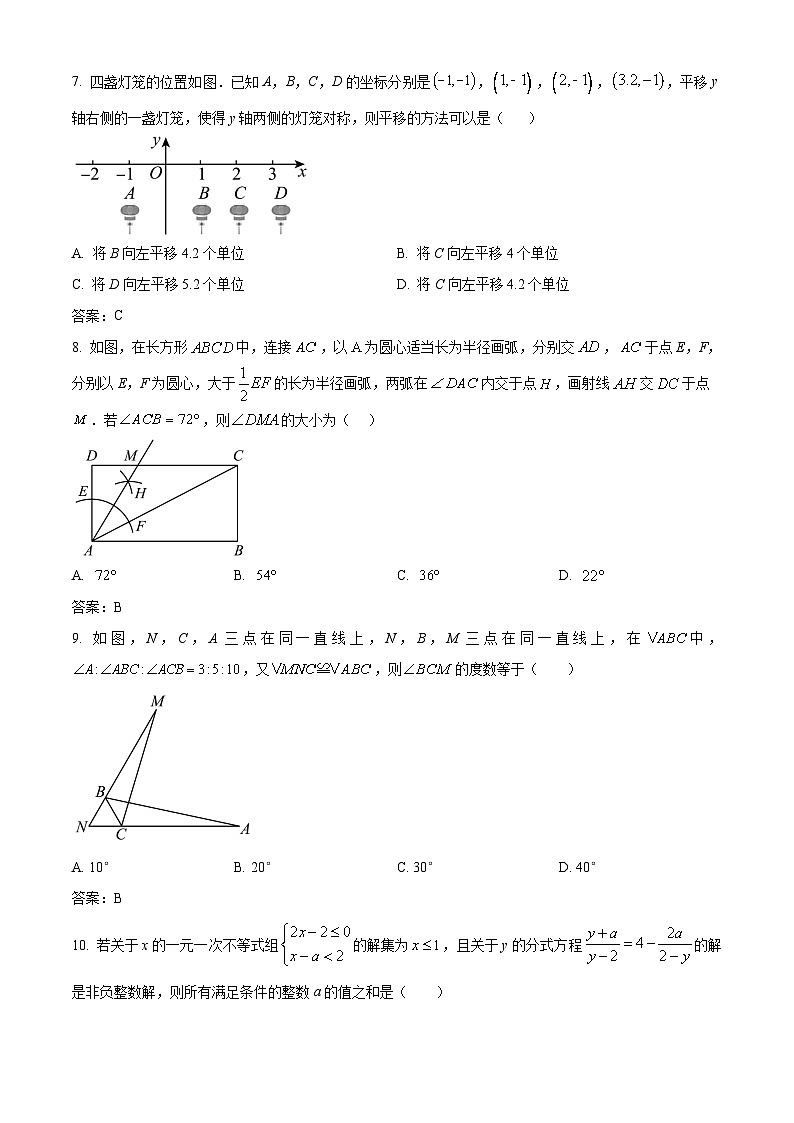
7. 四盏灯笼的位置如图．已知A，B，C，D的坐标分别是，，，，平移y轴右侧的一盏灯笼，使得y轴两侧的灯笼对称，则平移的方法可以是（ ）
A. 将B向左平移4.2个单位B. 将C向左平移4个单位
C. 将D向左平移5.2个单位D. 将C向左平移4.2个单位
答案：C
8. 如图，在长方形中，连接，以为圆心适当长为半径画弧，分别交，于点E，F，分别以E，F为圆心，大于的长为半径画弧，两弧在内交于点，画射线交于点．若，则的大小为（ ）

A. B. C. D.
答案：B
9. 如图，N，C，A三点在同一直线上，N，B，M三点在同一直线上，在中，，又，则的度数等于（ ）

A. 10°B. 20°C. 30°D. 40°
答案：B
10. 若关于x的一元一次不等式组的解集为，且关于y的分式方程的解是非负整数解，则所有满足条件的整数a的值之和是（ ）
A. B. C. D.
答案：B
二、填空题（每小题3 分，共15 分）
11. 要使分式有意义，则应满足的条件是___．
答案：x≠1
12. 如图：、相交于点O，，请你再补充一个条件，使，你补充的条件是______．
答案：或
13. 若是x的完全平方式，则____________________
答案：9
14. 如图，在中，，，于点D，于点M，与交于点P，则______．
答案：##110度
15. 如图，已知中，，点D为的中点．如果点P在线段上以的速度由B点向C点运动，同时点Q在线段上由C点向A点运动．当点Q的速度是 _____时，与全等．

答案：或2
三、解答题（共8题，共75 分）
16. （1）计算：；
（2）计算：；
（3）分解因式：；
（4）分解因式：
答案：（1）；
（2）；
（3）；
（4）
解∶（1）；
（2）；
（3） ；
（4）；
17. 解分式方程
（1）
（2）
答案：（1）；（2）
解：（1）去分母得：2x+4=3x，
解得：x=4，
经检验x=4是分式方程的解；
（2）去分母得：x（x+2）-1=（x+2）（x-2），
解得：，
经检验是分式方程的解．
【点睛】本题考查解分式方程，解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解．解分式方程一定注意要验根．
18. 先化简，再求值：
（1），其中，
（2），其中
答案：（1）；
（2）；
【小问1详解】
，
当，时，
原式．
【小问2详解】
，
当时，
原式．
19. 如图，已知，点B在线段上．求的度数．
答案：
解：∵，
∴，即，
在和中，
，
∴，
∴，
∴，
∵，
∴．
20. 如图，已知△ABC中，点D在边AC上，且BC=CD
(1)用尺规作出∠ACB的平分线CP(保留作图痕迹，不要求写作法)；
(2)在（1）中，设CP与AB相交于点E ,连接DE求证：BE =DE
答案：（1）作图见解析（2）证明见解析
(1)射线CP为所求
（2）证明：
∵CP是∠ACB的平分线
∴∠DCE=∠BCE
∵BC=CD，CE=CE
∴△DCE≌△BCE
∴BE =DE
21. 某水果超市在批发市场购买某种水果销售，第一次用1200元购进若干千克，并以每千克8元出售，很快售完，由于水果畅销，第二次购买时，每千克的进价比第一次提高了，用1452元所购买的质量比第一次多20千克，以每千克9元售出100千克后，因出现高温天气，水果不易保鲜，为减少损失，便降价售完剩余的水果．设第一次购进的水果的进价是x元/千克．
（1）第二次购进水果的进价是______元/千克，第一次、第二次购进水果的质量分别为______千克和______千克，（用含有x的式子表示）；
（2）求第一次购买的水果的进价是每千克多少元？
（3）该果品店在这两次销售中，总体上是盈利还是亏损？盈利或亏损了多少元？
答案：（1）1.1x，，
（2）6元 （3）总体上是盈利了，盈利了388元
【小问1详解】
第二次购进水果的进价是元/千克，第一次、第二次购进水果的质量分别为千克和千克，
故答案为：1.1x，，
【小问2详解】
根据题意得，
解得．
检验：当时，
是原方程的解且符合题意．
答：第一次购买水果的进价是每千克6元．
【小问3详解】
第一次购买水果（千克）．第二次购买水果（千克）．
第一次利润为（元），
第二次利润为（元）．
所以两次共盈利（元）．
所以该果品店在这两次销售中，总体上是盈利了，盈利了388元．
22. 阅读理解：
解决问题：
（1）若，求x、y的值；
（2）已知a，b，c是的三边长且满足，
①直接写出______，______；
②若c是中最短边的边长（即；），且c为整数，求出c的值．
答案：（1），
（2） ①. 3 ②. 4；②2
【小问1详解】
解： ，
，
，
，，
解得，；
【小问2详解】
解：①，
，
，
解得，，
故答案为：3，4；
②，，
，
又是中最短边的边长，
，
为整数，
为2．
23. 如图，在平面直角坐标系中，等边三角形ABC的BC边在轴上，顶点A在y轴的正半轴上，OB=a，，△ABC的面积为36.
（1）求点的坐标；
（2）动点从点出发，以每秒1个单位的速度沿的方向运动．设运动时间为，求为何值时，过两点的直线将的周长分成两个部分，使其中一部分是另一部分的2倍；
（3）设点为的中点，连接，在x轴上是否存在点，使是以为腰的等腰三角形？如果存在，请求出点的坐标；如果不存在，请说明理由．
答案：（1）A(0，)，（2）t=6或t=18，（3）在x轴上存在点Q，Q1(，0)， Q2(，0) ，Q3(-12，0)，使△DCQ是以CD为腰的等腰三角形．见解析.
解：（1）∵△ABC是等边三角形，AO⊥BC
∴ CO=BO=a
∵S△ABC=BC·OA=×2a×=
∵a＞0
∴a=6
∴OA=
∴A(0，)
（2）∵CO=BO=6
∴AB=AC=BC=12
①当P在AB上时（如图①），
BP=t，AP=AB-BP=12-t
∵OP分△ABC周长为1:2
∴(BP+BO):(AP+AC+OC)=1:2
∴(6+t):(12-t+12+6)=1:2
解得t=6
②当P在AC上时（如图②），
BA+AP=t，PC=24-t
则有（BO+BA+AP）:(PC+OC)=2:1
∴(6+t):(24-t+6)=2:1
解得t=18
∴t=6或t=18时，OP所在直线分△ABC周长为1:2.
（3）如图③∵点D为AB的中点，△ABC是等边三角形
∴ CD⊥AB ∠BCD=30°
∵S△ABC=BC·OA=AB·CD
∴ CD=OA=， BD=6
△DCQ是以CD为腰的等腰三角形，点Q在x轴上.分以下情况讨论：
① 当CQ=CD时，CQ=
∵OC=6 ，C(6，0)
∴ Q1(，0)Q2(，0)
②当DQ=DC时，∠DQB=∠DCQ=30°
又∵∠ABC=60°
∴∠QDB=∠ABC-∠DQC=60°-30°=30°
∴∠QDB=∠DQB
∴QB=BD=6
∴OQ=12
∴Q3(-12，0)
所以，在x轴上存在点Q，Q1(，0)， Q2(，0)，Q3(-12，0)使△DCQ是以CD为腰的等腰三角形．
例：已知：，
求：m和n的值．
解：∵，
∴，
∴，
∴，，
∴，．