清丰县仙庄镇初级中学2024届九年级上学期1月期末考试数学试卷(含答案)

这是一份清丰县仙庄镇初级中学2024届九年级上学期1月期末考试数学试卷(含答案)，共11页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题(每小题3 分，共30分)
1.若x=2 是关于x的 一元二次方程x²+mx-2=0 的一个根，则m的值为 【 】
2.若反比例函数y=kxk≠0 的图象经过点(2，-3)，则它的图象也一定经过的点是【 】
A.( -2, -3) B.( -3, -2) C.(1,-6) D.(6,1)
3.如图,将△OAB绕点O逆时针旋转80°,得到△OCD,若∠A=2∠D=100°,则∠α的度数是【 】
A.50° B.60° C.40° D.30°
4.如图,点A,B,C,D,E均在⊙O上,∠BAC=15°,∠CED=30°,则∠BOD的度数为 【 】
A.45° B.60° C.75° D.90°
5.如图，直线l₁∥l₂∥l₃,直线 AC 和 DF 被 l₁,l₂,l₃所截,AB=5,BC=6,EF=4,则DE的长为【 】
A.2 B.3 C.4 D. 103
6.在一个不透明的袋子中放有若干个球，其中有6个白球，其余是红球，这些球除颜色外完全相同.每次把球充分搅匀后，任意摸出一个球记下颜色再放回袋子.通过大量重复试验后，发现摸到白球的频率稳定在0.25 左右，则红球的个数约是【 】
A.2 B.12 C.18 D.24
7.对于y=3x-1²+2 的性质，下列叙述正确的是 【 】
A.顶点坐标为(-1,2) B.对称轴为直线 x=1
C.当x=1时,y有最大值2 D.当x≥1时,y随x增大而减小
8.在正比例函数y=kx(k≠0)中，y随x的增大而减小，则关于x的方程x²-x+k=0根的情况是【 】
A.有两个相等的实数根 B.有两个不相等的实数根
C.无实数根 D.无法确定
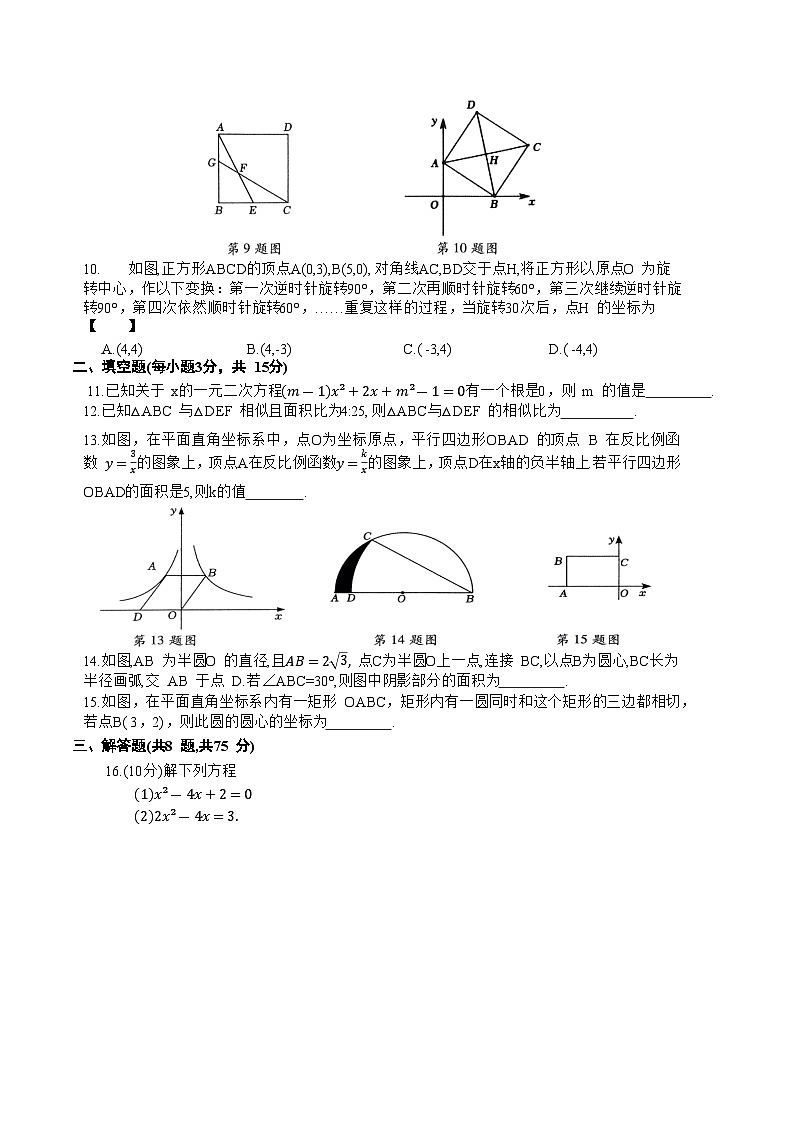
9.如图,已知正方形ABCD的边长为2,点E 是 BC的中点,连结AE,点F 在 AE上,且EF=CE,连结 CF 并延长交AB 于点 G.则 BG的长是【 】
A.5-1 B.5+1 C.3-5 D.1
如图,正方形ABCD的顶点A(0,3),B(5,0),对角线AC,BD交于点H,将正方形以原点O 为旋转中心，作以下变换：第一次逆时针旋转90°，第二次再顺时针旋转60°，第三次继续逆时针旋转90°，第四次依然顺时针旋转60°，……重复这样的过程，当旋转30次后，点H 的坐标为【 】
A.(4,4) B.(4,-3) C.( -3,4) D.( -4,4)
二、填空题(每小题3分，共 15分)
11.已知关于 x的一元二次方程m-1x²+2x+m²-1=0有一个根是0，则 m 的值是 .
12.已知△ABC 与△DEF 相似且面积比为4:25,则△ABC与△DEF 的相似比为 .
13.如图，在平面直角坐标系中，点O为坐标原点，平行四边形OBAD 的顶点 B 在反比例函数 y=3x的图象上，顶点A在反比例函数y=kx的图象上，顶点D在x轴的负半轴上.若平行四边形 OBAD的面积是5,则k的值 .
14.如图,AB 为半圆O 的直径,且AB=23, 点C为半圆O上一点,连接 BC,以点B为圆心,BC长为半径画弧,交 AB 于点 D.若∠ABC=30°,则图中阴影部分的面积为 .
15.如图，在平面直角坐标系内有一矩形 OABC，矩形内有一圆同时和这个矩形的三边都相切，若点B( 3，2)，则此圆的圆心的坐标为 .
三、解答题(共8 题,共75 分)
16.(10分)解下列方程
1x²-4x+2=0
22x²-4x=3.
17.(9分)如图,在 △ABP中,C,D分别是AP,BP上的点.若CD=CP=4,DP=5,AC=3.5,
BD=1
(1)求证:△ABP~△DCP;
(2)求 AB 的长.
18.(9分)将正面分别标有数字1，2，3，6，背面花色相同的四张卡片洗匀后，背面朝上放在桌面上，先从中随机抽取一张，再从剩下的三张中随机抽取第二张.
(1)求两次抽取的卡片上的数字之和大于5的概率；
(2)求两次抽取的卡片上的数字之和为奇数的概率.
19.(9分)如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A-32,B-13; C-11,请按如下要求画图：
(1)以坐标原点 O 为旋转中心，将△ABC顺时针旋转90°,得到△A₁B₁C₁,请画出 △A₁B₁C₁，并写出点 B 的对应点B₁的坐标；
(2)以坐标原点 O 为位似中心，在 x 轴下方，画出△ABC的位似图形△A₂B₂C₂,，使它与△ABC的位似比为2：1.并写出点 B 的对应点B₂的坐标.
3△ABC内部一点M 的 坐标为(a,b),写出M 在△A₂B₂C₂中的对应点M₂的坐标.
20.(9分)如图,在△ABC中,∠C=90°,点D 是 AB 边上一点,以BD为直径的⊙O与边 AC 相切于点 E，与边 BC交于点F，过点 E作EH⊥AB于点 H,连接 BE.
(1)求证: BC=BH;
(2)若AB=5,AC=4,求 CE 的长.
B
21.(9分)如图,一次函数 y₁=mx+nm≠0的图象与反比例函数y2=kxk≠0的图象交于 A(a,-1),B(-1,3)两点，且一次函数 y₁的图象交x轴于点C，交y轴于点 D.
(1)求一次函数和反比例函数的解析式；
(2)在第四象限的一次函数图象上有 一点P，满足CP=6BD,，请求出点 P 的坐标；
(3)当y₁≤y₂时，直接写出x的取值范围.
22.(10分)如图,抛物线y=x²+bx+c 交x轴于 C，D两点，交y轴于点 E，其中点 C 的坐标为-10,对称轴为x=1..点A，B为坐标平面内两点，其坐标为 A12-5,B4-5
(1)求抛物线的解析式及顶点坐标；
(2)当-1≤x≤2时，求y的取值范围；
(3)连接AB,若抛物线y=x²+bx+c 向下平移kk0)个单位时，与线段 AB 只有一个共点，结合函数图象，直接写出k的取值范围.
23.(10分)如图,两个等腰直角.△ABC和 △CDE中,∠ACB=∠DCE=90°.
(1)观察猜想如图1，点E 在 BC上，线段 AE 与 BD 的数量关系是 ，位置关系是 .
(2)探究证明：把△CDE绕直角顶点 C 旋转到图2的位置，(1)中的结论还成立吗? 说明理由；
(3)拓展延伸：把△CDE绕点 C 在平面内自由旋转，若AC=BC=13,DE=10,当A、E、D 三点在直线上时，请直接写出AD的长.
2023–2024 学年度第一学期期末测试卷)参考答案
九年级数学(RJ)
一、选择题(每小题3分，共30分)
1. A 2. C 3. A 4. D 5. D 6. C 7. B 8. B 9. A 10. D
二、填空题(每小题3分，共15分)
11. -1 12.2:5 13. -2 14.334-π4 15.(-2,1)或( -1,1)
三、解答题(共8题，共75分)
16.解: 1x²-4x+2²=-2+2²,
即 x-2²=2
x-2=±2,
x1=2+2,x2=2-2;………………………………………………………………5分
22x²-4x=3,
x2-2x=32,
x2-2x+12=32+12,
x-12=52,
x1=2+102,x2=2-102. ………………………………………………………………5分
17.解:(1)证明:∵CD=CP=4,DP=5,AC=3.5,BD=1,
∴AP=AC+CP=3.5+4=7.5,BP=BD+DP=1+5=6,
∴PDPC=54,7.56=54,
∴PDPC=APBP,
∵ ∠DPC=∠APB,
∴△ABP∽△DCP;………………………………………………………………5分
(2)∵△ABP∽△DCP,
∴ABBP=CDCP
即: AB6=44,
∴AB=6……………………………………………………………………9分
18.解:(1)画树状图如下:
共有 12种等可能的结果，其中两次抽取的卡片上的数字之和大于5的结果有6种，
∴两次抽取的卡片上的数字之和大于5 的概率为 612=12;………………………5分
(2)由(1)可知，共有12种等可能的结果，其中两次抽取的卡片上的数字之和为奇数的结果有8种，∴两次抽取的卡片上的数字之和为奇数的概率为 812=23.……………9分
19.解:(1)如图, △A₁B₁C₁即为所求，其中点B 的对应点 B₁₁的坐标为(3,1).……4分
(2)如图所示, △A₂B₂C₂即为所求，点B 的 对应点B ₂ 的坐标为( 2-6;………8分
(3)M在 △A₂B₂C₂中的对应点M₂的坐标(-2a,-2b).…………………………………9分
20.(1)证明:连接OE,如图,
∵AC为切线,∴ OE⊥AC,∴ ∠AEO=90°,
∵∠C=90°,∴OE∥BC,∴∠1=∠3,
∵OB=OE,∴∠2=∠3,∴∠1=∠2,
∵ EH=EC,
在 Rt△BEH 和 Rt△BEC 中
∴Rt△BEH≌Rt△BEC(HL),∴BC=BH;………………………………………………5分
(2)在 Rt△ABC 中, BC=52-42=3,
设OE=r,则OA=5-r,
∵OE∥BC,∴ △AOE∽△ABC,
∴AOAB=OEBC,即 5-r5=r3,解得 r=158,∴AO=5-r=258,
在 Rt△AOE 中, AE=2582-1582=52,
∴CE=AC-AE=4-52=32.……………………………………………………9分
21.解: 1∵y2=kx比例函数的图象过点 B( -1,3),
∴k=-1×3=-3,∴y2=-3x,…………………………………………………2分
∵A(a,-1)在双曲线上, ∴-1=-3a,∴a=3,∴A3-1,…………………………………3分
∵一次函数 y₁=mx+nm≠0)的图象经过A、B两点，
∴一次函数的解析式 y₁=-x+2;……………………………………………5分
(2)在y=-x+2中,当x=0时,y=2;当y=0时,则x=2,∴D(0,2),C(2,0),
∵B(-1,3),∴BD= 2,
∵CP=6BD,∴CP=6 2,
设点 P 的坐标为(x,-x+2),则 CP=x-22+-x+22=62,
解得 x=8或-4(舍去),
将x=8代入 y₁=-x+2,,得y= -6,
∴P的坐标为(8,-6);……………………………………………………………8分
(3)观察图象可知，当 y₁≤y₂时,x的取值范围是-1≤x2-1,
∴x= -1时,y=0为最大值,
∴当-1≤x≤2时,-4≤y≤0…………………………………………………………8分
(3)k=1或 54