新高考数学一轮复习精品讲练测第1章专题01 集合（2份，原卷版+解析版）

这是一份新高考数学一轮复习精品讲练测第1章专题01 集合（2份，原卷版+解析版），文件包含新高考数学一轮复习精品讲练测第1章专题01集合教师版doc、新高考数学一轮复习精品讲练测第1章专题01集合学生版doc等2份试卷配套教学资源，其中试卷共38页， 欢迎下载使用。
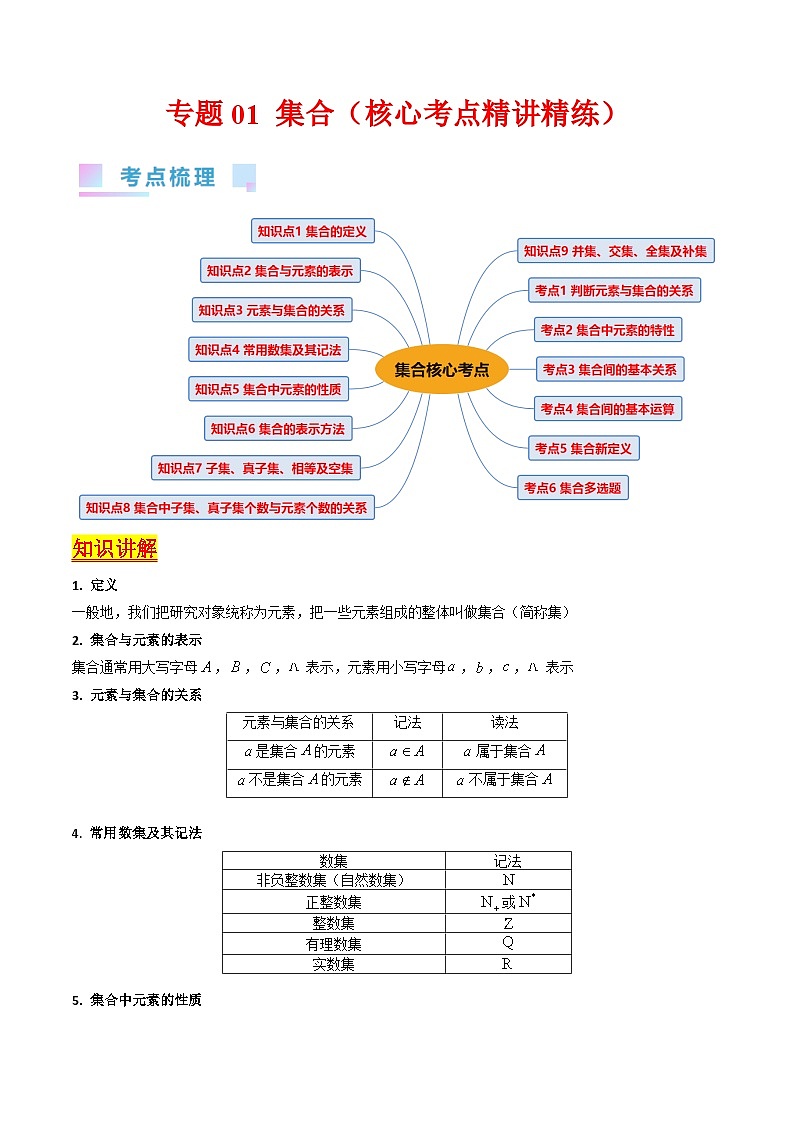
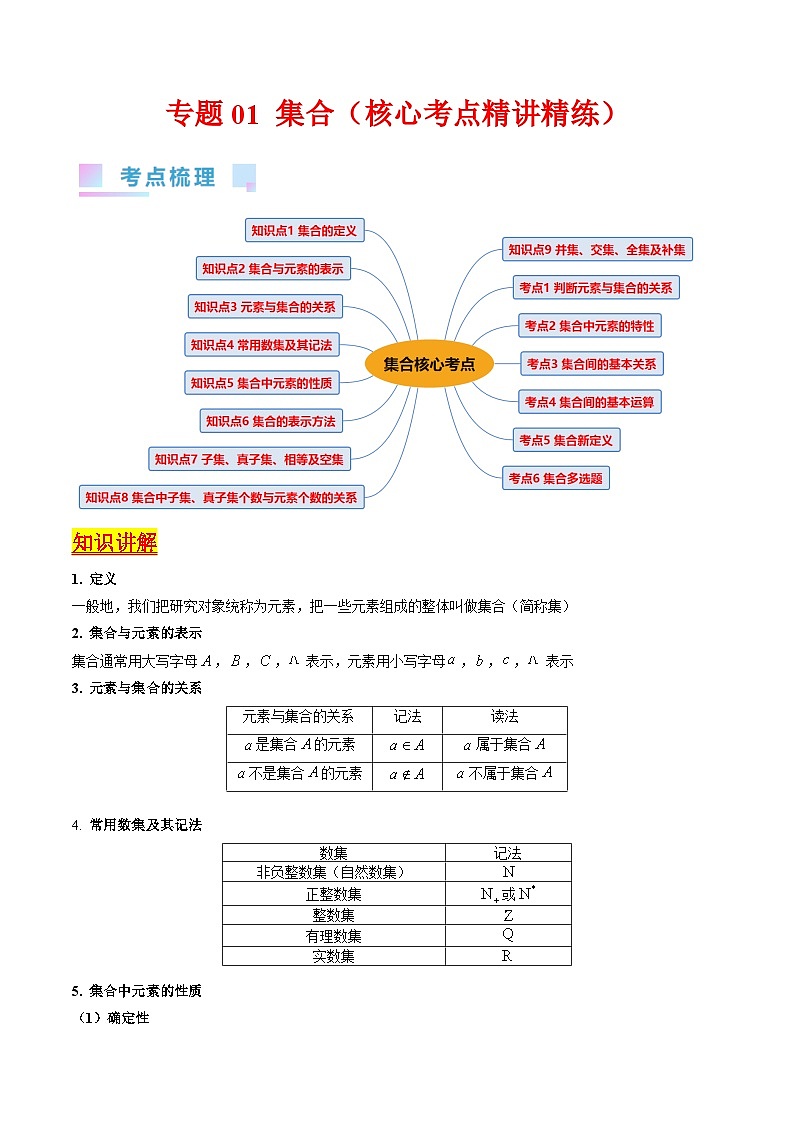
知识讲解
定义
一般地，我们把研究对象统称为元素，把一些元素组成的整体叫做集合（简称集）
集合与元素的表示
集合通常用大写字母，，，表示，元素用小写字母，，，表示
元素与集合的关系
常用数集及其记法
集合中元素的性质
确定性
给定的集合，它的元素必须是确定的；
也就是说，给定一个集合，那么任何元素在不在这个集合中就确定了。
互异性
一个给定集合中的元素是互不相同的；
也就是说，集合中的元素是不能重复出现的。
无序性
组成集合的元素没有顺序之分，只要构成两个集合的元素是一样的，我们就称这两个集合是相等的。
集合的表示方法
列举法
我们可以把“地球上的四大洋"组成的集合表示为
把“方程的所有实数根”组成的集合表示为.
像这样把集合的元素一一列举出来.并用花括号“”括起来表示集合的方法叫做列举法.
描述法
用集合所含元素的共同特征表示集合的方法叫做描述法
具体方法是在花括号内先写上表示这个集合元素的一般符号及取值（或变化）范围，再画一条竖线，在竖线后写上这个元素所具有的共同特征。
数学表达式为：，其中为代表元素，为共同特征。
子集
一般地,对于两个集合A、B,如果集合A中任意一个元素都是集合B中的元素,我们就说这两个集合有包含关系,称集合A为集合B的子集，
记作.读作“A含于B”(或“B包含A”).
真子集
如果集合,但存在元素,我们称集合A是集合B的真子集，记作或，读作“真含于或（真包含）”
集合相等
如果集合A是集合B的子集,且集合B是集合A的子集,
此时,集合A与集合B中的元素是一样的,因此,集合A与集合B相等,记作A=B.
空集
我们把不含任何元素的集合叫做空集,记为
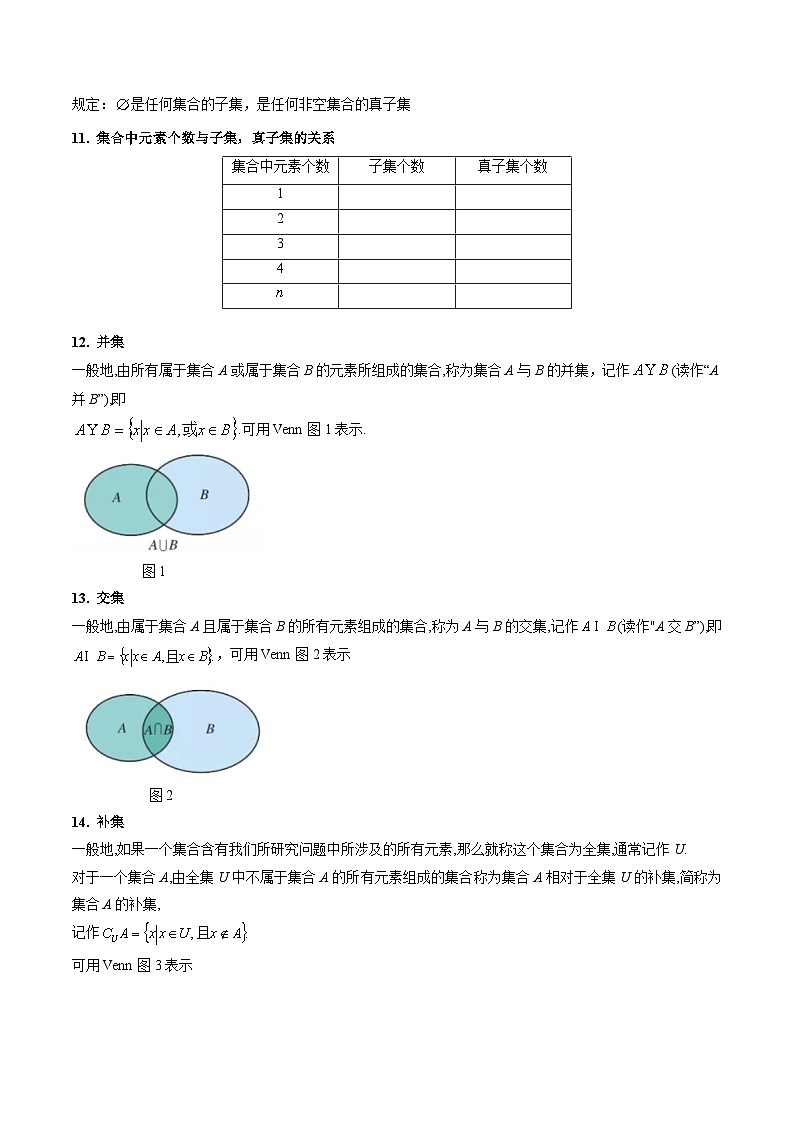
规定：是任何集合的子集，是任何非空集合的真子集
集合中元素个数与子集，真子集的关系
并集
一般地,由所有属于集合A或属于集合B的元素所组成的集合,称为集合A与B的并集，记作(读作“A并B”),即
.可用Venn图1表示.

图1
交集
一般地,由属于集合A且属于集合B的所有元素组成的集合,称为A与B的交集,记作(读作"A交B”),即
，可用Venn图2表示
图2
补集
一般地,如果一个集合含有我们所研究问题中所涉及的所有元素,那么就称这个集合为全集,通常记作U.
对于一个集合A,由全集U中不属于集合A的所有元素组成的集合称为集合A相对于全集U的补集,简称为集合A的补集,
记作
可用Venn图3表示
图3
并集的运算
交集的运算
补集的运算
德摩根定律
考点一、判断元素与集合的关系
1．（2023·河北秦皇岛·秦皇岛一中校考二模）设全集，若集合满足，则（ ）
A．B．C．D．
2．（2023·黑龙江牡丹江·牡丹江市第三高级中学校考三模）已知集合，且，则a可以为（ ）
A．－2B．－1C．D．
1．（2023·全国·高三专题练习）已知全集，则（ ）
A． B． C． D．
2．（2023·全国·校联考三模）已知全集，则（ ）
A．B．
C．D．
考点二、集合中元素的特性
1．（2023·全国·高三专题练习）若，则的可能取值有（ ）
A．0B．0，1C．0，3D．0，1，3
2．（2023·全国·高三专题练习）已知，，若集合，则的值为（ ）
A．B．C．D．
1．（2023·全国·高三专题练习）已知，若，则实数构成的集合的元素个数是（ ）
A．B．C．D．
2．（2023·全国·高三专题练习）集合，若，则（ ）
A．B．3或C．3D．3或或5
考点三、集合间的基本关系
1．（2023·新高考Ⅱ卷高考真题）设集合，，若，则（ ）．
A．2B．1C．D．
2．（2023·重庆·校联考三模）数集的非空真子集个数为（ ）
A．32B．31C．30D．29
3．（2023·江苏南京·统考二模）集合的子集个数为（ ）
A．2B．4C．8D．16
4．（2023·辽宁·辽宁实验中学校联考模拟预测）设集合，，若，则（ ）
A．0B．1C．2D．
1．（2023·湖南怀化·统考二模）已知集合，则的真子集共有（ ）
A．3个B．6个C．7个D．8个
2．（2023·辽宁大连·统考三模）已知集合，满足，则（ ）
A．B．C．D．
3．（2023·江苏·统考一模）设，，则（ ）
A．B．C．D．
考点四、集合的基本运算
1．（2023·新高考Ⅰ卷高考真题）已知集合，，则（ ）
A．B．C．D．2
2．（2022·新高考Ⅰ卷高考真题）若集合，则（ ）
A．B．C．D．
3．（2022·新高考Ⅱ卷高考真题）已知集合，则（ ）
A．B．C．D．
1．（2023·湖南·校联考二模）已知集合，则（ ）
A．B．C．D．
2．（2023·辽宁葫芦岛·统考二模）若集合，则＝（ ）
A．B．
C．D．
3．（2023·湖南常德·二模）已知全集，集合，，则（ ）
A．B．C．D．
4．（2023·河北唐山·统考二模）已知全集，集合，，则（ ）
A．B．
C．D．
5．（2023·山西临汾·统考二模）已知集合，则（ ）
A．B．
C．D．
6．（2023·河北秦皇岛·秦皇岛一中校考二模）设全集，若集合满足，则（ ）
A．B．C．D．
7．（2023·湖南邵阳·统考三模）已知集合，则（ ）
A．B．
C．或D．或
8．（2023·河北邯郸·统考三模）已知集合，，则（ ）
A．B．C．D．
9．（2023·浙江绍兴·统考模拟预测）若集合，，则（ ）
A．B．
C．D．
10．（2023·海南·统考模拟预测）已知全集，集合，，则Venn图中阴影部分表示的集合为（ ）．

A．B．C．D．
考点五、集合新定义
1．（2023·全国·高三专题练习）定义集合且.已知集合，，则中元素的个数为（ ）
A．6B．5C．4D．7
2．（2023·全国·高三专题练习）定义集合，设集合，，则中元素的个数为（ ）
A．B．C．D．
1．（2023·全国·高三专题练习）定义集合且，已知集合，则（ ）
A．B．C．D．
2．（2023·全国·高三专题练习）定义集合运算，若集合，则（ ）
A．B．C．D．
考点六、集合多选题
1．（2023·山东潍坊·统考一模）若非空集合满足：，则（ ）
A．B．
C．D．
2．（2023·全国·高三专题练习）已知集合A，B均为R的子集，若，则（ ）
A．B．
C．D．
1．（2023·全国·高三专题练习）已知、均为实数集的子集，且，则下列结论中正确的是（ ）
A．B．
C．D．
2．（2023·全国·高三专题练习）已知集合，，若使成立的实数a的取值集合为M，则M的一个真子集可以是（ ）
A．B．C．D．
【基础过关】
1．（2023·辽宁辽阳·统考二模）已知集合，则（ ）
A．B．C．D．
2．（2023·河北·校联考一模）已知集合，，则（ ）
A．B．C．D．
3．（2023·福建莆田·统考二模）设全集，，则（ ）
A．B．C．D．
4．（2023·山东威海·统考二模）已知全集，集合满足，则（ ）
A．B．C．D．
5．（2023·湖北武汉·统考二模）已知集合，，则（ ）
A．B．C．D．
6．（2023·湖南常德·二模）已知全集，集合，，则（ ）
A．B．C．D．
7．（2023·浙江·统考二模）已知集合，则（ ）
A．B．C．D．
8．（2023·广东广州·华南师大附中校考三模）已知集合，，则（ ）
A．B．C．D．
9．（2023·重庆·统考二模）已知集合，，则（ ）
A．B．C．D．
10．（2023·江苏南通·二模）若M，N是U的非空子集，，则（ ）
A． B． C． D．
【能力提升】
1．（2023·重庆·校联考三模）数集的非空真子集个数为（ ）
A．32B．31C．30D．29
2．（2023·湖南·校联考二模）已知集合，则（ ）
A．B．C．D．
3．（2023·福建漳州·统考三模）已知集合，，则（ ）
A．B．C．D．
4．（2023·山东烟台·统考三模）已知全集，集合，则（ ）
A．B．C．D．
5．（2023·湖北武汉·统考三模）设集合，，则（ ）
A．B．
C．D．
6．（2023·广东汕头·金山中学校考三模）已知集合，，则（ ）
A．B．
C．D．或
7．（2023·江苏盐城·校考三模）集合，，则（ ）
A．B．
C．D．
8．（2023·浙江·校联考三模）若集合，则（ ）
A．B．C．D．
9．（2023·辽宁沈阳·沈阳二中校考模拟预测）设集合，集合，则（ ）
A．B．C．D．
10．（2023·河北·校联考一模）已知集合，集合，则（ ）
A．B．C．D．
【真题感知】
1．（2021·新高考Ⅰ卷高考真题）设集合，，则（ ）
A．B．C．D．
2．（2021·新高考Ⅱ卷高考真题）设集合，则（ ）
A．B．C．D．
3．（2020·新高考Ⅰ卷高考真题）设集合A={x|1≤x≤3}，B={x|2