新高考数学一轮复习精品讲练测第5章第01讲 平面向量的概念 线性运算及坐标运算（2份，原卷版+解析版）

这是一份新高考数学一轮复习精品讲练测第5章第01讲 平面向量的概念 线性运算及坐标运算（2份，原卷版+解析版），文件包含新高考数学一轮复习精品讲练测第5章第01讲平面向量的概念线性运算及坐标运算教师版doc、新高考数学一轮复习精品讲练测第5章第01讲平面向量的概念线性运算及坐标运算学生版doc等2份试卷配套教学资源，其中试卷共29页， 欢迎下载使用。

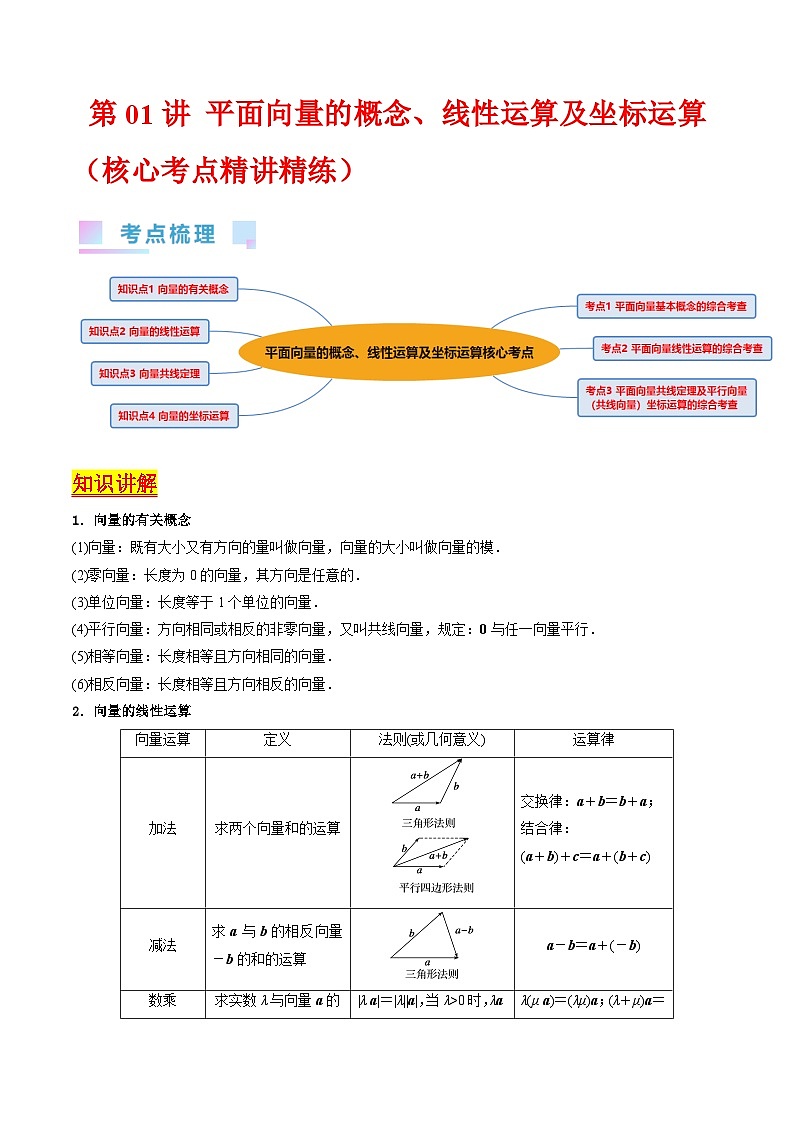
知识讲解
1．向量的有关概念
(1)向量：既有大小又有方向的量叫做向量，向量的大小叫做向量的模．
(2)零向量：长度为0的向量，其方向是任意的．
(3)单位向量：长度等于1个单位的向量．
(4)平行向量：方向相同或相反的非零向量，又叫共线向量，规定：0与任一向量平行．
(5)相等向量：长度相等且方向相同的向量．
(6)相反向量：长度相等且方向相反的向量．
2．向量的线性运算
1．平面向量加减法求解的关键是：对平面向量加法抓住“共起点”或“首尾相连”．对平面向量减法应抓住“共起点，连两终点，指向被减向量的终点”，再观察图形对向量进行等价转化，即可快速得到结果．
2．在一般向量的线性运算中，只要把其中的向量当作一个字母看待即可，其运算方法类似于代数中合并同类项的运算，在计算时可以进行类比．
3.向量共线定理
向量b与非零向量a共线的充要条件是有且只有一个实数λ，使得b＝λa.
向量共线定理可以解决一些向量共线，点共线问题，也可由共线求参数；对于线段的定比分点问题，用向量共线定理求解则更加简洁．
（1）若eq \(OA,\s\up6(→))＝λeq \(OB,\s\up6(→))＋μeq \(OC,\s\up6(→))(λ，μ为常数)，则A，B，C三点共线的充要条件是λ＋μ＝1.
（2）P为线段AB的中点⇔eq \(OP,\s\up15(→))＝eq \f(1,2)(eq \(OA,\s\up15(→))＋eq \(OB,\s\up15(→)))．
4.向量的坐标运算
两点间的向量坐标公式：
，，终点坐标始点坐标
向量的加减法
，，
向量的数乘运算
，则：
向量的模
，则的模
相反向量
已知，则；已知
单位向量
向量的平行关系
，，
考点一、平面向量基本概念的综合考查
1．（辽宁·高考真题）已知点则与同方向的单位向量为
A．B．C．D．
2．（福建·高考真题）对于向量和实数，下列命题中真命题是( )
A．若，则或B．若，则或
C．若，则或D．若，则
1．（2023·江苏南京·南京市秦淮中学校考模拟预测）下列说法中正确的是（ ）
A．单位向量都相等
B．平行向量不一定是共线向量
C．对于任意向量，必有
D．若满足且与同向，则
2．（2023·北京大兴·校考三模）设，是非零向量，“”是“”的（ ）
A．充分而不必要条件B．必要而不充分条件
C．充分必要条件D．既不充分也不必要条件
考点二、平面向量线性运算的综合考查
1．（2020·新高考全国2卷·高考真题）在中，D是AB边上的中点，则=（ ）
A．B．C．D．
2．（安徽·高考真题）若，, 则（ ）
A．（1，1）B．（－1，－1）C．（3，7）D．（-3,-7）
3．（北京·高考真题）已知是所在平面内一点，为边中点，且，那么（ ）
A．B．
C．D．
4．（上海·高考真题）在平行四边形中，下列结论错误的是（ ）
A．B．
C．D．
5．（福建·高考真题）设M为平行四边形ABCD对角线的交点，O为平行四边形ABCD所在平面内任意一点，则等于
A．B．C．D．
6．（四川·高考真题）如图，正六边形中，（ ）
A．B．C．D．
1．（2023·山东枣庄·统考模拟预测）如图，在长方体中，化简（ ）
A．B．C．D．
2．（2023·浙江·统考二模）设是平行四边形的对角线的交点，则（ ）
A．B．C．D．
考点三、平面向量共线定理及平行向量（共线向量）坐标运算的综合考查
1．（宁夏·高考真题）平面向量，共线的充要条件是
A．，方向相同
B．，两向量中至少有一个为零向量
C．，
D．存在不全为零的实数，，
2．（山东·高考真题）已知向量、满足，，，则一定共线的三点是
A．A，B，DB．A，B，CC．B，C，DD．A，C，D
3．（海南·高考真题）平面向量，共线的充要条件是（ ）
A．，方向相同B．，两向量中至少有一个为零向量
C．，D．存在不全为零的实数，，
4．（广东·高考真题）已知平面向量，，且，则等于（ ）
A．（-2，-4）B．（-3，-6）C．（-5，-10）D．（-4，-8）
5．（福建·高考真题）已知向量，，且，则 ．
6．（全国·高考真题）已知向量，，．若，则 ．
1．（2023·河南·襄城高中校联考三模）已知向量，若，则实数（ ）
A．5B．4C．3D．2
2．（2023·江苏盐城·统考三模）已知是平面四边形，设：，：是梯形，则是的条件（ ）
A．充分不必要B．必要不充分C．充要D．既不充分也不必要
3．（2023·黑龙江哈尔滨·哈尔滨三中校考模拟预测）在平面直角坐标系中，向量，，，若A，B，C三点共线，则的值为（ ）
A．B．C．D．
4．（2023·甘肃兰州·兰州五十九中校考模拟预测）已知向量，，．若，则实数的值为（ ）
A．B．C．D．
5．（2023·宁夏石嘴山·石嘴山市第三中学校考一模）设向量不平行，向量与平行，则实数（ ）
A．B．C．D．
6．（2023·山西临汾·统考一模）已知，为不共线的非零向量，，，，则（ ）
A．，，三点共线B．，，三点共线
C．，，三点共线D．，，三点共线
7．（2023·全国·模拟预测）（多选）有关平面向量的说法，下列错误的是（ ）
A．若，，则B．若与共线且模长相等，则
C．若且与方向相同，则D．恒成立
【基础过关】
一、单选题
1．（2023·河北·高三学业考试）化简所得的结果是（ ）
A．B．C．D．
2．（2023·全国·高三对口高考）如图正六边形中，（ ）

A．B．C．D．
3．（2023·河北·高三学业考试）如图，正六边形中，（ ）
A．B．C．D．
4．（2023·全国·高三对口高考）给出下列四个命题：
①若，则；
②若，则A，B，C，D是一个平行四边形的四个顶点；
③若，则；
④若，，则；
其中正确的命题的个数为（ ）
A．4B．3C．2D．1
二、多选题
5．（2023·全国·高三专题练习）给出下面四个结论，其中正确的结论是（ ）
A．若线段，则向量
B．若向量，则线段
C．若向量与共线，则线段
D．若向量与反向共线，则
三、填空题
6．（2023·河南·统考二模）已知不共线，向量，，且，则 ．
7．（2023·海南·校联考模拟预测）已知向量，，，若点，，三点共线，则实数 ．
8．（2023·四川成都·石室中学校考模拟预测），是两个不共线的向量，已知，，且三点共线，则实数 .
9．（2023·全国·高三专题练习）设，是两个不共线的非零向量，若向量与的方向相反，则 .
10．（2023·全国·高三对口高考）已知，则与向量平行的单位向量的坐标为 ．
【能力提升】
一、单选题
1．（2023·全国·高三专题练习）已知，且三点共线，则（ ）
A．B．C．D．
2．（2023·全国·高三专题练习）已知为坐标原点，，若、，则与共线的单位向量为（ ）
A．B．或
C．或D．
3．（2023·全国·高三专题练习）若都为非零向量，则“”是“与共线”的（ ）
A．充要条件B．充分不必要条件
C．必要不充分条件D．既不充分也不必要条件
4．（2023春·浙江金华·高三浙江金华第一中学校考阶段练习）已知为单位向量，则“”是“存在，使得”的（ ）
A．充分而不必要条件B．必要而不充分条件
C．充分必要条件D．既不充分也不必要条件
5．（2023·湖南长沙·雅礼中学校考一模）下列说法正确的是（ ）
A．若，则与的方向相同或者相反
B．若，为非零向量，且，则与共线
C．若，则存在唯一的实数使得
D．若，是两个单位向量，且．则
6．（2023·河北·校联考三模）对于平面内个起点相同的单位向量，若每个向量与其相邻向量的夹角均为，则与的位置关系为（ ）
A．垂直B．反向平行C．同向平行D．无法确定
二、填空题
7．（2023春·安徽滁州·高三校考开学考试）已知向量，，且，则 .
8．（2023·全国·高三专题练习）已知，，，若向量，且与的夹角为钝角，写出一个满足条件的的坐标为 ．
9．（2023·广西玉林·统考三模）记数列的前n项和为，已知向量，，若，且，则通项为 ．
10．（2023·全国·高三专题练习）已知向量，，．若，则= ．
向量运算
定义
法则(或几何意义)
运算律
加法
求两个向量和的运算
交换律：a＋b＝b＋a；
结合律：
(a＋b)＋c＝a＋(b＋c)
减法
求a与b的相反向量－b的和的运算
a－b＝a＋(－b)
数乘
求实数λ与向量a的积的运算
|λ a|＝|λ||a|，当λ>0时，λa与a的方向相同；当λ