新高考数学一轮复习精品讲练测第6章第03讲 等比数列及其前n项和（2份，原卷版+解析版）

这是一份新高考数学一轮复习精品讲练测第6章第03讲 等比数列及其前n项和（2份，原卷版+解析版），文件包含新高考数学一轮复习精品讲练测第6章第03讲等比数列及其前n项和教师版doc、新高考数学一轮复习精品讲练测第6章第03讲等比数列及其前n项和学生版doc等2份试卷配套教学资源，其中试卷共70页， 欢迎下载使用。

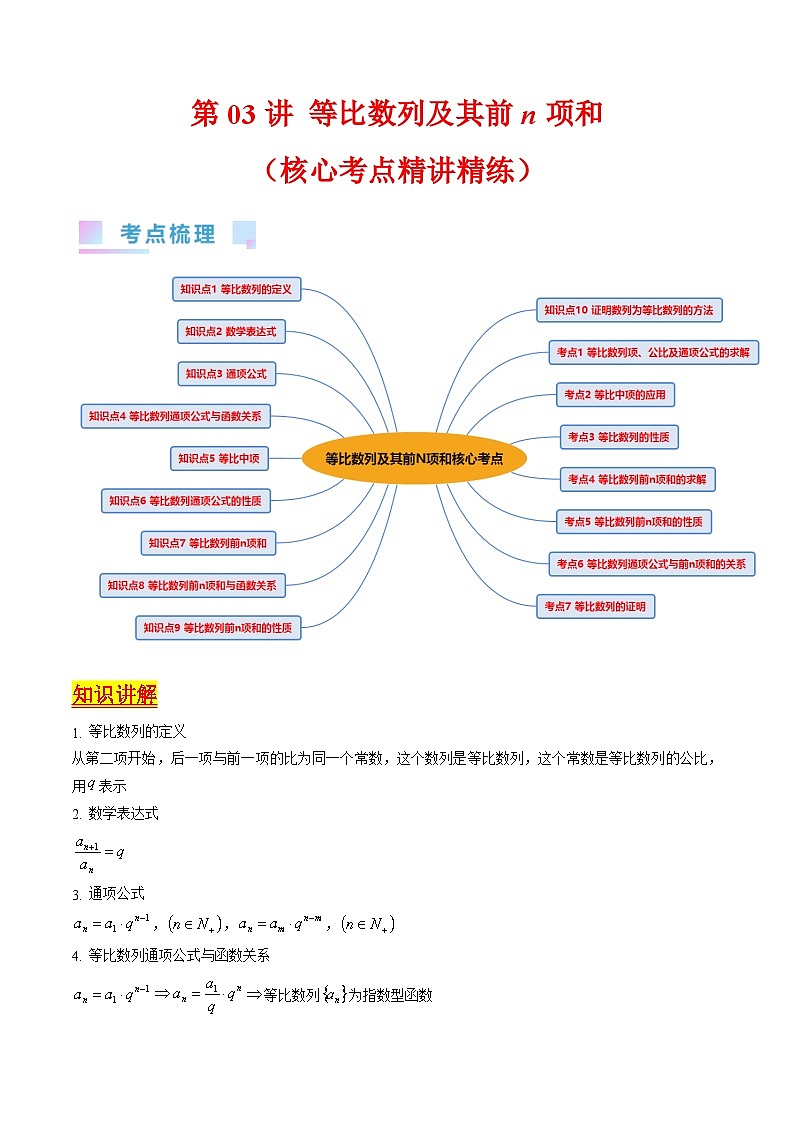
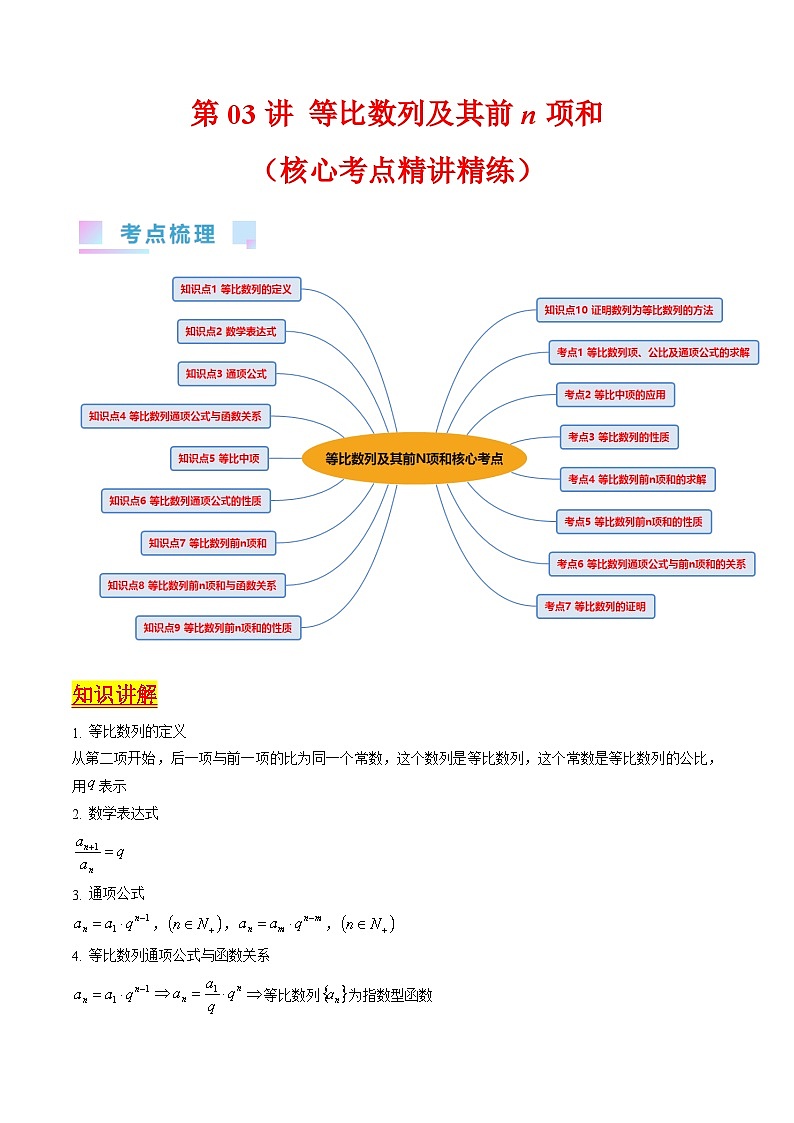
知识讲解
等比数列的定义
从第二项开始，后一项与前一项的比为同一个常数，这个数列是等比数列，这个常数是等比数列的公比，用表示
数学表达式
通项公式
，，，
等比数列通项公式与函数关系
等比数列为指数型函数
等比中项
若，，三个数成等比数列，则,其中叫做，的等比中项
等比数列通项公式的性质
（1）若或
（2）若，为等比数列，则，仍为等比数列
等比数列前n项和
等比数列前n项和与函数关系
等比数列前项和公式是指数型函数
等比数列前n项和的性质
（1），，……仍成等比数列
（2）
证明数列为等比数列的方法
（1）（为常数）为等比数列
（2）若,则，，三个数成等比数列
考点一、等比数列项、公比及通项公式的求解
1．（2020·山东·统考高考真题）在等比数列中，，，则等于（ ）
A．256B．-256C．512D．-512
2．（2022·全国·统考高考真题）已知等比数列的前3项和为168，，则（ ）
A．14B．12C．6D．3
3．（2020·海南·高考真题）已知公比大于的等比数列满足．
（1）求的通项公式；
（2）求.
1．（2023·四川成都·成都七中校考模拟预测）设是等比数列，且，，则（ ）
A．8B．-8C．4D．-4
2．（2022·云南·统考模拟预测）在等比数列中，，.
(1)求的通项公式；
(2)记为的前项和，若，求.
考点二、等比中项的应用之等差等比混考类型
1．（2023·河北·校联考三模）若数列为等比数列，则 ．
2．（2023·江西·统考模拟预测）已知数列满足，若，则 ．
3．（2023·重庆·校联考三模）已知是等差数列，是等比数列，若，，则（ ）
A．B．C．D．
4．（2023·山东济南·校考模拟预测）已知公差不为零的等差数列满足：，且成等比数列，则（ ）
A．B．C．D．
5．（2023·江西赣州·统考模拟预测）已知正项等比数列}满足为与的等比中项，则（ ）
A．B．C．D．2
1．（2023·四川成都·石室中学校考模拟预测）已知数列满足，，若，，则的值为 .
2．（2023·湖北·统考二模）已知数列是等差数列，数列是等比数列，若，，则（ ）
A．B．C．D．
3．（2023·福建泉州·泉州五中校考模拟预测）已知等差数列的公差不为0，且，，成等比数列，则（ ）
A．B．C．D．
4．（2023·重庆·重庆南开中学校考模拟预测）是公差不为零的等差数列，前项和为，若，，，成等比数列，则 .
5．（2022·全国·统考高考真题）记为数列的前n项和．已知．
(1)证明：是等差数列；
(2)若成等比数列，求的最小值．
考点三、等比数列的性质
1．（全国·高考真题）已知等比数列的各项均为正数，且，则（ ）
A．12B．10C．8D．
2．（全国·高考真题）已知各项均为正数的等比数列{}，=5，=10，则=
A．B．7C．6D．
3．（2023·云南·云南师大附中校考模拟预测）已知为递增的等比数列，且满足，，则（ ）
A．B．1C．16D．32
4．（2023·福建福州·福建省福州第一中学校考二模）已知等比数列满足，则（ ）
A．B．C．D．3
5．（2023·海南省直辖县级单位·统考模拟预测）在等比数列中，，，则 ．
1．（2023·安徽安庆·安庆一中校考三模）在等比数列中，，则（ ）
A．4B．8C．32D．64
2．（2023·贵州·校联考模拟预测）在等比数列中，，，则（ ）
A．3B．6C．9D．18
3．（2023·河南郑州·统考一模）在等比数列中，公比，且，则（ ）
A．3B．12C．18D．24
4．（2014·广东·高考真题）若等比数列的各项均为正数，且，则 .
考点四、等比数列前项和的求解
1．（2023·全国·统考高考真题）设等比数列的各项均为正数，前n项和，若，，则（ ）
A．B．C．15D．40
2．（2023·全国·统考高考真题）记为等比数列的前项和．若，则的公比为 ．
3．（2023·陕西宝鸡·统考二模）已知是等比数列的前项和，且，则（ ）
A．B．C．D．
1．（2023·湖北武汉·统考模拟预测）设等比数列的前项和为，已知，，则（ ）
A．80B．160C．121D．242
2．（2023·河北沧州·校考模拟预测）已知公比不为1的等比数列满足，则（ ）
A．40B．81C．121D．156
3．（2023·湖南长沙·周南中学校考二模）设等比数列的前项和为，已知，，则（ ）
A．B．C．D．
4．（2023·河北·统考模拟预测）已知等比数列的首项，公比，，且，则的前2023项和为 .
考点五、等比数列前项和的性质
1．（2021·全国·高考真题）记为等比数列的前n项和.若，，则（ ）
A．7B．8C．9D．10
2．（2020·全国·统考高考真题）设是等比数列，且，，则（ ）
A．12B．24C．30D．32
3．（2023·全国·统考高考真题）记为等比数列的前n项和，若，，则（ ）．
A．120B．85C．D．
4．（2023·广西玉林·统考三模）已知等比数列的前n项和为，若，则（ ）
A．12B．36C．31D．33
5．（2023·湖北武汉·统考三模）（多选）已知实数数列的前n项和为，下列说法正确的是（ ）．
A．若数列为等差数列，则恒成立
B．若数列为等差数列，则，，，…为等差数列
C．若数列为等比数列，且，，则
D．若数列为等比数列，则，，，…为等比数列
1．（2023·宁夏银川·校考模拟预测）设等比数列中，前n项和为，已知，，则等于（ ）
A．B．
C．D．
2．（2023·辽宁大连·校考模拟预测）等比数列的前n项和为，若，，则（ ）
A．60B．70C．80D．150
3．（2023·陕西榆林·统考模拟预测）已知等比数列的前项和为，若，则（ ）
A．41B．45C．36D．43
4．（2023·湖南长沙·周南中学校考三模）（多选）已知数列的前n项和是，则下列说法正确的是（ ）
A．若，则是等差数列
B．若，，则是等比数列
C．若是等差数列，则，，成等差数列
D．若是等比数列，则，，成等比数列
5．（2023·河北沧州·统考模拟预测）已知等比数列的前项和为，若，，则 .
考点六、等比数列通项公式与前项和的关系
1．（2023·四川泸州·四川省泸县第四中学校考模拟预测）设为数列的前项和，若，，则下列各选项在正确的是（ ）
A．B．
C．D．
2．（2021·浙江·统考高考真题）已知数列的前n项和为，，且.
（1）求数列的通项；
（2）设数列满足，记的前n项和为，若对任意恒成立，求实数的取值范围.
3．（2023·广东韶关·统考模拟预测）设等比数列的前项和为，已知，.
(1)求数列的通项公式；
(2)设，求数列的前项和.
1．（全国·高考真题）若数列{an}的前n项和为Sn＝an＋，则数列{an}的通项公式是an= .
2．（浙江·高考真题）设数列{}的前项和为.已知=4，=2+1，.
（Ⅰ）求通项公式；
（Ⅱ）求数列{||}的前项和.
3．（2023·福建福州·福建省福州第一中学校考二模）已知数列的前项和为，满足.
(1)求数列的通项公式；
(2)记，求数列的前项和.
考点七、等比数列的证明
1．（2023·重庆巴南·统考一模）已知数列的首项，且满足.
(1)求证：是等比数列；
(2)求数列的前项和.
2．（2023·福建福州·福建省福州第一中学校考模拟预测）已知数列的首项，，.
(1)设，求数列的通项公式；
(2)在与（其中）之间插入个3，使它们和原数列的项构成一个新的数列.记为数列的前n项和，求.
3．（2023·江西赣州·统考模拟预测）设数列的前项和为，且，，，.
(1)证明：数列为等比数列；
(2)设，求数列的前n项和.
4．（2023·全国·模拟预测）记为数列的前n项和，，．
(1)证明：数列为等比数列；
(2)若，求数列的前n项和．
1．（2023·广东·校联考模拟预测）记为数列的前项和，已知的等差中项为.
(1)求证为等比数列；
(2)数列的前项和为，是否存在整数满足？若存在求，否则说明理由.
2．（2023·江西宜春·校联考模拟预测）已知数列中，，．
(1)求的通项公式；
(2)若数列中，，证明：，（）．
3．（2023·广东梅州·统考三模）已知数列满足，，.
(1)证明：数列为等比数列.
(2)数列满足，求数列的前项和.
4．（2023·西藏日喀则·统考一模）已知数列的前项和为，且.
(1)求，并求数列的通项公式；
(2)若，求数列的前项和.
【基础过关】
一、单选题
1．（2023·北京房山·统考二模）已知等比数列的各项均为正数，的前项和为，若，，则的值为（ ）
A．B．C．D．
2．（2023·全国·模拟预测）已知等比数列的前项和为，若，，则（ ）
A．B．C．D．
3．（2023·宁夏石嘴山·石嘴山市第三中学校考模拟预测）在递增等比数列中，其前项和为，且是和的等差中项，则（ ）
A．28B．20C．18D．12
4．（2023·黑龙江哈尔滨·哈尔滨市第六中学校校考二模）设等比数列，，是方程的两根，则的值是（ ）
A．或B．2或C．D．
5．（2023·河南新乡·统考三模）已知公差不为零的等差数列中，，且，，成等比数列，是数列的前项和，则（ ）
A．45B．42C．84D．135
二、填空题
6．（2023·海南·校联考模拟预测）设等比数列的前项和为，若，则的公比为 .
7．（2023·浙江·二模）已知等比数列满足，则公比 .
8．（2023·河北·统考模拟预测）若数列为等比数列，，，则 ．
三、解答题
9．（2023·湖北·统考二模）设数列前n项和满足，．
(1)证明：数列为等比数列；
(2)记，求数列的前n项和．
10．（2023·四川·校联考一模）已知数列的前n项和为，且满足.
(1)证明：数列是等比数列；
(2)记，数列的前n项和为，求证：.
【能力提升】
一、单选题
1．（2023·河北唐山·开滦第二中学校考模拟预测）已知数列为等比数列，且，，则（ ）
A．30B．C．40D．
2．（2023·山东菏泽·山东省鄄城县第一中学校考三模）已知数列的前项和为，若满足，则（ ）
A．B．C．D．
3．（2023·四川南充·四川省南充高级中学校考模拟预测）已知数列 满足：，，，则（ ）
A．B．
C．D．
4．（2023·山东青岛·统考二模）设表示不超过的最大整数（例如：，），则（ ）
A．B．C．D．
5．（2023·山东潍坊·校考一模）已知是数列的前项和，且，（），则下列结论正确的是（ ）
A．数列为等比数列B．数列为等比数列
C．D．
二、解答题
6．（2023·广东梅州·大埔县虎山中学校考模拟预测）已知数列的前n项和为.
(1)若，，证明：；
(2)在（1）的条件下，若，数列的前n项和为，求证
7．（2023·广东东莞·校考三模）已知数列和，，，.
(1)求证数列是等比数列；
(2)求数列的前项和.
8．（2023·河南·襄城高中校联考三模）在等比数列中，，且，，成等差数列．
(1)求的通项公式；
(2)设，数列的前n项和为，求满足的k的值．
9．（2023·广西桂林·校考模拟预测）设数列的前项和为，且与的等差中项为.
(1)证明：数列是等比数列；
(2)设，证明：.
10．（2023·全国·模拟预测）已知数列中，是其前项的和，，.
(1)求，的值，并证明是等比数列；
(2)证明：.
【真题感知】
一、单选题
1．（2023·天津·统考高考真题）已知为等比数列，为数列的前项和，，则的值为（ ）
A．3B．18C．54D．152
2．（2020·全国·统考高考真题）记Sn为等比数列{an}的前n项和．若a5–a3=12，a6–a4=24，则=（ ）
A．2n–1B．2–21–nC．2–2n–1D．21–n–1
3．（2020·全国·统考高考真题）数列中，，对任意 ，若，则 （ ）
A．2B．3C．4D．5
二、多选题
4．（2021·全国·统考高考真题）设正整数，其中，记．则（ ）
A．B．
C．D．
三、双空题
5．（2023·北京·统考高考真题）我国度量衡的发展有着悠久的历史，战国时期就已经出现了类似于砝码的、用来测量物体质量的“环权”．已知9枚环权的质量（单位：铢）从小到大构成项数为9的数列，该数列的前3项成等差数列，后7项成等比数列，且，则 ；数列所有项的和为 ．
四、解答题
6．（2022·全国·统考高考真题）已知为等差数列，是公比为2的等比数列，且．
(1)证明：；
(2)求集合中元素个数．
7．（2020·全国·统考高考真题）设等比数列{an}满足，．
（1）求{an}的通项公式；
（2）记为数列{lg3an}的前n项和．若，求m．
8．（2020·天津·统考高考真题）已知为等差数列，为等比数列，．
（Ⅰ）求和的通项公式；
（Ⅱ）记的前项和为，求证：；
（Ⅲ）对任意的正整数，设求数列的前项和．
9．（2021·天津·统考高考真题）已知是公差为2的等差数列，其前8项和为64．是公比大于0的等比数列，．
（I）求和的通项公式；
（II）记，
（i）证明是等比数列；
（ii）证明
10．（2022·天津·统考高考真题）设是等差数列，是等比数列，且．
(1)求与的通项公式；
(2)设的前n项和为，求证：；
(3)求．