新高考数学一轮复习精品讲练测第7章第02讲 空间几何体的外接球与内切球（2份，原卷版+解析版）

这是一份新高考数学一轮复习精品讲练测第7章第02讲 空间几何体的外接球与内切球（2份，原卷版+解析版），文件包含新高考数学一轮复习精品讲练测第7章第02讲空间几何体的外接球与内切球教师版doc、新高考数学一轮复习精品讲练测第7章第02讲空间几何体的外接球与内切球学生版doc等2份试卷配套教学资源，其中试卷共130页， 欢迎下载使用。

知识讲解
球的表面积和体积公式
球的表面积：S＝4πR2 球的体积：V＝eq \f(4,3)πR3
球的切接概念
空间几何体的外接球：球心到各个顶点距离相等且等于半径的球是几何体的外接球
空间几何体的内切球：球心到各面距离相等且等于半径的球是几何体的内切球
几个与球有关的切、接常用结论
(1)正方体的棱长为a，球的半径为R，
①若球为正方体的外接球，则2R＝eq \r(3)a；
②若球为正方体的内切球，则2R＝a；
③若球与正方体的各棱相切，则2R＝eq \r(2)a.
(2)若长方体的同一顶点的三条棱长分别为a，b，c，外接球的半径为R，则2R＝eq \r(a2＋b2＋c2).
(3)正四面体的外接球与内切球的半径之比为3∶1.
墙角模型（三条直线两两垂直）
补形为长方体，长方体的同一顶点的三条棱长分别为a，b，c，外接球的半径为R，则2R＝eq \r(a2＋b2＋c2).
直棱柱外接球之汉堡模型
（1）补型：补成长方体，若各个顶点在长方体的顶点上，则外接球与长方体相同
（2）作图：构造直角三角形，利用勾股定理
直三校柱内接于一球（棱柱的上下底面为直角三角形）
底面外接圆的半径r的求法
（1）正弦定理
（2）直角三角形：半径等于斜边的一半
（3）等边三角形：半径等于三分之二高
（4）长（正）方形：半径等于对角线的一半
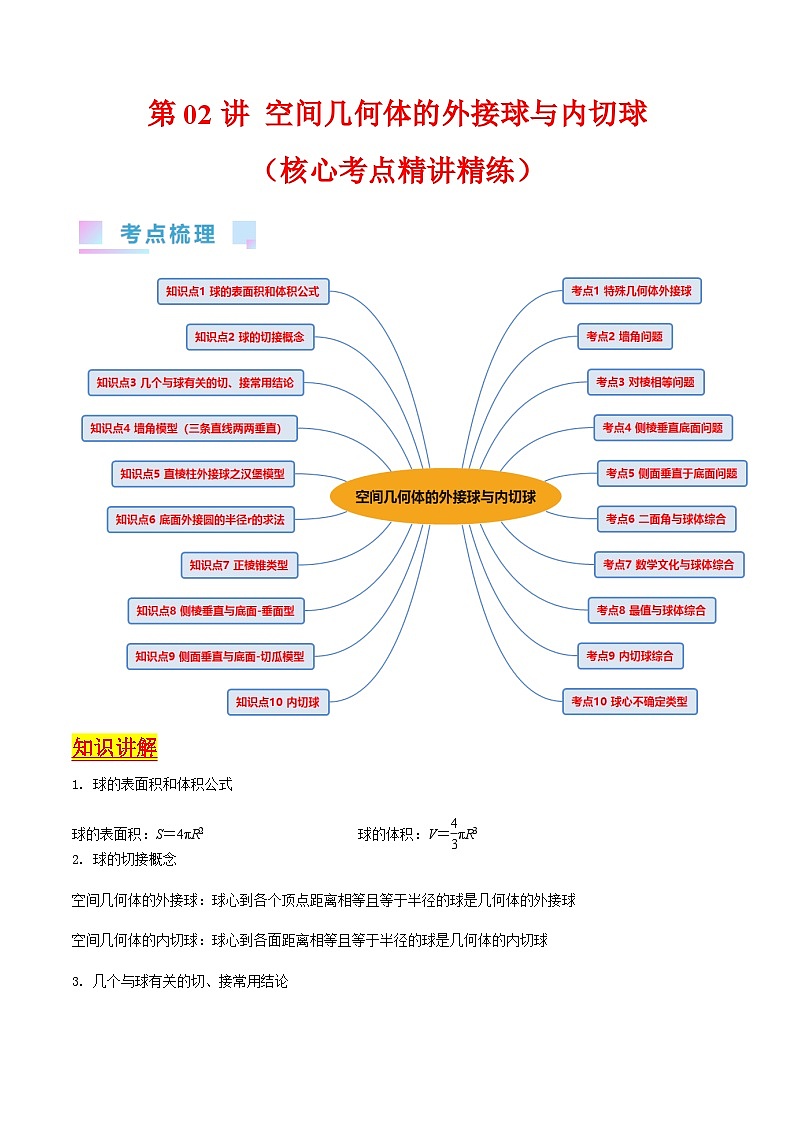
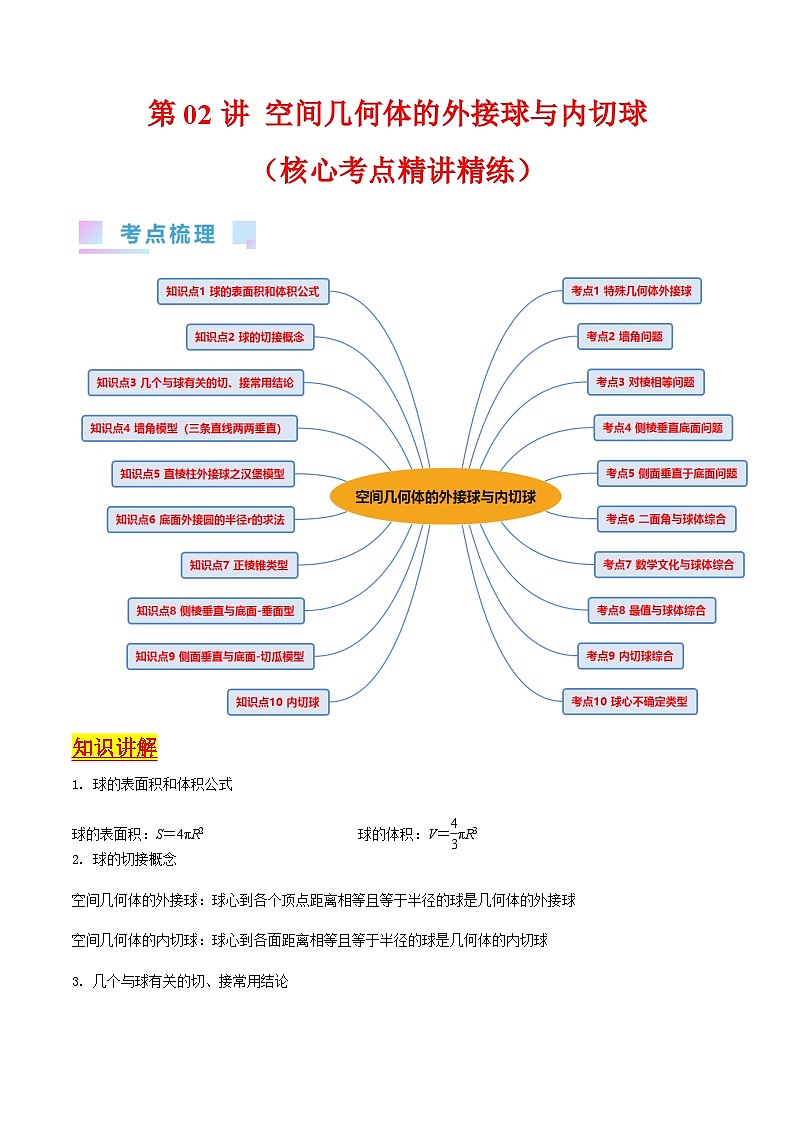
正棱锥类型
, 解出
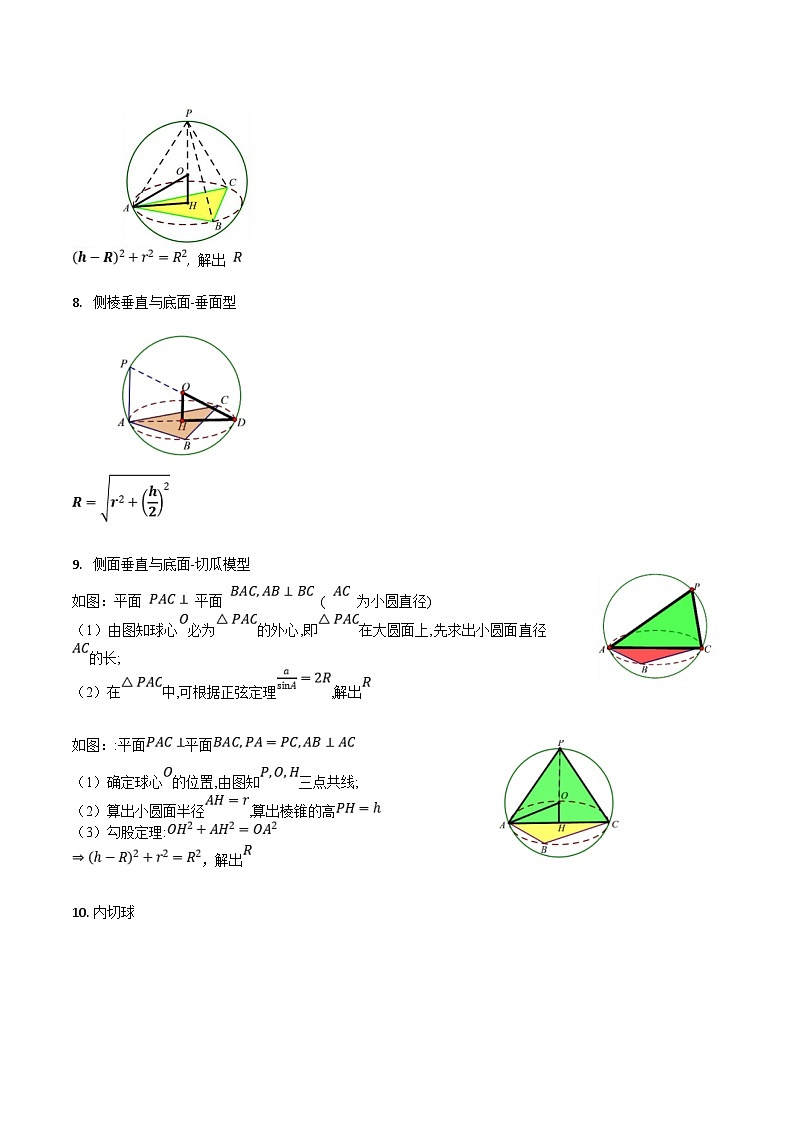
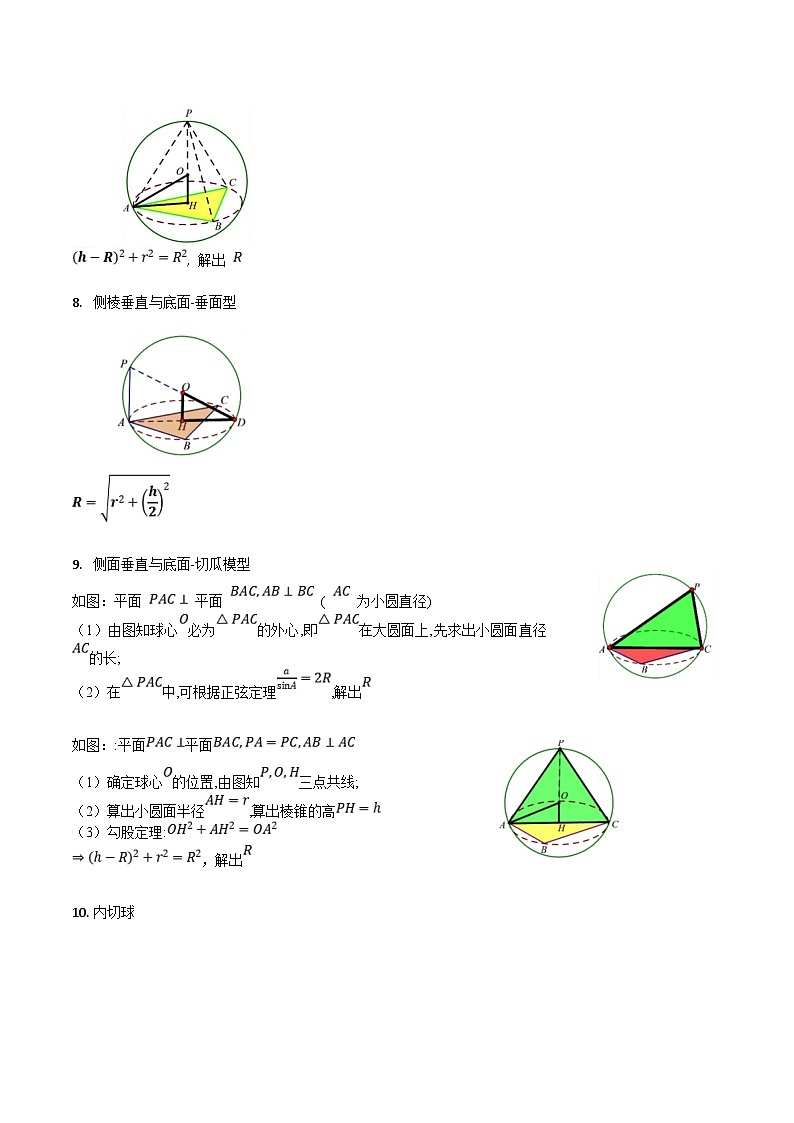
侧棱垂直与底面-垂面型
侧面垂直与底面-切瓜模型
如图：平面 平面 ( 为小圆直径)
（1）由图知球心必为的外心,即在大圆面上,先求出小圆面直径的长;
（2）在中,可根据正弦定理,解出
如图：:平面平面
（1）确定球心的位置,由图知三点共线;
（2）算出小圆面半径,算出棱锥的高
（3）勾股定理:
，解出
内切球
如图：求任意三棱雉的内切球半径(等体积法)
（1）先求出四个表面的面积和整个椎体的体积;
（2）设内切球半径为,建立等式:
（3）解出
结论：若棱锥的体积为V，表面积为S，则内切球的半径为.
考点一、特殊几何体外接球
1．（2023·全国·高三专题练习）长方体的长，宽，高分别为3，，1，其顶点都在球O的球面上，则球O的体积为（ ）
A．B．C．D．
【答案】A
【分析】求出长方体外接球半径，再由球体体积公式求体积.
【详解】球O的半径为，
∴体积．
故选：A
2．（2022·北京·101中学校考三模）一个底面积为1的正四棱柱的顶点都在同一球面上，若此球的表面积为，则该四棱柱的高为（ ）
A．B．2C．D．
【答案】C
【分析】根据球的表面积公式，可算出，由正四棱柱的顶点在同一球面上，可得正四棱柱体对角线恰好是球的一条直径，即可得到答案
【详解】设球的半径为，则 ，解得
设四棱柱的高为 ，则 ，解得
故选：C
3．（2022秋·广东江门·高三鹤山市鹤华中学校考开学考试）一平面截一球得到直径为的圆面，球心到这个平面的距离是，则该球的体积是（ ）
A．B．C．D．
【答案】B
【分析】作出过球心的截面，利用勾股定理可求得球的半径，由球的体积公式可求得结果.
【详解】设球心为，截面圆心为，连接，则垂直于截面圆，如图所示，
在中，，，
球的半径，球的体积．
故选：B.
4．（2023·贵州贵阳·校联考三模）已知一圆锥内接于球，圆锥的表面积是其底面面积的3倍，则圆锥与球的体积之比是（ ）
A．B．C．D．
【答案】B
【分析】首先利用圆锥的表面积是其底面面积的3倍以及直角三角形的性质，求出球的半径和圆锥的底面半径的关系，进一步求出圆锥的体积和球的体积的比值．
【详解】如图所示，设圆锥的底面圆圆心为点，延长与球面交于.
设圆锥底面半径为r，母线为l，则，得，
圆锥的高
设球半径为R，则中，
有，即，
即，
，故，
故选：B.

5．（2023·全国·校联考模拟预测）上、下底面均为等边三角形的三棱台的所有顶点都在同一球面上，若三棱台的高为，上、下底面边长分别为，，则该球的体积为（ ）
A．B．C．D．
【答案】A
【分析】设三棱台为，其中是下底面，是上底面，点，分别为，的中心，证明点就是几何体的外接球的球心，即得解.
【详解】设三棱台为，其中是下底面，是上底面，点，分别为，的中心，
则，，同理，
所以，同理.
所以.
所以点就是几何体的外接球的球心.
所以球半径，
所以体积为．
故选：A
1．（2023·全国·高三专题练习）长方体的长、宽、高分别为2，2，1，其顶点都在球的球面上，则球的表面积为 .
【答案】
【分析】根据长方体的体对角线为其外接球的直径即可求解.
【详解】因为长方体的外接球的直径为长方体的体对角线，长方体的长、宽、高分别为2，2，1，
所以长方体的外接球的直径，
故长方体的外接球的半径为，
所以球的表面积为.
故答案为：
2．（2022·内蒙古巴彦淖尔·校考一模）一个正方体的顶点都在同一个球的球面上，该正方体的棱长为a，则球的表面积是（ ）
A．B．C．D．
【答案】D
【分析】先求得球的半径，再利用球的表面积公式即可求得该球的表面积
【详解】正方体的对角线是球的直径，所以，则，
所以球的表面积
故选：D.
3．（2023·湖北·统考二模）已知直三棱柱存在内切球，若，则该三棱柱外接球的表面积为（ ）
A．B．C．D．
【答案】D
【分析】求出直三棱柱的高后可求其外接球的半径，从而可求外接球的表面积.
【详解】因为，故，
故的内切圆的半径为.
因为直三棱柱存在内切球，故直三棱柱的高即为内切球的直径.
而内切球的半径即为底面三角形内切圆的半径，故内切球的半径为1，
故直三棱柱的高为2.
将直三棱柱补成如图所示的长方体，则外接球的直径即为该长方体的体对角线，
故外接球的半径为，
故外接球的的表面积为.
故选：D.
4．（2023·福建泉州·校联考模拟预测）已知正四棱台的高为，下底面边长为，侧棱与底面所成的角为，其顶点都在同一球面上，则该球的体积为（ ）
A．B．
C．D．
【答案】B
【分析】连接，过作的垂线垂足为，过作的垂线垂足为，求得上、下底面所在圆的半径，设球心到上下底面的距离分别为，球的半径为，利用球的截面圆的性质，列出方程求得，结合球的体积公式，即可求解.
【详解】设正四棱台上下底面所在圆面的半径分别为，连接，
过作的垂线垂足为，过作的垂线垂足为，
因为正四棱台的高为，下底面边长为，侧棱与底面所成的角为，
可得，即，
设球心到上下底面的距离分别为，球的半径为，
可得，，故或，
即或，解得，符合题意，
所以球的体积为．
故选：B.
考点二、墙角问题
1．（2023·天津·校考模拟预测）已知三棱锥的三条侧棱两两互相垂直，且，则此三棱锥的外接球的体积为
A．B．C．D．
【答案】B
【详解】由题意可知：可将三棱锥放入长方体中考虑，则长方体的外接球即三棱锥的外接球，故球的半径为长方体体对角线的一半，设，则，故,得球的体积为：
2．（2021春·广西柳州·高三柳铁一中校考阶段练习）已知三棱锥的四个顶点都在球的表面上， 平面，且，则球的表面积为
A．B．C．D．
【答案】C
【详解】由题意可知CA,CB,CD两两垂直，所以补形为长方形，三棱锥与长方体共球，，求的外接球的表面积，选C
【点睛】求共点三条侧棱两两垂直的三棱锥外接球相关问题，我们常用的方法为补形成长方体，转化为求长方体的外接球问题．充分体现补形转化思想．
3．（2023·天津河西·统考二模）在三棱锥中，平面，，，，则三棱锥外接球的表面积为（ ）
A．B．C．D．
【答案】C
【分析】三棱锥补成长方体，计算出长方体的体对角线长，即为三棱锥的外接球直径长，再利用球体表面积公式可求得结果.
【详解】在三棱锥中，平面，，，，
将三棱锥补成长方体，如下图所示，
所以，三棱锥的外接球直径即为长方体的体对角线长，
设三棱锥的外接球直径为，则，则，
因此，三棱锥外接球的表面积为.
故选：C.
1．（2022·四川达州·统考二模）四面体的每个顶点都在球的球面上，两两垂直，且，，，则球的表面积为（ ）
A．B．C．D．
【答案】B
【分析】根据几何体特征可知球即为以为长、宽、高的长方体的外接球，根据长方体外接球半径为体对角线长一半可求得球的半径，由球的表面积公式可得结果.
【详解】四面体的外接球即为以为长、宽、高的长方体的外接球，
球的外接球半径，
球的表面积.
故选：B.
2．（2023·四川成都·石室中学校考三模）若三棱锥P-ABC的所有顶点都在同一个球的表面上，其中PA⊥平面ABC，，，，则该球的体积为（ ）
A．B．C．D．
【答案】D
【分析】先补形为长方体，再根据长方体外接球计算球的体积即可.
【详解】因为PA⊥平面ABC，，所以可将该三棱锥进行补形，补成一个长方体，
从而长方体的外接球就是该三棱锥的外接球，
则外接球的直径为，得，
故三棱锥P-ABC的外接球的体积为.
故选：D.
考点三、对棱相等问题
1．（2023·辽宁·鞍山一中校联考模拟预测）在三棱锥中，，，，则三棱锥的外接球的表面积为（ ）
A．B．C．D．
【答案】A
【分析】根据给定条件，构造面对角线长分别为4，5，的长方体，求出其体对角线长即可求解作答.
【详解】三棱锥中，，，，
构造长方体，使得面上的对角线长分别为4，5，，则长方体的对角线长等于三棱锥外接球的直径，如图，
设长方体的棱长分别为，，，则，，，则，
因此三棱锥外接球的直径为，
所以三棱锥外接球的表面积为．
故选：A
2．（2023·甘肃张掖·统考模拟预测）在四面体中，，则四面体外接球表面积是（ ）
A．B．C．D．
【答案】B
【分析】利用割补法及勾股定理，结合长方体的体对角线是外接球的直径及球的表面积公式即可求解.
【详解】由题意可知，此四面体可以看成一个长方体的一部分，长方体的长、宽、高分别为，，，四面体如图所示，
所以此四面体的外接球的直径为长方体的体对角线，即,解得.
所以四面体外接球表面积是.
故答案为：B.
3．（2023·河南·开封高中校考模拟预测）已知四面体ABCD中，，，，则四面体ABCD外接球的体积为（ ）
A．B．C．D．
【答案】C
【分析】构造一个长方体，四面体四个顶点在长方体顶点上，利用长方体的对角线为外接球直径求解即可.
【详解】设四面体的外接球的半径为,
则四面体在一个长宽高为的长方体中，如图，
则 故，
故四面体ABCD外接球的体积为，
故选：C
1．（2023·四川成都·树德中学校考三模）已知三棱锥的四个顶点都在球的球面上，，，则球的表面积为（ ）
A．B．C．D．
【答案】A
【分析】根据给定条件，证明平面，再确定球心O的位置，求出球半径作答.
【详解】在三棱锥中，如图，，则，同理，
而平面，因此平面，
在等腰中，，则，，
令的外接圆圆心为，则平面，，
有，取中点D，连接OD，则有，又平面，即，
从而，四边形为平行四边形，，又，
因此球O的半径，
所以球的表面积.
故选：A
2．（2023·江西·统考模拟预测）在三棱锥中，已知，则三棱锥外接球的表面积为（ ）
A．B．C．D．
【答案】A
【分析】因为三棱锥的对棱相等，所以可以把它看成长方体的面对角线长,根据长方体外接球直径是体对角线求解即可.
【详解】因为三棱锥的对棱相等，所以可以把它看成长方体的面对角线，
设长方体的同一顶点三条棱长分别为,且长方体的面对角线长为，
则,
长方体体对角线为长方体外接球直径，即为三棱锥外接球的直径，
，它外接球半径等于，
所以球的表面积为.
故选:A.
3．（2023·全国·模拟预测）在三棱锥中，已知，，，则下列结论错误的是（ ）
A．异面直线与所成角的余弦值为
B．异面直线与所成角的余弦值为
C．三棱锥外接球的表面积为
D．直线与平面所成角的正弦值为
【答案】D
【分析】将三棱锥补形成长方体，求出长方体的长、宽、高，建立空间直角坐标系，表达出各点的坐标，在长方体中进行向量的计算，即可判断各选项的正误．
【详解】由题意，在三棱锥中，已知，，，
∴可将三棱锥补形成长方体，建立空间直角坐标系如下图所示：
由几何知识得，,,，
解得，，．
则，，，．
对于A：，，
所以，
所以异面直线AB与PC所成角的余弦值为，故A正确．
对于B：，，
所以,
所以异面直线BC与PA所成角的余弦值为，故B正确．
对于C：易知三棱锥外接球的半径
所以三棱锥P-ABC外接球的表面积，故C正确．
对于D：设平面PBC的法向量为，则,即，
取，得，，所以，
设直线与平面所成的角为，则，故D错误．
故选：D.
考点四、侧棱垂直底面问题
1．（2023·宁夏银川·宁夏育才中学校考三模）三棱锥中，，，则三棱锥的外接球的表面积为（ ）
A．B．C．D．
【答案】C
【分析】根据题意可将三棱锥补形为长方体，则三棱锥的外接球即为长方体的外接球，根据长方体的性质求外接球的半径，即可得结果.
【详解】如图所示，根据题意可将三棱锥补形为长方体，则三棱锥的外接球即为长方体的外接球，可知该球的直径即为，
设球的半径为，可得，即，
故三棱锥的外接球的表面积.
故选：C.
2．（2023·广西柳州·柳州高级中学校联考模拟预测）在三棱锥P－ABC中，，，且，，，，则此三棱锥外接球的体积为（ ）
A．B．C．D．
【答案】B
【分析】由已知求得，根据勾股定理证明得到，进而推得平面，则该三棱锥可以看作是长方体的一部分，求出长方体的体对角线长，即可得出外接球的半径，进而根据体积公式，即可得出答案.
【详解】如图1，
因为，，，
所以.
又，，
所以在中，有，
所以，，即.
又，平面，平面，，
所以平面.
则该三棱锥可以看作是长方体的一部分，如图2
其中，，，，
则，
所以此三棱锥外接球的半径为，
所以，此三棱锥外接球的体积为.
故选：B.
3．（2023·山东德州·三模）在四棱锥中，底面为矩形，平面，点为上靠近的三等分点，则三棱锥外接球的表面积为（ ）
A．B．C．D．
【答案】A
【分析】利用正弦定理可得三角形的外接圆半径为，根据勾股定理即可求解外接球半径，进而可求表面积.
【详解】由题意可得
所以在三角形中，由等面积法可得,
设三角形的外接圆半径为，圆心为,则由正弦定理得，
由于平面,设三棱锥外接球的半径为,球心到平面的距离为，
过作,则，因此,
故外接球的表面积为,
故选：A

1．（2023·山西吕梁·统考二模）在三棱锥中，已知底面，，，则三棱锥外接球的体积为（ ）
A．B．C．D．
【答案】B
【分析】设中点，中点，由直角三角形外接圆为斜边中点，且由题意可知，所以底面，则为三棱锥外接球的球心，可解.
【详解】设中点，中点，
由，，所以的外接圆直径，
且圆心为，
由于底面，，所以底面，
则为三棱锥外接球的球心，
所以外接球的直径，
所以外接球的体积．
故选：B

2．（2023·海南·统考模拟预测）已知三棱锥的四个顶点都在球的球面上，平面，在底面中，，，若球的体积为，则（ ）
A．1B．C．D．2
【答案】A
【分析】由球体积公式求球体半径，正余弦定理求外接圆半径，结合线面垂直模型求即可.
【详解】由题意，设球的半径为，则，
由，
外接圆半径，
根据线面垂直模型知：.

故选：A
3．（2023·四川·校联考模拟预测）在三棱锥中，平面，则三棱锥的外接球的表面积为（ ）
A．B．C．D．
【答案】A
【分析】先用正弦定理求出外接圆的半径，然后利用求出三棱锥外接球的半径，即可算出表面积.
【详解】设外接圆的半径为，圆心为，
根据正弦定理，则，故，
设三棱锥外接球的半径为，球心为O，

由，可知为等腰三角形，
过作于，则为中点，由平面，平面，
故，则共面，
因为平面，平面，所以，
又，故，于是四边形为平行四边形，
因为，所以四边形为为矩形，
则，故三棱锥的外接球的表面积为.
故选：A.
4．（2023·江西·江西师大附中校考三模）已知正方体的棱长为2，为棱上的一点，且满足平面平面，则四面体的外接球的表面积为（ ）
A．B．C．D．
【答案】A
【分析】确定平面，得到，根据勾股定理确定为中点，将四面体放入长方体中，计算半径得到表面积.
【详解】如图所示：为的中点，连接，，，

，则，平面，平面平面，
平面平面，故平面，
平面，故，
设，则，，，
，即，解得，
将四面体放入长方体中，
设四面体的外接球半径为，则，，
外接球的表面积.
故选：A.
考点五、侧面垂直于底面问题
1．（2023·贵州贵阳·校联考模拟预测）在三棱锥中，已知，且平面平面ABC，则三棱锥的外接球表面积为（ ）
A．B．C．D．
【答案】B
【分析】通过面面垂直确定球心的大致位置，在直角三角形中利用勾股定理可求球的半径，结合表面积公式可得答案.
【详解】如图，设外接球的半径为R，取AB的中点，连接，则由，得，
因为平面平面ABC，平面平面，平面，
所以平面ABC，则球心O在直线上．
连接OA，则，
因为，所以；
因为，所以.
因为，所以球心在线段上．
在中，由勾股定理，得，
即，解得，
所以三棱锥的外接球表面积为.
故选：B．
2．（2023·黑龙江大庆·统考二模）如图，边长为的正方形ABCD所在平面与矩形ABEF所在的平面垂直，，N为AF的中点，，则三棱锥外接球的表面积为（ ）

A．B．C．D．
【答案】A
【分析】根据题意得到平面ABEF，进一步得出，，则MC为外接球直径，代入球的表面积公式即可求解．
【详解】由可知，，，可求，，，
因为平面平面ABEF，平面平面，
又，平面，
所以平面ABEF，平面ABEF，所以，
由，，得，
又，同理可得得，又，
所以，所以.
所以MC为外接球直径，
在Rt△MBC中，即，
故外接球表面积为．
故选：A．
3．（2023·河南开封·统考三模）已知正方体的棱长为1，P为棱的中点，则四棱锥P－ABCD的外接球表面积为（ ）
A．B．C．D．
【答案】C
【分析】分别取三角形，四边形的外心，，利用正弦定理得到，即可得到，然后利用勾股定理得到，最后根据球的表面积公式求表面积即可.
【详解】
设四棱锥的外接球球心为，取中点，连接，取三角形，四边形的外心，，连接，，，，，
因为正方体的棱长为1，点为中点，所以，，，，，，所以，外接球的表面积.
故选：C.
4．（2023·河南郑州·校联考二模）如图，在三棱锥中，，，平面平面ABC，则三棱锥外接球的表面积为（ ）

A．B．C．D．
【答案】B
【分析】由题意说明为等腰直角三角形，根据面面垂直性质推出平面，进而结合球的几何性质，确定三棱锥外接球球心位置，求出外接球半径，即可求得答案.
【详解】由于，，故，
即为等腰直角三角形，
取AC的中点为M，连接，

因为，即为正三角形，故,
由于平面平面，平面平面，平面，
故平面，平面，故；
又M为的外心，
则三棱锥外接球的球心必在BM上，
设的中心为O，则O在BM上且，
而，
则，
即，
即O点即为三棱锥外接球的球心，
故外接球半径为，所以外接球表面积为，
故选：B
【点睛】关键点睛：解答本题的关键在于要能根据条件，结合球的几何性质，确定出三棱锥外接球球心的位置，进而求得半径.
1．（2023·四川达州·统考二模）三棱锥的所有顶点都在球O的表面上，平面平面BCD，，，，则球O的体积为（ ）
A．B．C．D．
【答案】A
【分析】取BD的中点O，根据条件得到和都是直角三角形，其外接圆的圆心都是，再根据平面平面BCD，得到O为外接球的球心求解.
【详解】解：如图所示：
取BD的中点O，
因为则是直角三角形，
因为。
所以是直角三角形，
所以和的外接圆的圆心都是，
又因为平面平面BCD，
所以O为外接球的球心，
因为，，
所以外接球的半径为，
所以外接球的体积为，
故选：A
2．（2023·全国·模拟预测）如图所示，已知三棱锥中，底面为等腰直角三角形，斜边，侧面为正三角形，D为的中点，底面，则三棱锥外接球的表面积为（ ）
A．B．C．D．
【答案】D
【分析】设三棱锥外接球的球心为O，确定球心的位置，即球心落在过底面外心的垂线上，利用图形的几何性质求得外接球半径，即可求得答案.
【详解】如图，设E是的中点，连接，D为的中点，故,
底面为等腰直角三角形，即,故；
设三棱锥外接球的球心为O，
连接，
因为底面为等腰直角三角形，E是的中点，
即E为的外心，故平面,
在等腰直角三角形中，斜边，则.
因为是正三角形，所以，
因为，所以三棱锥是正三棱锥，
所以O在底面上的射影F是的重心，
则点F在上，所以.
因为底面，故,
而底面，故,
又因为，平面,故平面，
而平面,故,
故四边形是矩形，所以，所以，
所以三棱锥外接球的半径，其表面积为，
故选：D.
3．（2023·江西九江·统考一模）三棱锥中，与均为边长为的等边三角形，若平面平面，则该三棱锥外接球的表面积为（ ）
A．B．C．D．
【答案】B
【分析】取中点，连接，，可得平面，平面，取的外心，的外心，分别过，作平面与平面的垂线交于点，即为球心，结合球的性质求得半径，可得三棱锥外接球的表面积.
【详解】
解：如图，取中点，连接，，则，，
因为平面平面，所以可得平面，平面，
取的外心，的外心，分别过作平面与平面的垂线交于点，即为球心，连接，
易得，，
，
.
故选：B.
考点六、二面角与球体综合
1．（2023·河南·襄城高中校联考三模）如图1，在中，，，，，沿将折起，使得二面角为60°，得到三棱锥，如图2，若，则三棱锥的外接球的表面积为（ ）

A．B．C．D．
【答案】A
【分析】先推出底面，，然后构造长方体找到三棱锥的球心为的中点，再计算可得结果.
【详解】因为，，，平面，平面，所以平面．
又平面，则，因为平面，平面，所以．
又，平面，平面，所以平面．
又平面，所以，即90°．因为为60°，所以60°，
在中，，可得，．
易知，的四个顶点可以与一个长方体的四个顶点重合，
如图所示，则该长方体的外接球即为的外接球，球心PC的中点，
，表面积为，故A正确．
故选：A.

2．（2023·甘肃张掖·高台县第一中学校考模拟预测）图1为两块大小不同的等腰直角三角形纸板组成的平面四边形ABCD，其中小三角形纸板的斜边AC与大三角形纸板的一条直角边长度相等，小三角形纸板的直角边长为a，现将小三角形纸板ACD沿着AC边折起，使得点D到达点M的位置，得到三棱锥，如图2．若二面角的大小为，则所得三棱锥M－ABC的外接球的表面积为（ ）

A．B．C．D．
【答案】C
【分析】先由线面垂直得出球心的位置，结合三角形中的计算求出球的半径，计算可得球的表面积.
【详解】如图，取AC的中点E，AB的中点F，连接ME，EF．
因为，所以．易知，因为，
所以，所以．
过点E作OE⊥平面MAC，过点F作OF⊥平面ABC，
，连接OA，易知E，F两点分别是△MAC和△ABC的外心，
所以点O是三棱锥的外接球的球心．
因为，所以，，
所以，因为，，
所以，所以，
又，所以，
则三棱锥的外接球的半径为，
所以外接球的表面积．

故选：C.
3．（2023·浙江·统考模拟预测）在四面体中，与都是边长为6的等边三角形，且二面角的大小为，则四面体外接球的表面积是（ ）
A．52πB．54πC．56πD．60π
【答案】A
【分析】三棱锥的外心必定在过一个三角形的外心与这个三角形所成的面垂直的垂线上，从而确定球心的位置，结合题意，利用几何关系求出外接球的半径，代入球的表面积公式，即可求解.
【详解】如图所示，取的中点，连接，分别取和的外心与，
过两点分别作平面和平面的垂线，交于点，
则就是外接球的球心，连接，
则为二面角的平面角，即，
则是等边三角形，其边长为，，
在中，，所以，
又由，所以，
所以四面体的外接球的表面积为.
故选：A.

1．（2023·广东·校联考模拟预测）已知四棱锥平面，二面角的大小为.若点均在球的表面上，则该球的表面积为（ ）
A．B．C．D．
【答案】B
【分析】先利用点均在球的表面上可得四点共圆，先证明平面，得出二面角的平面角为，可计算出，再利用勾股定理可得出四边形外接圆的直径为，则，最后利用外接球的表面积公式代入即可得出答案.
【详解】因为，所以，
因为点均在球的表面上，
所以四边形内接于圆，所以，所以，
因为平面，平面，所以，
又平面，所以平面，
平面，所以，又，
所以二面角的平面角为，所以，
在中，因为，所以，
由余弦定理可得：，
即，即或（舍去），
所以，所以外接圆的直径为：，
即四边形外接圆的直径为，
因为平面，所以，四棱锥外接球的半径为：
所以四面体外接球的表面积为.

故选：B.
2．（2023·浙江·校联考模拟预测）在三棱锥中，，，二面角的平面角为，则三棱锥外接球表面积的最小值为（ ）
A．B．
C．D．
【答案】B
【分析】取AC的中点M，可得即为二面角的平面角， △ACB的外心为O1，过O1作平面ABC的垂线，过△ACD的外心M作平面ACD的垂线，两条垂线均在平面BMD内，它们的交点就是球心O，在平面ABC内，设，然后表示出外接球的半径，利用基本不等式可求出其最小值，从而可求得答案.
【详解】当D在△ACD的外接圆上动的时候，该三棱锥的外接球不变，
故可使D点动到一个使得DA=DC的位置，取AC的中点M，连接，
因为，DA=DC，所以，，故即为二面角的平面角，
△ACB的外心为O1，过O1作平面ABC的垂线，过△ACD的外心M作平面ACD的垂线，两条垂线均在平面BMD内，它们的交点就是球心O，画出平面BMD，如图所示；
在平面ABC内，设，则，，
因为，所以，所以，
所以

令，则，
所以，当且仅当时取等，
故选:B
【点睛】关键点点睛：本题主要考查了三棱锥外接球的求法、三角函数的最值问题，解题的关键是根据题意找出外接球的球心位置，考察学生的空间想象能力和逻辑思维能力，考查学生的推理运算能力，属于难题.
考点七、数学文化与球体综合
1．（2023·天津南开·南开中学校考模拟预测）在《九章算术》中记载，堑堵是底面为直角三角形的直三棱柱，阳马指底面为矩形，一侧棱垂直于底面的四棱锥，鳖臑为四个面都为直角三角形的三棱锥，如图，在堑堵中，，鳖臑的外接球的体积为，则阳马体积的最大值为（ ）
A．B．C．D．4
【答案】B
【分析】设的外接球半径为r，根据鳖臑的外接球的体积即可求得r，再根据的外接球的半径与三棱柱的外接球的半径相同可得到x，y的关系式，再根据四棱锥的体积公式结合基本不等式即可求解．
【详解】设的外接球半径为r，
则的外接球的体积为．
．
又阳马的体积为，
所以阳马体积的最大值为．
故选：B．
2．（2023·广西南宁·南宁二中校考模拟预测）在《最强大脑》的节目中，作为脑力角逐的考题，阿基米德多面体成为了难倒一众天才的“元凶”，因此“一夜爆红”.“阿基米德多面体”也称半正多面体，是由边数不全相同的正多边形围成的多面体，它体现了数学的对称美.例如足球一般是有12个正五边形和20个正六边形构成的阿基米德多面体.如图是以一正方体的各条棱的中点为顶点的多面体，这是一个有八个面为正三角形，六个面为正方形的“阿基米德多面体”，若该多面体的棱长为1，则经过该多面体的各个顶点的球的表面积为（ ）

A．B．C．D．
【答案】C
【分析】根据给定条件，把多面体放在棱长为的正方体中，结合正方体的结构特征确定球心，求出球半径作答.
【详解】将该多面体放入正方体中，如图所示.

由于多面体的棱长为1，所以正方体的棱长为，
因为该多面体是由棱长为的正方体连接各棱中点所得，
所以该多面体外接球的球心为正方体对角线的中点，
其外接球直径等于正方体的面对角线长，即，所以，
所以经过该多面体的各个顶点的球的表面积.
故选：C
1．（2023·天津津南·天津市咸水沽第一中学校考模拟预测）《九章算术》中，称一个正方体内两个互相垂直的内切圆柱所围成的几何体为“牟合方盖”，现提供一中计算“牟合方盖”体积的方法，显然，正方体的内切球也是“牟合方盖”的内切球.因此，用任意平行于水平面的平面去截“牟合方盖”，截面均为正方形，平面截内切球得到上述正方形的内切圆，结合祖暅原理，利两个同高的立方体如在等高处的截面面积相等，则体积相等.若正方体棱长为3，则“牟合方盖”体积为（ ）

A．6B．12C．18D．24
【答案】C
【分析】先求得正方体内切球的体积，再由已知得出牟合方盖的体积.
【详解】正方体的棱长，则其内切球的半径为，
内切球的体积.
由于截面正方形与其内切圆的面积之比为.
设牟合方盖的体积为，则，从而牟合方盖的体积.
故选：C.
2．（2023·全国·模拟预测）中国古建筑闻名于世，源远流长．如图1所示的五脊殿是中国传统建筑中的一种屋顶形式，该屋顶的结构示意图如图2所示，在结构示意图中，已知四边形ABCD为矩形，，，与都是边长为1的等边三角形，若点A，B，C，D，E，F都在球O的球面上，则球O的表面积为（ ）
A．B．C．D．
【答案】D
【分析】如图，根据球的性质可得平面ABCD，根据中位线的性质和勾股定理可得且，分类讨论当O在线段上和O在线段的延长线上时2种情况，结合球的性质和表面积公式计算即可求解.
【详解】如图，连接AC，BD，设，
因为四边形ABCD为矩形，所以为矩形ABCD外接圆的圆心．连接，
则平面ABCD，分别取EF，AD，BC的中点M，P，Q，
根据几何体ABCDEF的对称性可知，直线交EF于点M．
连接PQ，则，且为PQ的中点，因为，所以，
连接EP，FQ，在与中，易知，
所以梯形EFQP为等腰梯形，所以，且．
设，球O的半径为R，连接OE，OA，
当O在线段上时，由球的性质可知，
易得，则，此时无解．
当O在线段的延长线上时，由球的性质可知，
，解得，所以，
所以球O的表面积，
故选：D．
【点睛】求解外接球问题的关键在于确定球心的位置，而确定球心位置的依据一是球心到球面上各点的距离都等于球的半径，二是球心与截面圆圆心的连线垂直于截面．由此出发，利用一些特殊模型，或借助一般方法，即可确定外接球球心的位置．
3．（2023·浙江温州·乐清市知临中学校考二模）如今中国被誉为基建狂魔，可谓是逢山开路，遇水架桥.公路里程､高铁里程双双都是世界第一.建设过程中研制出用于基建的大型龙门吊､平衡盾构机等国之重器更是世界领先.如图是某重器上一零件结构模型，中间最大球为正四面体的内切球，中等球与最大球和正四面体三个面均相切，最小球与中等球和正四面体三个面均相切，已知正四面体棱长为，则模型中九个球的表面积和为（ ）
A．B．C．D．
【答案】B
【分析】作出辅助线，先求出正四面体的内切球半径，再利用三个球的半径之间的关系得到另外两个球的半径，得到答案.
【详解】如图，取的中点，连接，，则，，
过点作⊥底面，垂足在上，且，
所以，故，
点为最大球的球心，连接并延长，交于点，则⊥，
设最大球的半径为，则，
因为∽，所以，即，解得，
即，则，故
设最小球的球心为，中间球的球心为，则两球均与直线相切，设切点分别为，
连接，则分别为最小球和中间球的半径，长度分别设为，
则，则，
又，所以，解得，
又，故，解得，
所以，
模型中九个球的表面积和为.
故选：B
【点睛】解决与球有关的内切或外接的问题时，解题的关键是确定球心的位置．对于外切的问题要注意球心到各个面的距离相等且都为球半径；对于球的内接几何体的问题，注意球心到各个顶点的距离相等，解题时要构造出由球心到截面圆的垂线段、小圆的半径和球半径组成的直角三角形，利用勾股定理求得球的半径
考点八、最值与球体综合
1．（2023·云南·统考模拟预测），，，在同一个球面上，是边长为6的等边三角形；三棱锥的体积最大值为，则三棱锥的外接球的体积为（ ）
A．B．C．D．
【答案】B
【分析】由图可得三棱锥的高，进而由直角三角形，可求出外接圆半径，即可求出结果.
【详解】
如图，三角形ABC的中心为M，球心为O，当时，三棱锥体积最大，，设，
则
外接圆体积为
故选：B
2．（2023·广东茂名·统考一模）已知菱形ABCD的各边长为2，.将沿AC折起，折起后记点B为P，连接PD，得到三棱锥，如图所示，当三棱锥的表面积最大时，三棱锥的外接球体积为（ ）
A．B．C．D．
【答案】D
【分析】根据题意结合三角形面积公式分析可得当时，三棱锥的表面积取最大值，再根据直角三角形的性质分析三棱锥的外接球的球心和半径，即可得结果.
【详解】由题意可得：均为边长为2的等边三角形，为全等的等腰三角形，
则三棱锥的表面积，
当且仅当，即时，三棱锥的表面积取最大值，
此时为直角三角形，，
取的中点，连接，由直角三角形的性质可得：，
即三棱锥的外接球的球心为，半径为，故外接球体积为.
故选：D.
【点睛】结论点睛：若三棱锥有两个面为共斜边的直角三角形，则三棱锥的外接球的球心为该斜边的中点.
3．（2023·湖北黄冈·浠水县第一中学校考模拟预测）某正六棱锥外接球的表面积为，且外接球的球心在正六棱锥内部或底面上，底面正六边形边长，则其体积的取值范围是（ ）
A．B．
C．D．
【答案】C
【分析】根据正六棱锥和球的几何性质，结合球的表面积公式、棱锥的体积公式、导数的性质进行求解即可.
【详解】设该正六棱锥的高，侧棱长为，设该正六棱锥外接球的半径为，如图，
因为正六棱锥外接球的表面积为，
所以有，
因为外接球的球心在正六棱锥内部或底面上，所以，
设，在正六边形中，因为正六边形边长为，所以，
在中，由余弦定理可知，
在直角三角形中，，
所以有，
由勾股定理可知，
因为，所以，
因此有4，而，所以，
该正六棱锥的体积，
，当时，单调递增，
所以，，
因此该正六棱锥的体积的取值范围是，
故选：C
4．（2023·河南·校联考模拟预测）已知四棱锥的底面是矩形，.若四棱锥的外接球的体积为，设是该球上的一动点，则三棱锥体积的最大值为（ ）
A．B．C．D．
【答案】D
【分析】易得四边形ABCD和三角形PAD的外接圆的圆心，分别再作垂线从而得到外接球的球心，再由为直角三角形，得到其外接圆直径PB，再结合外接球的半径求得球心到面PAB的距离,再加上外接球的半径，得到M到面PAB的最大值距离求解.
【详解】解：如图，

在矩形中，连接对角线，记，则点为矩形的外接圆圆心，
设，
在中，由余弦定理得，
即，的外接圆半径为.
记的外接圆圆心为，则，取的中点，连接，显然，，且共线，
因为，
所以平面，即平面，平面，有，而平面，
所以平面.
过作平面，使，连接，于是，则四边形为矩形，
有，则平面，
根据球的性质，得点为四棱锥外接球的球心，
因为球的体积为，
所以，解得，
而，在中，，
所以外接圆直径.
取的中点，连接，显然为外接圆圆心，则平面，且，
所以四棱锥的外接球上的点到平面的距离的最大值为8，即三棱锥的高的最大值为8，
而，
故三棱锥的体积的最大值为.
故选：D.
5．（2023·河南·校联考模拟预测）点是圆柱上底面圆周上一动点，是圆柱下底面圆的内接三角形，已知在中，内角、、的对边分别为、、，若，，三棱锥的体积最大值为，则该三棱锥外接球的表面积为（ ）
A．B．C．D．
【答案】B
【分析】利用余弦定理结合基本不等式可求得面积的最大值，利用正弦定理可求得圆柱底面圆半径，利用锥体体积公式可求得圆柱的高，进而可求得该三棱锥外接球的半径，结合球体表面积公式可求得结果.
【详解】在中，由余弦定理可得，
即，当且仅当时，等号成立，
所以，，
设圆柱的高为，则，

因为三棱锥的体积的最大值为，则，所以，，
圆柱底面圆半径，
设三棱锥的外接球的半径为，则该三棱锥的外接球和圆柱的外接球为同一个球，
则，因此，三棱锥外接球的表面积为.
故选：B.
6．（2023·全国·模拟预测）如图，在三棱锥中，平面，，，，，，，分别为，，，的中点，为上一点，，当的面积取得最小值时，三棱锥外接球的表面积为（ ）
A．B．C．D．
【答案】B
【分析】连接，，根据中位线性质得到线线平行关系，再利用线面垂直的性质得到线线垂直，设，，根据得到，得到，再根据基本不等式即可求出最值，再转化为长方体外接球问题即可.
【详解】连接，，因为，，，分别为，，，的中点，
所以，，，
则，因为平面，
所以平面，平面，
平面，所以，所以，
平面，所以．
设，，则，，，
因为，所以，即，
整理得，
所以．
由基本不等式得，
当且仅当，即，时等号成立，
所以当取得最小值时，，．
因为，平面，
所以可将三棱锥补形为如图所示的长方体，
则三棱锥的外接球即该长方体的外接球，
易知该长方体外接球的直径为，
故三棱锥外接球的半径为，
故三棱锥外接球的表面积为，
故选：B．
【点睛】方法点睛：求解有关三棱锥外接球的问题时，常见方法有两种：一种是补形，解题时要认真分析图形，看能否把三棱锥补形成一个正方体（长方体），若能，则正方体（长方体）的顶点均在外接球的球面上，正方体（长方体）的体对角线为外接球的直径；另一种是直接法，三棱锥中过任意两个面的外接圆圆心的垂线的交点即三棱锥外接球的球心．
1．（2023·河南开封·统考三模）在三棱锥中，，平面ABC，，，则三棱锥外接球体积的最小值为（ ）
A．B．C．D．
【答案】A
【分析】将三棱锥可以补成长方体，从而得到为三棱锥的外接球的直径，要想体积最小，则最小即可，设，表达出，从而得到，进而求出外接球体积的最小值.
【详解】根据题意三棱锥可以补成分别以为长、宽、高的长方体，其中为长方体的对角线，
则三棱锥的外接球球心即为的中点，要使三棱锥的外接球的体积最小，则最小．
设，则，，，
所以当时，，则有三棱锥的外接球的球半径最小为，
所以．
故选：A
2．（2023·广东佛山·华南师大附中南海实验高中校考模拟预测）如图，球的表面积为，四面体内接于球，是边长为的正三角形，平面平面，则该四面体体积的最大值为（ ）
A．B．C．D．
【答案】B
【分析】首先根据球的表面积求得求得半径，再根据题意得出当时，点到底面的距离最大，求出点到底面的距离即可求出最大值.
【详解】因为球的表面积为，所以，
由题意知底面三角形的面积为定值，要使四面体体积的最大，只须顶点到底面的距离最大即可，
又因为平面平面，可知当时，点到底面的距离最大，
外接圆的半径，则到面的距离为，且到面的距离为，
设点到平面的距离为，则，解得，
此时体积最大值为.
故选：B.
3．（2023·福建厦门·统考模拟预测）一封闭圆台上、下底面半径分别为1，4，母线长为6.该圆台内有一个球，则这个球表面积的最大值是（ ）
A．B．C．D．
【答案】A
【分析】根据题意，作出圆台轴截面，分析可知，当球与相切时，其表面积最大，再结合条件求得球的半径，即可得到结果.
【详解】
画出圆台的轴截面，要使球的表面积最大，则球需要与相切，
设圆的半径为，则，
又因为，所以，
因为，作，，
所以，所以，
所以，
且，即,
解得，
所以球表面积的最大值为，
故选:A
4．（2023·西藏林芝·统考二模）在三棱锥中，，平面经过的中点E，并且与BC垂直，当α截此三棱锥所得的截面面积最大时，此时三棱锥的外接球的表面积为（ ）
A．B．C．D．
【答案】D
【分析】取靠近的四等分点，的中点，截此三棱锥所得的截面为平面，当时截面面积最大，，为，外接圆圆心，球心满足面，面，由求得外接球的半径进而求得球的表面积.
【详解】
如图所示，取中点及靠近的四等分点，的中点，连接，，，，，
由，所以，又是中点，是的中点，所以
可知，同理可得，
又，平面，平面，所以平面，所以平面即为平面，
又因为，所以，所以，
所以截此三棱锥所得的截面面积为，
当时，取得最大值，
设外接球球心为，半径为，，分别为，外接圆圆心，球心满足面，面，
又因为和均为边长为4的正三角形，所以，
所以四边形为正方形，且，又,所以，
∴.
故选：D.
5．（2023·河南·校联考模拟预测）在三棱锥中，平面，且，当三棱锥的体积取最大值时，该三棱锥外接球的体积是（ ）
A．B．C．D．
【答案】B
【分析】设，则三棱锥的体，构造函数，利用导数求最值可得，再求三棱锥外接球半径可得答案．
【详解】设，则，故三棱锥的体积，
设，则，
由，得，由，得，则在上单调递增，
在上单调递减，从而，
即三棱锥体积的最大值是，此时，即，
因为平面，把三棱锥不成一个长方体，则三棱锥与所补成的长方体有相同的外接球，
所以外接球的半径，则三棱锥外接球的体积为．
故选：B.

6．（2023·辽宁·校联考三模）在三棱锥中，，平面经过的中点，并且与垂直，当截此三棱锥所得的截面面积最大时，此时三棱锥的外接球的表面积为（ ）
A．B．C．D．
【答案】D
【分析】取靠近的四等分点，的中点，截此三棱锥所得的截面为平面，当时截面面积最大，，为，外接圆圆心，球心满足面，面，由求得外接球的半径进而求得球的表面积.
【详解】
如图所示取靠近的四等分点，的中点，连接，，.
由，可知.同理可知.
又，所以平面，所以平面即为平面.
又易知，
所以截此三棱锥所得的截面面积为，
当时，取得最大值，
设为外接球球心，，为，外接圆圆心，球心满足面，面，
所以四边形为正方形，且，，，
∴.
故选：D.
考点九、内切球综合
1．（2023·山东泰安·统考模拟预测）将半径为，圆心角为的扇形围成一个圆锥（接缝处忽略不计），则该圆锥的内切球的表面积为（ ）
A．B．C．D．
【答案】C
【分析】先算出扇形的弧长，从而可得圆锥底面的半径，故可求轴截面内切圆的半径即为圆锥内切球的半径，最后根据公式可求体积.
【详解】
设圆锥的母线长为，底面半径为，由题意可得，由，所以．
因为，圆锥的轴截面是边长为的等边三角形，
该等边三角形（如图）的内切圆半径为圆锥内切球半径，
而等边三角形的边长为4，故，故．
故选：C．
2．（2023·浙江台州·统考模拟预测）在四棱锥中，平面平面，为边长为1的等边三角形，底面为矩形.若四棱锥存在一个内切球（内切球定义：若一个多面体的各面都与一个球的球面相切，则称这个球是这个多面体的内切球），则内切球的表面积为（ ）
A．B．C．D．
【答案】D
【分析】根据内切球在等边三角形内的“正投影”求得内切球的半径，进而求得内切球的表面积.
【详解】由于平面平面，为边长为1的等边三角形，底面为矩形，
所以四棱锥的内切球在等边三角形的“正投影”是等边三角形的内切圆，
设等边三角形的内切圆半径为，
则，解得，
所以内切球的半径为，其表面积为.
故选：D
3．（2023秋·浙江杭州·高三浙江省桐庐中学期末）已知四面体，且，，面面，则四面体的外接球与内切球的表面积之比为（ ）
A．B．C．D．
【答案】C
【分析】取中点，中点，以为轴建立坐标系，利用外接球球心到顶点的距离相等求外接球半径，利用等体积法求内切球半径即可求解.
【详解】取中点，中点，连接，
因为，则，又且，则，
又面面，面面，面，所以面，
由面，则，
所以两两垂直，以为轴建立如图所示坐标系，
则，，，，
设四面体外接球球心为，因为△外接圆圆心为，所以面，
设，因为，所以解得，
即，所以四面体外接球半径，
因为，，
所以，即，△为等腰三角形，
所以△在边上的高为，
所以四面体的侧面积
，
四面体的体积，
设四面体内切球的半径为，
则由等体积法可得解得，
所以四面体的外接球与内切球的表面积之比为，
故选：C
4．（2023秋·浙江丽水·高三浙江省丽水中学校联考期末）将菱形沿对角线折起，当四面体体积最大时，它的内切球和外接球表面积之比为（ ）
A．B．C．D．
【答案】C
【分析】当平面平面时，四面体的高最大，并利用导函数讨论体积的最大值，构造长方体求外接球的半径，利用等体积法求内切球的半径，进而可求解.
【详解】不妨设菱形的边长为，，，
外接球半径为，内切球半径为，
取中点为，连接，
因为，所以，
当平面平面时，平面平面，
平面，所以平面，
此时四面体的高最大为，
因为，所以
所以，
，
令解得，
令解得，
所以在单调递增，单调递减，
所以当时最大，最大体积为，
此时，
以四面体的顶点构造长方体，长宽高为，
则有解得，所以，
所以外接球的表面积为，
又因为，
所以，
，
所以，
所以，
所以，所以内切球的表面积为，
所以内切球和外接球表面积之比为，
故选:C.
5．（2023·广东·统考模拟预测）已知某圆锥的内切球（球与圆锥侧面､底面均相切）的体积为，则该圆锥的表面积的最小值为（ ）
A．B．C．D．
【答案】A
【分析】先求得内切球半径，再画图设底面半径为，利用三角函数值代换表达出表面积的公式，再设，根据基本不等式求最小值即可
【详解】设圆锥的内切球半径为，则，解得，设圆锥顶点为，底面圆周上一点为，底面圆心为，内切球球心为，内切球切母线于，底面半径，，则，又，故，又，故，故该圆锥的表面积为，令，则，当且仅当，即时取等号.
故选：A.
6．（2023秋·江苏常州·高三常州高级中学校考开学考试）将一个半径为的球削成一个体积最大的圆锥，则该圆锥的内切球的半径为（ ）
A．B．C．D．
【答案】D
【分析】设圆锥的底面半径为，则高为，表示出圆锥的体积，换元后利用导数可求出体积的最大值，从而可求出圆锥的底面半径和高，再求出母线长，作出圆锥的截面，然后利用三角形相似可求出圆锥内切球的半径.
【详解】设圆锥的底面半径为，则高为，
所以圆锥的体积为，
令，得，
所以，
则，
所以当时，，当时，，
所以在上递增，在上递减，
所以当时，取得最大值，即时，圆锥的体积最大，
此时圆锥的高为，母线长为，
设圆锥的内切球半径为，圆锥的轴截面图如图所示，则
，
因为，
所以，所以,
即，解得，
故选：D

【点睛】关键点点睛：此题考查圆锥的内切球问题，考查导数的应用，解题的关键是表示出圆锥的体积，化简后利用导数求出其最大值，从而可确定圆锥的大小，考查空间想象能力和计算能力，属于难题.
1．（2023·浙江宁波·镇海中学校考模拟预测）表面积为的球内切于圆锥，则该圆锥的表面积的最小值为（ ）
A．B．C．D．
【答案】B
【分析】求出圆锥内切球的半径，设圆锥顶点为，底面圆周上一点为，底面圆心为，内切球球心为，内切球切母线于，底面半径，，则，求出，再换元利用基本不等式求出函数的最小值得解.
【详解】设圆锥的内切球半径为，则，解得，
设圆锥顶点为，底面圆周上一点为，底面圆心为，内切球球心为，
轴截面如下图示，内切球切母线于，底面半径，，则，
又，故，
又，故，
故该圆锥的表面积为，
令，所以，
所以.
（当且仅当时等号成立）
所以该圆锥的表面积的最小值为.
故选：B

2．（2023春·河北衡水·高三河北衡水中学校考阶段练习）《九章算术》是我国古代数学名著，它在几何学中的研究比西方早一千多年，其中有很多对几何体外接球与内切球的研究．其中的一些研究思想启发着后来者的研究方向．已知正四棱锥的外接球半烃为R，内切球半径为r，且两球球心重合，则（ ）
A．2B．C．D．
【答案】B
【分析】正四棱锥的外接球和内接球球心重合，说明其结构特殊，找出结构的特殊性，再计算.
【详解】如图：
设底面正方形ABCD的对角线长为2a，高为h，，正方形的中心为O，外接球的球心为，
则有即，在 中， ① ，②，
以O为原点，建立空间直角坐标系如上图，
则有 ， ，
设平面PCD的一个法向量为 ，则有 ， ，
令 ，则 ，
设向量 与平面PCD的夹角为 ，则 ，
球心 到平面PCD的距离 ，
，由①得即③，
故设，则③可整理成 ，两边平方得 ， ，
由①②得 ；
故选：B.
3．（2023·河北秦皇岛·校联考模拟预测）如图，该几何体为两个底面半径为1，高为1的相同的圆锥形成的组合体，设它的体积为，它的内切球的体积为，则（ ）

A．B．
C．D．
【答案】D
【分析】轴截面四边形的内切圆的半径即为该几何体内切球的半径，求出半径，再根据球的体积公式和圆锥的体积公式即可得解.
【详解】如图，四边形为该几何体的轴截面，
则四边形的内切圆的半径即为该几何体内切球的半径，
设内切球的半径为，
由，得，
则，
，
所以.
故选：D.

4．（2023·湖南·校联考模拟预测）定义：与圆锥的底面和各母线均相切的球，称为圆锥的内切球，此圆锥称为球的外切圆锥．已知某圆锥的内切球半径等于1，则该圆锥体积的最小值为（ ）
A．B．C．D．
【答案】C
【分析】圆锥的内切球问题，作图分析利用基本不等式求解即可.
【详解】如图，作出该几何体的轴截面得到如图所示的平面图形，

设该圆锥的内切球球心为，底面圆的圆心为点，
底面半径为，高为，
法一：由等面积法可得：，
化简得：，
又：，
∴，当且仅当，即时取等号．
法二：如图：，∴，
∴，∵，∴，
∴，
当且仅当，即时取等号．
故选：C．
5．（2023·湖北·统考二模）已知直三棱柱存在内切球，若，则该三棱柱外接球的表面积为（ ）
A．B．C．D．
【答案】D
【分析】求出直三棱柱的高后可求其外接球的半径，从而可求外接球的表面积.
【详解】因为，故，
故的内切圆的半径为.
因为直三棱柱存在内切球，故直三棱柱的高即为内切球的直径.
而内切球的半径即为底面三角形内切圆的半径，故内切球的半径为1，
故直三棱柱的高为2.
将直三棱柱补成如图所示的长方体，则外接球的直径即为该长方体的体对角线，
故外接球的半径为，
故外接球的的表面积为.
故选：D.
6．（2023·福建宁德·校考模拟预测）将一个半径为2的球削成一个体积最大的圆锥，则该圆锥的内切球的半径为（ ）
A．B．
C．D．
【答案】D
【分析】设圆锥的底面半径为，则圆锥的高为，表示出圆锥的体积，换元后利用导数可求出体积的最大值，从而可求出圆锥的底面半径和高，再求出母线长，作出圆锥的截面，然后利用三角形相似可求出圆锥内切圆的半径.
【详解】设圆锥的底面半径为，则圆锥的高为，
所以圆锥的体积，
令（），则，
所以，
则，
当时，，当时，，
所以在上递增，在上递减，
所以当，即时，圆锥的体积最大，此时圆锥的高为，母线长为，
设圆锥的内切球半径为，圆锥的截面如图所示,
则，，，
因为∽，所以，，解得,
故选：D
【点睛】关键点点睛：此题考查圆锥的内切球问题，解题的关键是表示出圆锥的体积，化简后利用导数求出其最大值，从而可确定出圆的大小，考查空间想象能力和计算能力，属于较难题.
考点十、球心不确定类型
1．（2023·江西南昌·南昌市八一中学校考三模）已知四棱锥的底面是矩形，高为，，，，，则四棱锥的外接球的表面积为（ ）
A．B．C．D．
【答案】C
【分析】作出辅助线，求出平面外接圆半径，再利用勾股定理求出外接球的半径，即可求出球的表面积.
【详解】如图，在矩形中，连接对角线，记，则点为矩形的外接圆圆心，
取的中点，连接，记的外接圆圆心为，易知，且共线.
因为，平面，所以平面，
所以平面，平面，，，平面，
所以平面，所以，所以，易得，
所以由正弦定理得的外接圆半径为，即.
过作平面，且，连接，由平面，
可知，则四边形为矩形，所以，则平面.
根据球的性质，可得点为四棱锥的外接球的球心，
因为，所以四棱锥的外接球的表面积为.

故选：C
2．（2023·甘肃·模拟预测）如图，在菱形中，，，E为对角线BD的中点，将沿BD折起到的位置，若，则三棱锥的外接球的表面积为（ ）
A． B．C．D．
【答案】A
【分析】过球心作平面，则为等边三角形的中心，由与都是边长相同的等边三角形得，利用勾股定理得、，最后由球的的表面积公式计算可得答案.
【详解】过球心作平面，则为等边三角形的中心，∵四边形是菱形，，∴与都是边长相同的等边三角形，
∵，∴，∵，
∴，∴，，中，，
由勾股定理得，
∴球的半径，
∴三棱锥的外接球的表面积为.
故选：A．
【点睛】方法点睛：一般外接球需要求球心和半径，首先应确定球心的位置，借助于外接球的性质，球心到各顶点距离相等，这样可先确定几何体中部分点组成的多边形的外接圆的圆心，过圆心且垂直于多边形所在平面的直线上任一点到多边形的顶点的距离相等，然后同样的方法找到另一个多边形的各顶点距离相等的直线（这两个多边形需有公共点），这样两条直线的交点，就是其外接球的球心，再根据半径，顶点到底面中心的距离，球心到底面中心的距离，构成勾股定理求解，有时也可利用补体法得到半径.
3．（2023·陕西咸阳·武功县普集高级中学校考模拟预测）如图，在正三棱台中，，，，则正三棱台的外接球表面积为（ ）

A．64B．C．D．
【答案】B
【分析】先求得台体的高，然后利用勾股定理列方程，求得外接球的半径，进而求得外接球的表面积.
【详解】设外接球球心为，等边三角形的外心为，等边三角形的外心为，
三点共线，则是正三棱台的高，
设台体的高为，设外接球的半径为，
过作，垂足为，根据正棱台的性质可知，
所以平面，平面，所以，
设等边三角形的外接圆半径为，由正弦定理得.
设等边三角形的外接圆半径为，由正弦定理得.
在直角三角形中，，
所以.
当球心O在线段上，则，解得，
当球心O在的延长线上时，则，无解，
所以正三棱台的外接球表面积为.

故选：B
4．（2023·河北秦皇岛·校联考二模）已知正方体的棱长为2，P，Q分别是，的中点，则经过点，Q，C，D，C1的球的表面积为（ ）
A．B．C．D．
【答案】D
【分析】分别求出的外接圆半径，矩形的外接圆半径，再利用几何关系求出球的半径，进而求出结果.
【详解】
根据正方体，得，，所以平面，
四边形是矩形，其中，，
的三边为，
，，
，
设的外接圆半径为，则，
于是，
设矩形的外接圆半径为，则，
设球心为，过作平面，垂足为，
过作平面，垂足为，
则是矩形的外心，是三角形的外心，
取中点，则，
于是平面，
所以四边形是矩形.
设球半径为，，
则，
于是球的表面积为.
故选：D.
1．（2023·四川·四川省金堂中学校校联考三模）如图，在梯形中，，将沿对角线折起，使得点翻折到点，若面面，则三棱锥的外接球表面积为（ ）
A．B．C．D．
【答案】B
【分析】设为的中点，为的中点，为的外心，为三棱锥的外接球球心，利用球的截面性质得到四边形为矩形，然后设外接球半径为，由求解.
【详解】解：如图，
设为的中点，为的中点，为的外心，为三棱锥的外接球球心，
则面面.
由题意得为的外心，
在中，，
所以，
又四边形为矩形，
，设外接球半径为，
则外接球表面积，
故选：B.
2．（2023·江西·校联考模拟预测）已知三棱锥满足，．则其外接球的体积为（ ）
A．B．C．D．
【答案】C
【分析】利用正弦定理求得外接圆半径，根据三棱锥图像，分别表示出，，然后利用勾股定理，解得，进而利用球体的体积公式即可得出答案.
【详解】在中，，，
根据三角形的外接圆半径公式，
可得的外接圆半径，
如图所示．
设点在平面内的投影的为，则，
在中，
因为，解得，
设三棱锥的外接球半径，
即，，
在中，由勾股定理得，
即，解得，
故三棱锥的外接球半径，
根据球体的体积公式.
故选：C
3．（2023·全国·校联考模拟预测）在正三棱锥P-ABC中，D，E分别为侧棱PB，PC的中点，若，且，则三棱锥P-ABC外接球的表面积为（ ）
A．B．C．D．
【答案】C
【分析】结合题意，利用三角形相似得到，取线段PE的中点F，连接DF，AF，利用余弦定理和勾股定理求出外接球半径，代入外接球的表面积公式即可求解.
【详解】如图，因为P-ABC为正三棱锥，所以，．
取线段PE的中点F，连接DF，AF，因为D为PB的中点，所以，．因为AD⊥BE，所以．在中，，
由勾股定理，得．设，PA=x，
在中，由余弦定理的推论，得①．
同理，在中，由余弦定理的推论，得②．
联立①②，解得，．
在中，由余弦定理，得，所以．取的中心，连接，，则平面ABC，
三棱锥P-ABC的外接球球心O在上，连接OA，设外接球半径为R．
在中，OA=R，，
所以，
所以，所以，
即，解得，
所以所求外接球的表面积为．
故选：C．
4．（2023·河北邯郸·统考三模）三棱锥中，平面，，．过点分别作，交于点，记三棱锥的外接球表面积为，三棱锥的外接球表面积为，则（ ）
A．B．C．D．
【答案】B
【分析】取的中点，的中点，连，，，，证明是三棱锥的外接球的球心，为该球的直径；是三棱锥的外接球的球心，为该球的直径，设，求出，根据球的表面积公式可求出结果.
【详解】取的中点，的中点，连，，，，
因为平面，平面，所以，，，
因为，，平面，所以平面，
因为平面，所以，
在直角三角形中，是斜边的中点，所以，
在直角三角形中，是斜边的中点，所以，
所以是三棱锥的外接球的球心，为该球的直径.
因为，是斜边的中点，所以，
因为， 是斜边的中点，所以，
所以是三棱锥的外接球的球心，为该球的直径.
设，则，
则，，
所以.
故选：B.
考点十一、球体多选题综合
1．（2023·湖南·湖南师大附中校联考模拟预测）如图，正方体的棱长为3，点是侧面上的一个动点（含边界），点在棱上，且，则下列结论正确的有（ ）
A．沿正方体的表面从点到点的最短路程为
B．保持与垂直时，点的运动轨迹长度为
C．若保持，则点的运动轨迹长度为
D．当在点时，三棱锥的外接球表面积为
【答案】BCD
【分析】根据平面展开即可判断A；过做平面平面，即可判断B；根据点的轨迹是圆弧，即可判断C；建立空间直角坐标系求得圆心坐标即可判断D.
【详解】对于，将正方体的下面和侧面展开可得如图图形，
连接，则，故错误；
对于，因为平面，平面，，又，平面，
所以平面，平面，
所以，同理可得，平面，
所以平面，
所以过点作交交于，过作交交于，
由，可得，平面，平面，
所以平面，同理可得平面，，
则平面平面，
设平面交平面于，则的运动轨迹为线段，
由点在棱上，且，可得，
所以，故B正确；
对于，若，则在以为球心，为半径的球面上，
过点作平面，则，此时，
所以点在以为圆心，2为半径的圆弧上，此时圆心角为，
点的运动轨迹长度为，故正确；
对于D，以为坐标原点，所在直线分别为轴建系，
则，设三棱锥的外接球球心为，由得，
，
解得：，
所以三棱锥的外接球半径，
所以三棱锥的外接球表面积为，D正确.
故选：BCD.
2．（2023·云南昭通·统考模拟预测）如图，已知正方体的棱长为2，点是的中点，点是线段上的一动点，则下列说法正确的是（ ）
A．
B．三棱锥的内切球的体积为
C．三棱锥的体积为
D．直线与平面所成角的最大值为
【答案】ACD
【分析】建立空间坐标系，利用向量与垂直判断A，利用体积分割法求解内切球的半径，进一步求内切球的体积判断B，证明平面，根据等体积法计算棱锥的体积判断C，利用向量法计算直线与平面所成角的正弦值，求函数最值即可求出最大角判断D.
【详解】由正方体性质知，如图
以点A为坐标原点，AB、AD、分别为x、y、z轴，建立空间直角坐标系.
则，，，，，，，，，因为点是线段上的一动点，所以设，则.
对于A，因为，，所以，
所以，故，故选项A正确；
对于B，三棱锥的体积为，
又三棱锥的所有棱长均为，
所以三棱锥的表面积为，
设三棱锥的内切球半径为，则，
解得，所以三棱锥的内切球的体积为，故选项B错误；
对于C，
设，连接BF，因为，且，所以四边形为平行四边形，所以，又平面，平面，所以平面，所以点P到平面的距离为点到平面的距离，所以，故选项C正确；
对于D，易知平面的一个法向量为，，设直线与平面所成角为，则，令，因为，所以，
则，
所以即时，有最大值为，又，且函数在上单调递增，
所以的最大值为，即直线与平面所成角的最大值为，故选项D正确.
综上，说法正确的是ACD.
故选：ACD
6．（2023·辽宁辽阳·统考二模）正三棱锥的底面边长为3，高为，则下列结论正确的是（ ）
A．
B．三棱锥的表面积为
C．三棱锥的外接球的表面积为
D．三棱锥的内切球的表面积为
【答案】ABD
【分析】求得的位置关系判断选项A；求得三棱锥的表面积判断选项B；求得三棱锥的外接球的表面积判断选项C；求得三棱锥的内切球的表面积判断选项D.
【详解】如图，
取棱的中点，连接
则正三棱锥中，.
因为平面，且，
所以平面，则，故A正确；
作平面，垂足为，则.
由正三棱锥的性质可知在上，且.
因为，所以，则.
因为，所以，
则三棱锥的表面积，故B正确；
设三棱锥的外接球的球心为，半径为，则在上，
连接，则，
即，解得，
则三棱锥的外接球的表面积为，故C错误.
设三棱锥的内切球的半径为，
则，
解得，从而三棱锥的内切球的表面积
为，故D正确.
故选：ABD
7．（2023·安徽·合肥一中校联考模拟预测）已知半径为R的球与圆台的上下底面和侧面都相切.若圆台上下底面半径分别为r1和r2，母线长为l，球的表面积与体积分别为S1和V1，圆台的表面积与体积分别为S2和V2.则下列说法正确的是（ ）
A．B．
C．D．的最大值为
【答案】ABC
【分析】根据题意结合圆台与球的表面积、体积公式逐项分析判断.
【详解】由切线长定理易得，A正确；
由勾股定理知，解得，B正确；
因为，
，
所以正确；
因为，当且仅当时，等号成立，
这与圆台的定义矛盾，故D错误.
故选：ABC.
1．（2023·山东烟台·校联考三模）底面为直角三角形的三棱锥的体积为4，该三棱锥的各个顶点都在球O的表面上，点P在底面ABC上的射影为K，，则下列说法正确的是（ ）
A．若点K与点A重合，则球O的表面积的最小值为
B．若点K与点A重合，则球O的体积的最小值为
C．若点K是的斜边的中点，则球O的表面积的最小值为
D．若点K是的斜边的中点，则球O的体积的最小值为
【答案】AD
【分析】设的两直角边长分别为x，y，根据题意求得，然后分点K与点A重合和点K是的斜边的中点两种情况进行求解即可判断.
【详解】设的两直角边长分别为x，y，球O的半径为R.因为三棱锥的体积为4，，所以，解得.
对于选项A，B：由题意知平面ABC，所以（当且仅当时取等号），解得，
所以球O的表面积，球O的体积，故A正确，B错误；
对于选项C，D：若点K是的斜边的中点，则，（球O的球心位于直线PK上）
所以（当且仅当时取等号），即，
所以球O的表面积，球O的体积，故C错误，D正确.
故选：AD
【点睛】方法技巧
求解此类题要过好三关：一是构造关，即会构造长方体模型快速求解外接球的直径，长方体的外接球的直径等于共点的三条棱长的平方和的开方；二是方程关，即会利用三棱锥的底面三角形的外接圆的圆心､球心与三棱锥的顶点构成的直角三角形，用勾股定理得关于球半径的方程；三是最值关，利用基本不等式求最值，要注意“一正二定三相等”.
2．（2023·湖南长沙·长沙一中校考一模）如图圆柱内有一个内切球，这个球的直径恰好与圆柱的高相等，为圆柱上下底面的圆心，为球心，为底面圆的一条直径，若球的半径，则下列各选项正确的是（ ）
A．球与圆柱的体积之比为
B．四面体的体积的取值范围为
C．平面截得球的截面面积最小值为
D．若为球面和圆柱侧面的交线上一点，则的取值范围为
【答案】ABD
【分析】根据给定的条件，利用球、圆柱的体积公式计算判断A；利用建立函数关系判断B；求出球心O到平面DEF距离的最大值判断C；令点P在圆柱下底面圆所在平面上的投影点为Q，设，利用勾股定理建立函数关系，求出值域可判断D.
【详解】对于A，球的体积为，圆柱的体积，则球与圆柱的体积之比为，A正确；
对于B，设为点到平面的距离，，而平面经过线段的中点，
四面体CDEF的体积，
所以四面体的体积的取值范围为，B正确；
对于C，过作于，如图，而，则，
又，于是，设截面圆的半径为，球心到平面的距离为，则，
又，则平面DEF截球的截面圆面积，C错误；
对于D，令经过点P的圆柱的母线与下底面圆的公共点为Q，连接，
当与都不重合时，设，则，当与之一重合时，上式也成立，
因此，，
则，
令，则，而，即，
因此，解得，所以的取值范围为，D正确.
故选：ABD.
3．（2023·广东深圳·深圳中学校考模拟预测）如图，棱长为2的正四面体中，，分别为棱，的中点，为线段的中点，球的表面与线段相切于点，则下列结论中正确的是（ ）

A．平面
B．球的体积为
C．球被平面截得的截面面积为
D．球被正四面体表面截得的截面周长为
【答案】ABD
【分析】根据题中条件，根据线线垂直，证明线面垂直，可判断球为正四面体的棱切球，可判断BCD.
【详解】
设､分别为､的中点，连接，，，，，，，
则，，，，
故，，则四边形为平行四边形.
故，交于一点，且互相平分，即点也为的中点，
又，，故，.
，，平面，故平面，
由于，平面，则平面，故，
结合点也为的中点，同理可证，
，，平面，
故平面，A正确；
由球的表面正好经过点，则球的半径为，棱长为2的正四面体中，
，为的中点，则，故，则，
所以球的体积为，B正确；
由平面，平面，故平面平面，
平面平面，由于平面，
延长交平面于点，
则平面，垂足落在上，且为正的中心，
故，所以，
即为球心到平面的距离为
故球被平面截得的截面圆的半径为，
则球被平面截得的截面圆的面积为，C错误；
由A的分析可知，也为棱，中点连线的中点，
则球与每条棱都交于棱的中点，
结合C的分析可知，
球被正四面体的每个面截得的截面都为圆，且圆的半径都为，
故球被正四面体表面截得的截面周长为，D正确.
故选：ABD.
4．（2023·福建泉州·泉州五中校考模拟预测）如图，棱长为2的正四面体中，，分别为棱，的中点，为线段的中点，球的表面正好经过点，则下列结论中正确的是（ ）

A．平面
B．球的体积为
C．球被平面截得的截面面积为
D．过点与直线，所成角均为的直线可作4条
【答案】ABD
【分析】设分别为的中点，连接，根据线面垂直的判定定理可判断A；求出球的半径，计算球的体积，进而判断B；求出球O被平面截得的截面圆的半径，可求得截面面积，进而判断C；通过平移与补形法，通过角平分线的转化寻找平面进而找出直线，从而可判断D.
【详解】设分别为的中点，连接，

则,
故，则四边形为平行四边形，
故交于一点，且互相平分，即O点也为的中点，
又，故,
平面，故平面，
由于平面，则平面，
故，结合O点也为的中点，同理可证,
平面，故平面，A正确；
由球O的表面正好经过点M，则球O的半径为,
棱长为2的正四面体中，，M为的中点，
则，故,
则，所以球O的体积为，B正确；
由平面，平面，故平面平面，
平面平面，由于平面，
延长交平面于G点，则平面，垂足G落在上，
且G为正的中心，故，
所以，
故球O被平面截得的截面圆的半径为，
则球O被平面截得的截面圆的面积为，C错误；
由题意得，正四面体可以放入正方体内，如下图所示，将平移至正方体的底面内，过
和的角平分线作垂直于底面的平面，即平面，在平面内一定存在过O点的两条直线使得该直线与直线，所成角均为，同理可知，过和的角平分线作垂直于底面的平面也存在两条直线满足题意，所以过点与直线，所成角均为的直线可作4条，D正确.

故选：ABD
【点睛】思路点睛：本题考查立体几何的综合问题.要结合图形的特点，作出适合的辅助线，要善于观察图形特点，放入特殊图形中从而快速求解.
【基础过关】
一、单选题
1．（2022·天津河西·天津市新华中学校考模拟预测）已知圆柱的底面直径和高都等于球的直径，则球与圆柱体积比是（ ）
A．B．C．D．
【答案】A
【分析】根据题意可知若球的半径为，则圆柱的底面半径为，高为，结合球与圆柱的体积公式计算即可得出结果.
【详解】设球的半径为，则圆柱的底面半径为，高为，
因为，
所以．
故选：A
2．（2022·天津和平·统考三模）已知某圆柱的轴截面为正方形，则此圆柱的表面积与此圆柱外接球的表面积之比为（ ）
A．B．C．D．
【答案】A
【分析】设出圆柱的底面半径，求解圆柱的高，球的半径，然后求解表面积的比．
【详解】解：圆柱的轴截面为正方形，其外接球为球，
设圆柱的底面半径为，则圆柱的高为，则球的半径，
所以圆柱的表面积为：；
球的表面积为，
则圆柱的表面积与球的表面积之比为．
故选：A．
3．（2022·天津南开·南开中学校考模拟预测）圆柱内有一个球，该球与圆柱的上、下底面及母线均相切，已知圆柱的体积为，则球的体积为（ ）
A．B．C．D．
【答案】A
【分析】设出球的半径为R，得到圆柱的底面圆的半径为R，高为2R，由圆柱体积列出方程，求出半径R，从而求出球的体积.
【详解】设球的半径为R，则圆柱的底面圆的半径为R，高为2R，
所以，解得：，
则球的体积为
故选：A
4．（2022·湖北黄冈·黄冈中学校考三模）若一个正六棱柱既有外接球又有内切球，则该正六棱柱的外接球和内切球的表面积的比值为（ ）
A．B．C．D．
【答案】C
【分析】正六棱柱有内切球，则到每个面的距离相等，即，可求内切球的半径，根据可求外接球的半径，代入球的面积公式计算．
【详解】如图：分别为底面中心，为的中点，为的中点
设正六棱柱的底面边长为
若正六棱柱有内切球，则，即内切球的半径
，即外接球的半径
则该正六棱柱的外接球和内切球的表面积的比值为
故选：C．
5．（2022·全国·模拟预测）在三棱锥中，点P在底面ABC的射影恰好落在BC的中点，，，，△PAB的面积为，则该三棱锥的外接球的表面积为（ ）
A．B．C．D．
【答案】C
【分析】根据题意△PAB的面积可得，在中根据勾股定理可得，结合球的性质可得,代入求解半径．
【详解】如图所示，取BC，AB的中点分别为，D，连接，PD，
设三棱锥的高，，外接球的半径为R，球心为O，
则根据题意△PAB的面积为，解得．
在中，，解得．
根据外接球的性质可知，，解得，
所以三棱锥的外接球O的表面积为，
故选：C．
6．（2022·全国·模拟预测）已知在三棱锥中，平面SBC，，，，则该三棱锥外接球体积为（ ）
A．B．C．D．
【答案】B
【分析】根据题意，将三棱锥补成以AC为侧棱的直棱柱，求解外接球的半径，利用球的体积公式求解即可.
【详解】如图，将三棱锥补成以AC为侧棱的直棱柱，设△BCS外接圆圆心为，半径为r，设△ADE外接圆圆心为，连接，，，取的中点O，则点O为三棱锥外接球球心，连接CO，设该三棱锥外接球半径为R，在△BCS中，，所以.在中，，所以该三棱锥外接球体积为，
故选：B.
二、填空题
7．（2023·全国·高三专题练习）已知三棱锥中， 面， 则三棱锥的外接球的体积为 .
【答案】
【分析】根据三棱锥的顶点是长方体的顶点即可求解.
【详解】
由题可知,该三棱锥在长方体中，且三棱锥的四个顶点为长方体的四个顶点，
所以三棱锥的外接球即为长方体的外接球，
由图可知长方体的长宽高分别为，
所以体对角线长，
所以外接球的体积等于.
故答案为:.
8．（2022·天津红桥·统考一模）一个长方体的各顶点均在同一球的球面上，且一个顶点上的三条棱的长分别为1、、3，则此球的体积为 ．
【答案】
【分析】求得长方体外接球的半径，从而求得球的体积.
【详解】长方体外接球的直径为，
所以外接球半径为，
所以球的体积为.
故答案为：
9．（2022·山西吕梁·统考三模）已知球的一个截面面积为，若球上的点到该截面的最大距离为3，则球的表面积为 ．
【答案】
【分析】设球的半径为，截面圆的半径为到截面的距离为，根据题设条件列方程组即可求解
【详解】设球的半径为，截面圆的半径为到截面的距离为，
则由题意得 解得
所以球的表面积为
故答案为：
10．（2022·吉林长春·长春吉大附中实验学校校考模拟预测）如图，在四棱锥中，底面为菱形，底面，，若，，则三棱锥的外接球表面积为 .
【答案】
【分析】根据三角形均为直角三角形，且面，可判断球心的位置为中点，进而根据几何关系可求半径.
【详解】∵平面，平面，∴，又，∴
取中点分别为,连接,
由于,平面,所以平面,
因为底面为菱形，所以，，且，所以,即是三角形外接圆的圆心，因此球心在直线上，
又,所以,因此可得为球心，
又，
∴.
故答案为：
【点睛】
【能力提升】
一、单选题
1．（2022·山东青岛·统考二模）《九章算术》中记录的“羡除”是算学和建筑学术语，指的是一段类似隧道形状的几何体，如图，羡除ABCDEF中，底面ABCD是正方形，平面ABCD，，其余棱长都为1，则这个几何体的外接球的体积为（ ）
A．B．C．D．
【答案】B
【分析】根据已知条件找出外接球的球心，求出半径，再利用球的体积公式即可求解.
【详解】连接,交于点,取的中点，则平面,,取的中点,连接,作,垂足为，如图所示
由题意可知，，所以,
所以,,所以,又,
所以，即这个几何体的外接球的球心为，半径为，
所以这个几何体的外接球的体积为.
故选：B.
2．（2022·江苏南京·模拟预测）已知，，，为球的球面上的四点，记的中点为，且，四棱锥体积的最大值为，则球的表面积为（ ）
A．B．C．D．
【答案】C
【分析】根据给定条件，确定四棱锥底面四边形形状，令，再建立r的函数，求出函数最大值作答.
【详解】因，则平面过球O的球心O，又的中点为，则点E是以AB为直径的球的截面小圆圆心，
连接，如图，则，四边形为梯形，令球O的半径为，设，则，

四棱锥体积最大，当且仅当梯形面积最大，并且点D到平面的距离最大，
显然球面上的点D到平面的最大距离为R，梯形面积，
令，，求导得：，
当时，，当时，，即函数在上递增，在是递减，
因此当时，，，
于是得四棱锥体积的最大值为，解得，
所以球的表面积为.
故选：C
【点睛】思路点睛：涉及某些几何体面积、体积问题最值，可以引入变量建立函数关系，再求解函数最值作答.
3．（2022·浙江·模拟预测）某全球卫星导航系统是我国航天事业的重要成果.在卫星导航系统中，地球静止同步卫星的轨道位于地球赤道所在平面，轨道高度为h（轨道高度是指卫星到地球表面的距离）.将地球看作是一个球心为O，半径r为的球，其上点A的纬度是指OA与赤道平面所成角的度数.地球表面上能直接观测到一颗地球静止同步轨道卫星点的纬度最大值为，记卫星信号覆盖地球表面的表面积为（单位：），若，则S占地球表面积的百分比约为（ ）
A．26%B．34%C．42%D．50%
【答案】C
【分析】设表示卫星，过作截面，截地球得大圆，过作圆的切线，线段交圆于，得，在直角三角形中求出后，可计算两者面积比．
【详解】设表示卫星，过作截面，截地球得大圆，过作圆的切线，线段交圆于，如图，则，，，，
则，又，所以
设地球表面积为，则
所以．
故选：C．
4．（2022·湖南长沙·长沙县第一中学校考模拟预测）已知三棱锥S－ABC中，∠BAC=，SB⊥AB，SC⊥AC，SB=SC=3，，三棱锥体积为，则三棱锥S－ABC外接球的表面积为（ ）
A．5πB．20πC．25πD．100π
【答案】C
【分析】观察△SBA、△SCA均为直角三角形，得到点P为三棱锥S－ABC外接球的球心，且棱锥P－ABC为正三棱锥，可以通过设高|PO|结合求得底面正△ABC的边长a，从而得到外接球半径|PA|，最后求得表面积．
【详解】解：如图，取SA中点P，SB⊥AB，SC⊥AC，则△SBA，△SCA均为直角三角形，
PA=PB=PC=PS，即点P为三棱锥S－ABC外接球球心，PA即为外接球半径，
又SB=SC，故AB=AC且为等边三角形
又PA=PB=PC三棱锥P－ABC为正三棱锥；
作PO⊥平面ABC，垂足为O，连接OA
则O为△ABC的外心，
设正三角形ABC的边长为a，
则，
即，外接球表面积为，故排除A；
∴，故排除D；
若，则，代入方程不成立，故排除B；
若，则，代入方程成立，所以C正确，
故选：C
二、填空题
5．（2022·陕西西安·西安中学校考模拟预测）在三棱锥中，，，，的中点为，的余弦值是，若都在同一球面上，则该球的表面积是 ．
【答案】
【分析】根据二面角的定义可得为的平面角，利用图中的垂直关系和直线与平面垂直的判定定理可得以为顶点可以补成一个棱长为的正方体，则正方体的对角线为球的一条直径，进而可得到三棱锥外接球的表面积,
【详解】如图所示：
因为中点为，连接，，
则由，，得出，，
所以为的平面角，
又因为平面，所以面，
因为面，所以，
又因为，，所以为等腰直角三角形，且，
又因为，故，
在中，，
在中，，
在中，由余弦定理得
，
满足，所以，即，
又，，、面，
所以面，
又因为面，所以两两垂直，
以为顶点可以补成一个棱长为的正方体，
都在正方体的外接球上，则正方体的对角线为球的一条直径，
所以，，
所以球的表面积．
故答案为：．
6．（2022·黑龙江哈尔滨·哈尔滨三中校考模拟预测）在三棱锥中，二面角和的大小都为，，，，则三棱锥的外接球与内切球的表面积的比值为 .
【答案】
【分析】根据等体积法求出内切球半径，设中点为，过作直线的平行线，
三棱锥外接球球心在直线上且位于平面下方，根据求出外接球半径解决即可.
【详解】如图，作平面，垂足为，过作，垂足为，
所以为二面角的平面角，由，大小均为知，点到直线距离相等，即点是的内切圆圆心，设半径为则，
又因为在中，，，，
所以为直角三角形，
，
所以，
设中点为，过作直线的平行线，
所以三棱锥外接球球心在直线上且位于平面下方，
在直角中，过作交于，作交于，
连接，所以与全等，，
因为是中点，
所以，
所以，
所以在直角中，，
设，
所以
又因为，
所以，
解得，
所以，
设内切球半径为，
因为,
所以，
所以，
所以,
故答案为：.
7．（2022·全国·模拟预测）已知圆柱中，AB为底面圆O的直径，，点P为底面圆O上一点，当圆柱的表面积为时，三棱锥的外接球的体积为 ．
【答案】/
【分析】首先根据圆柱的表面积求出圆柱的高，
解法一：设球心到平面ABP的距离为x，最后根据勾股定理得，解得即可求出外接圆半径，进而根据球体体积公式进行求解.
解法二：设三棱锥的外接球的半径为R，延长与球面交于点，连接，
然后得，进而利用直角三角形的射影定理求解出的值，最后根据球体体积公式进行求解.
【详解】因为圆柱的底面直径，表面积为，设圆柱的高为h，得，解得．易知三棱锥的外接球的球心在直线上．
解法一：
如图，设球心到平面ABP的距离为x，外接球半径为，
若球心在三棱锥内部，则，
此时有，解得，不满足题意，故舍去；
若球心在三棱锥外部，则，
此时有，解得，
所以三棱锥的外接球的半径，
所以其外接球的体积．
解法二：
如图，设三棱锥的外接球的半径为R，延长与球面交于点，连接，
则，，易知，则由射影定理得，
即，解得，所以其外接球的体积．
故答案为：
8．（2022·河北沧州·统考二模）三棱锥的平面展开图如图所示，已知，若三棱锥的四个顶点均在球的表面上，则球的表面积为 .
【答案】
【分析】根据题意构造底面正三角形的边长为2，高为的正三棱柱，则该三棱柱的外接球即为三棱锥的外接球，球心即为上下底面外接圆圆心连线的中点，再根据条件求半径即可.
【详解】由已知得，三棱锥中，，
且与平面所成的角为，构造如图所示的正三棱柱，底面正三角形的边长为2，
高为，则该三棱柱的外接球即为三棱锥的外接球.设，分别为三棱柱上､下底面三角形的中心，
则为的中点，因为，
所以球的半径，
所以球的表面积为.
故答案为：.
【点睛】与球有关的组合体问题，一种是内切，一种是外接．解题时要认真分析图形，明确切点和接点的位置，确定有关元素间的数量关系，并作出合适的截面图，如球内切正方体，切点为正方体各个面的中心，正方体的棱长等于球的直径；球外接正方体，正方体的顶点均在球面上，正方体的体对角线长等于球的直径.
三、双空题
9．（2022·广东汕头·统考三模）如图，DE是边长为的正三角形ABC的一条中位线，将△ADE沿DE翻折至，当三棱锥的体积最大时，四棱锥外接球O的表面积为 ；过EC的中点M作球O的截面，则所得截面圆面积的最小值是 ．
【答案】 /
【分析】第一空：先判断出平面平面时，三棱锥的体积最大，求出，找出四棱锥外接球的球心O，由勾股定理求出半径，即可求得表面积；第二空：先判断出当垂直于截面圆时，截面圆面积最小，即为截面圆的直径，再求面积即可.
【详解】
第一空：设到平面的距离为，易得，为定值，
要使三棱锥的体积最大，即最大，显然当平面平面时，最大，取中点，连接交于，
则为中点，连接，易得，又平面平面，则平面，
即最大为，易得，则为四边形的外心，
设的外心为，过作直线平面，易得，则共面，过作直线垂直于平面交直线于，
易得即为外接球球心，连接，即为外接球半径，易得四边形为矩形，则，
，则，故外接球O的表面积为；
第二空：要使截面圆面积最小，显然当垂直于截面圆时，截面圆半径最小，面积最小，又都在球面上，M为EC中点，
显然为截面圆的直径，又，则截面圆的面积最小为.
故答案为：；.
10．（2022·黑龙江哈尔滨·哈九中校考模拟预测）已知正四面体外接球表面积为，则该正四面体棱长为 ；若为平面内一动点，且 ，则最小值为 ．
【答案】 6
【分析】先利用正四面体外接球表面积求出其半径，然后由求出正四面体的棱长，由为平面内一动点，且，则，即点的轨迹为以为圆心，为半径的圆，最后结合点与圆的位置关系求解即可．
【详解】设该正四面体棱长为，
过点作面，
则点为的重心，
则，，
又正四面体外接球表面积为，
则 ，
则，
即，
又，
则，
解得：；
又为平面内一动点，且，
则，
即点的轨迹为以为圆心，为半径的圆，
又，
则由点与圆的位置关系可得最小值为：，
故答案为：；．
【真题感知】
1．（2020·天津·统考高考真题）若棱长为的正方体的顶点都在同一球面上，则该球的表面积为（ ）
A．B．C．D．
【答案】C
【分析】求出正方体的体对角线的一半，即为球的半径，利用球的表面积公式，即可得解.
【详解】这个球是正方体的外接球，其半径等于正方体的体对角线的一半，
即，
所以，这个球的表面积为.
故选：C.
【点睛】本题考查正方体的外接球的表面积的求法，求出外接球的半径是本题的解题关键，属于基础题.求多面体的外接球的面积和体积问题，常用方法有：（1）三条棱两两互相垂直时，可恢复为长方体，利用长方体的体对角线为外接球的直径，求出球的半径；（2）直棱柱的外接球可利用棱柱的上下底面平行，借助球的对称性，球心为上下底面外接圆的圆心连线的中点，再根据勾股定理求球的半径；（3）如果设计几何体有两个面相交，可过两个面的外心分别作两个面的垂线，垂线的交点为几何体的球心.
2．（2020·全国·统考高考真题）已知为球的球面上的三个点，⊙为的外接圆，若⊙的面积为，，则球的表面积为（ ）
A．B．C．D．
【答案】A
【分析】由已知可得等边的外接圆半径，进而求出其边长，得出的值，根据球的截面性质，求出球的半径，即可得出结论.
【详解】设圆半径为，球的半径为，依题意，
得，为等边三角形，
由正弦定理可得，
，根据球的截面性质平面，
，
球的表面积.
故选：A

【点睛】本题考查球的表面积，应用球的截面性质是解题的关键，考查计算求解能力，属于基础题.
3．（2021·全国·统考高考真题）北斗三号全球卫星导航系统是我国航天事业的重要成果．在卫星导航系统中，地球静止同步卫星的轨道位于地球赤道所在平面，轨道高度为（轨道高度是指卫星到地球表面的距离）．将地球看作是一个球心为O，半径r为的球，其上点A的纬度是指与赤道平面所成角的度数．地球表面上能直接观测到一颗地球静止同步轨道卫星点的纬度最大值为，记卫星信号覆盖地球表面的表面积为（单位：），则S占地球表面积的百分比约为（ ）
A．26%B．34%C．42%D．50%
【答案】C
【分析】由题意结合所给的表面积公式和球的表面积公式整理计算即可求得最终结果.
【详解】由题意可得，S占地球表面积的百分比约为：
.
故选：C.
4．（2022·全国·统考高考真题）已知正三棱台的高为1，上、下底面边长分别为和，其顶点都在同一球面上，则该球的表面积为（ ）
A．B．C．D．
【答案】A
【分析】根据题意可求出正三棱台上下底面所在圆面的半径，再根据球心距，圆面半径，以及球的半径之间的关系，即可解出球的半径，从而得出球的表面积．
【详解】设正三棱台上下底面所在圆面的半径，所以，即，设球心到上下底面的距离分别为，球的半径为，所以，，故或，即或，解得符合题意，所以球的表面积为．
故选：A．

5．（2020·全国·统考高考真题）已知△ABC是面积为的等边三角形，且其顶点都在球O的球面上.若球O的表面积为16π，则O到平面ABC的距离为（ ）
A．B．C．1D．
【答案】C
【分析】根据球的表面积和的面积可求得球的半径和外接圆半径，由球的性质可知所求距离.
【详解】
设球的半径为，则，解得：.
设外接圆半径为，边长为，
是面积为的等边三角形，
，解得：，，
球心到平面的距离.
故选：C.
【点睛】本题考查球的相关问题的求解，涉及到球的表面积公式和三角形面积公式的应用；解题关键是明确球的性质，即球心和三角形外接圆圆心的连线必垂直于三角形所在平面.
6．（2021·天津·统考高考真题）两个圆锥的底面是一个球的同一截面，顶点均在球面上，若球的体积为，两个圆锥的高之比为，则这两个圆锥的体积之和为（ ）
A．B．C．D．
【答案】B
【分析】作出图形，计算球体的半径，可计算得出两圆锥的高，利用三角形相似计算出圆锥的底面圆半径，再利用锥体体积公式可求得结果.
【详解】如下图所示，设两个圆锥的底面圆圆心为点，
设圆锥和圆锥的高之比为，即，
设球的半径为，则，可得，所以，，
所以，，，
，则，所以，，
又因为，所以，，
所以，，，
因此，这两个圆锥的体积之和为.
故选：B.
7．（2022·全国·统考高考真题）已知正四棱锥的侧棱长为l，其各顶点都在同一球面上.若该球的体积为，且，则该正四棱锥体积的取值范围是（ ）
A．B．C．D．
【答案】C
【分析】设正四棱锥的高为，由球的截面性质列方程求出正四棱锥的底面边长与高的关系，由此确定正四棱锥体积的取值范围.
【详解】∵球的体积为，所以球的半径,
[方法一]：导数法
设正四棱锥的底面边长为，高为，
则，,
所以，
所以正四棱锥的体积，
所以，
当时，，当时，，
所以当时，正四棱锥的体积取最大值，最大值为，
又时，，时，,
所以正四棱锥的体积的最小值为，
所以该正四棱锥体积的取值范围是.
故选：C.
[方法二]：基本不等式法
由方法一故所以当且仅当取到，
当时，得，则
当时，球心在正四棱锥高线上，此时，
，正四棱锥体积，故该正四棱锥体积的取值范围是
二、填空题
8．（2020·全国·统考高考真题）已知圆锥的底面半径为1，母线长为3，则该圆锥内半径最大的球的体积为 ．
【答案】
【分析】将原问题转化为求解圆锥内切球的问题，然后结合截面确定其半径即可确定体积的值.
【详解】易知半径最大球为圆锥的内切球，球与圆锥内切时的轴截面如图所示，
其中，且点M为BC边上的中点，
设内切圆的圆心为，

由于，故，
设内切圆半径为，则：
，
解得：，其体积：.
故答案为：.
【点睛】与球有关的组合体问题，一种是内切，一种是外接．解题时要认真分析图形，明确切点和接点的位置，确定有关元素间的数量关系，并作出合适的截面图，如球内切于正方体，切点为正方体各个面的中心，正方体的棱长等于球的直径；球外接于正方体，正方体的顶点均在球面上，正方体的体对角线长等于球的直径.