新高考数学一轮复习精品讲练测第7章第04讲 空间中的垂直关系（2份，原卷版+解析版）

这是一份新高考数学一轮复习精品讲练测第7章第04讲 空间中的垂直关系（2份，原卷版+解析版），文件包含新高考数学一轮复习精品讲练测第7章第04讲空间中的垂直关系教师版doc、新高考数学一轮复习精品讲练测第7章第04讲空间中的垂直关系学生版doc等2份试卷配套教学资源，其中试卷共148页， 欢迎下载使用。

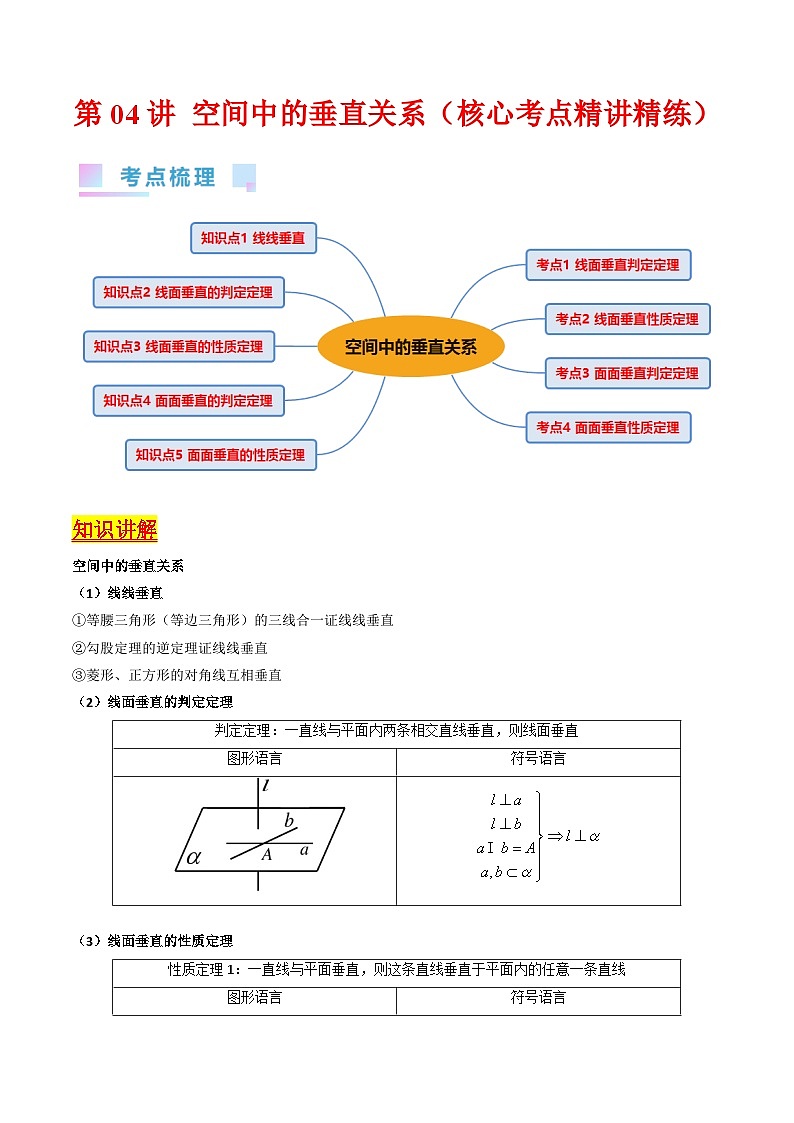
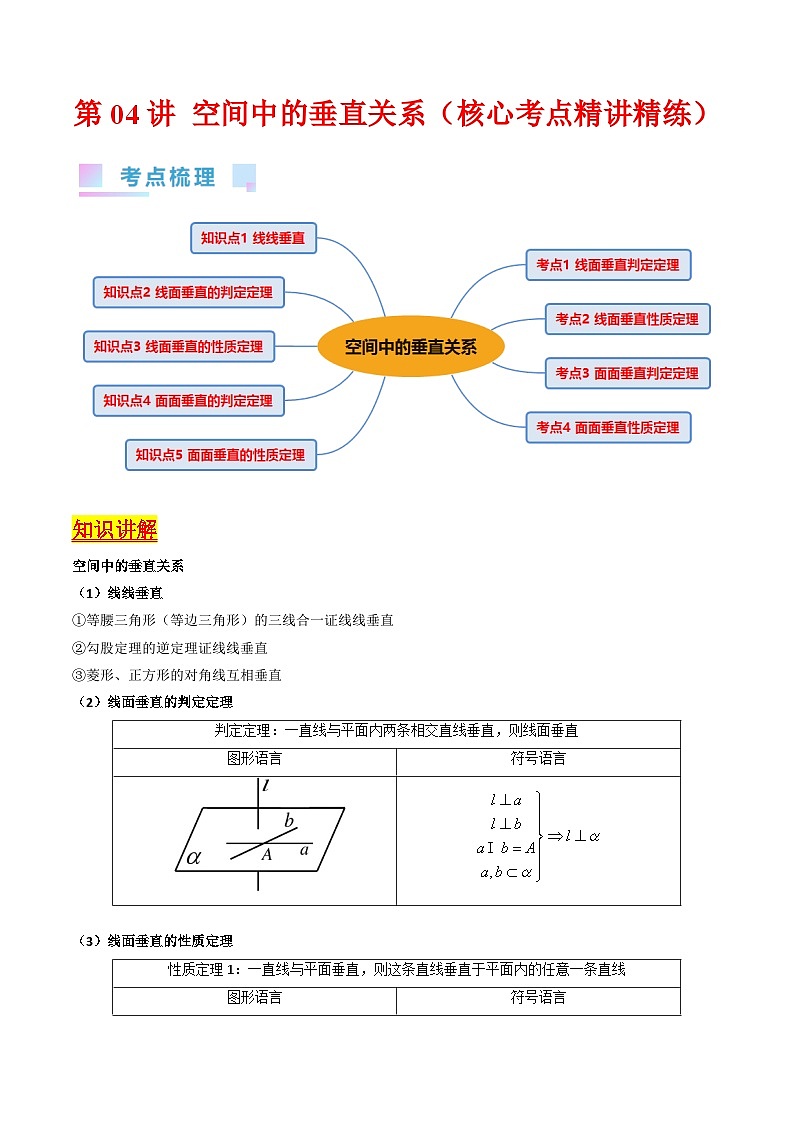
知识讲解
空间中的垂直关系
线线垂直
①等腰三角形（等边三角形）的三线合一证线线垂直
②勾股定理的逆定理证线线垂直
③菱形、正方形的对角线互相垂直
线面垂直的判定定理
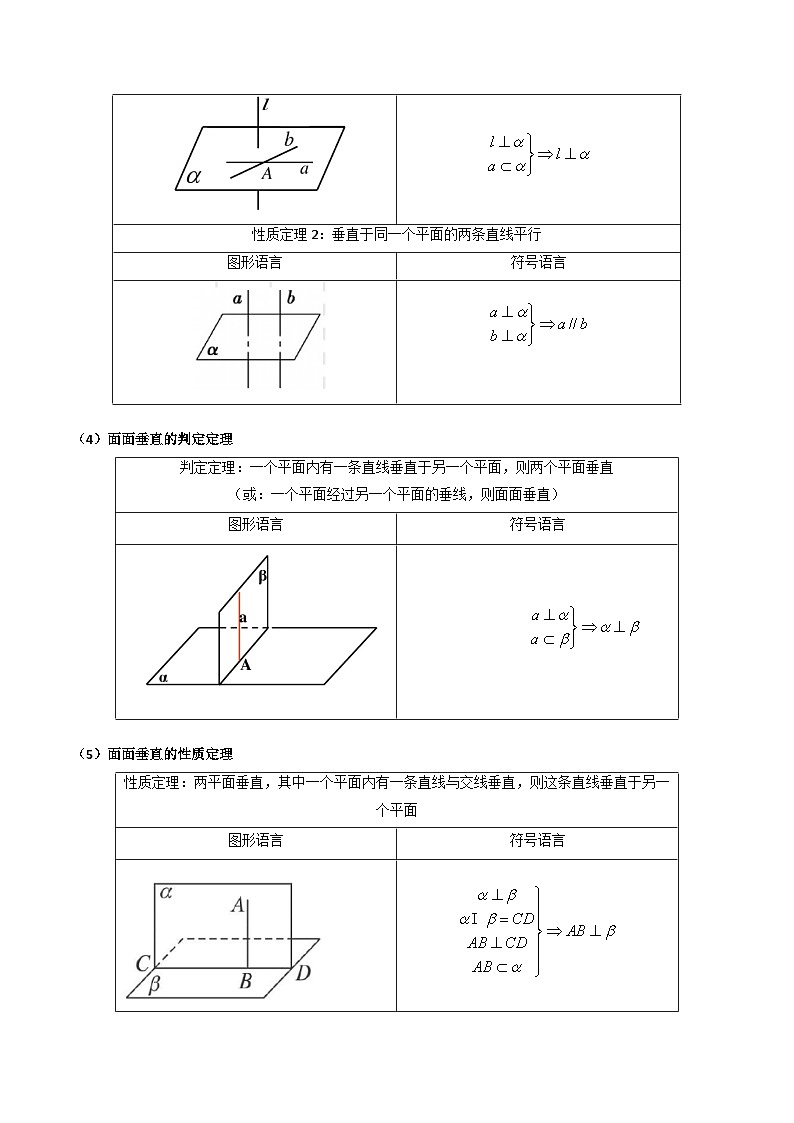
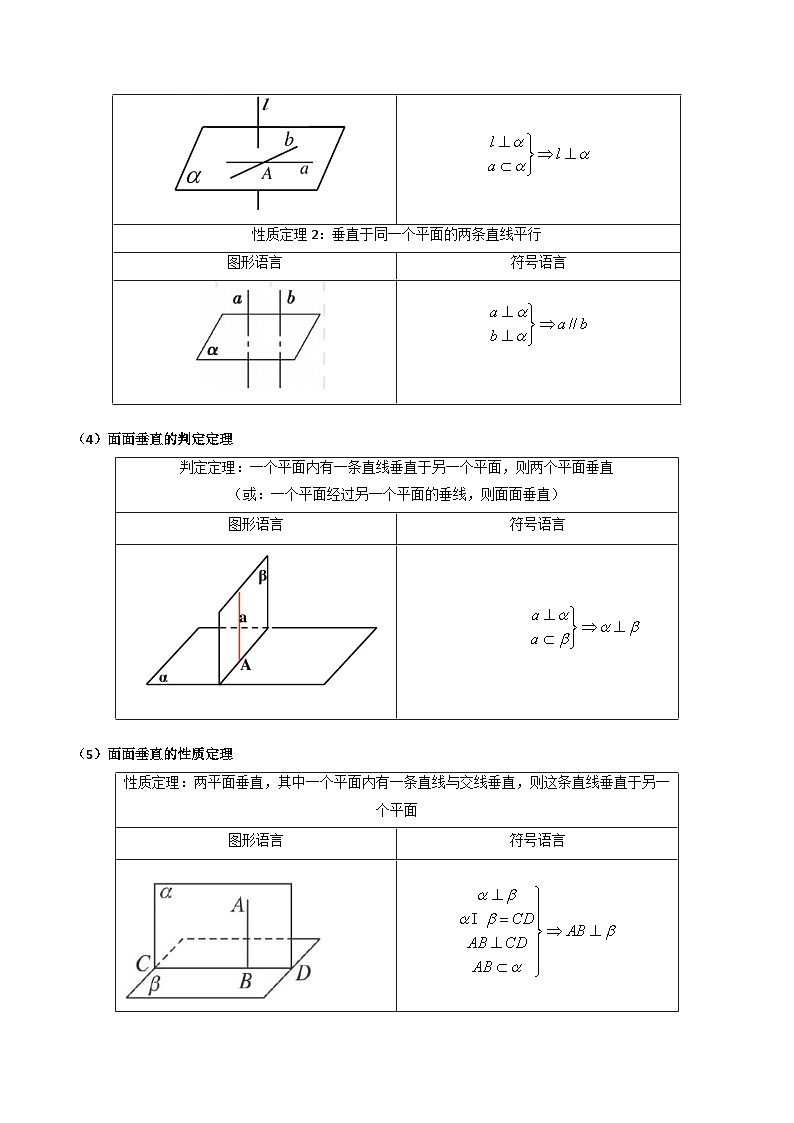
线面垂直的性质定理
面面垂直的判定定理
面面垂直的性质定理
考点一、线面垂直判定定理
1．（2023·四川成都·树德中学校考模拟预测）直三棱柱中，，为的中点，点在上，.

(1)证明：平面；
(2)若二面角大小为，求以为顶点的四面体体积.
2．（2023·江苏徐州·校考模拟预测）在三棱台中，为中点，，，.
(1)求证：平面；
(2)若，，平面与平面所成二面角大小为，求三棱锥的体积.
3．（2023·江苏·金陵中学校联考三模）如图，圆锥中，为底面圆的直径，，为底面圆的内接正三角形，圆锥的高，点为线段上一个动点.

(1)当时，证明：平面；
(2)当点在什么位置时，直线PE和平面所成角的正弦值最大.
4．（2023·湖北黄冈·黄冈中学校考三模）如图1，在四边形中，，．将四边形沿折起，使得，得到如图2所示的几何体．

(1)若为的中点，证明：平面；
(2)若为上一动点，且二面角的余弦值为，求的值．
5．（2023·浙江·校考模拟预测）如图，在四棱锥中，底面为正方形，点在底面内的投影恰为中点，且．
(1)若，求证：面；
(2)若平面与平面所成的锐二面角为，求直线与平面所成角的正弦值．
1．（2023·山东泰安·统考模拟预测）如图，在多面体中，上底面与下底面平行，且都是正方形，该多面体各条侧棱相等，且每条侧棱与底面所成角都相等．已知，垂足为点，三棱锥的体积为．

(1)证明：平面；
(2)求直线与平面所成角的正弦值．
2．（2023·甘肃张掖·高台县第一中学校考模拟预测）如图，在四棱锥P－ABCD中，底面ABCD是平行四边形，PA⊥平面ABCD，，点M在棱PD上，且，．

(1)求证：CD⊥平面PAD；
(2)求BM与平面所成角的余弦值．
3．（2023·内蒙古赤峰·赤峰二中校联考模拟预测）如图1，在五边形中，四边形为正方形，，，如图2，将沿折起，使得A至处，且．

(1)证明：平面；
(2)求二面角的余弦值．
4．（2023·云南·校联考模拟预测）如图，在四棱锥中，已知，.

(1)证明：平面；
(2)若，求平面与平面所成夹角的余弦值.
5．（2023·湖南·校联考模拟预测）在图1中，为等腰直角三角形，，，为等边三角形，O为AC边的中点，E在BC边上，且，沿AC将进行折叠，使点D运动到点F的位置，如图2，连接FO，FB，FE，使得．

(1)证明：平面．
(2)求二面角的余弦值．
考点二、线面垂直性质定理
1．（2023·全国·统考高考真题）如图，三棱锥中，，，，E为BC的中点．

(1)证明：；
(2)点F满足，求二面角的正弦值．
2．（2022·全国·统考高考真题）在四棱锥中，底面．
(1)证明：；
(2)求PD与平面所成的角的正弦值．
3．（2021·全国·高考真题）已知直三棱柱中，侧面为正方形，，E，F分别为和的中点，.
（1）求三棱锥的体积；
（2）已知D为棱上的点，证明：.
4．（2023·河北·校联考模拟预测）在三棱台中，平面，，分别是的中点，是棱上的动点.

(1)求证：；
(2)若是线段的中点，平面与的交点记为，求平面与平面夹角的余弦值.
5．（2023·福建福州·福建省福州第一中学校考模拟预测）已知三棱台，面，，，D是线段中点，且.

(1)证明：；
(2)请选择合适的基底向量，求直线与所成角的余弦值.
1．（2023·江苏南京·统考二模）在梯形中，，，，，如图1．现将沿对角线折成直二面角，如图2，点在线段上．
(1)求证：；
(2)若点到直线的距离为，求的值．
2．（2023·浙江杭州·统考二模）在三棱锥中，底面为等腰直角三角形，.
(1)求证：；
(2)若，求平面与平面夹角的余弦值.
3．（2023·山东日照·三模）如图，在直三棱柱中，，侧面是正方形，且平面平面.

(1)求证：；
(2)若直线与平面所成的角为为线段的中点，求平面与平面所成锐二面角的大小.
4．（2023·湖北武汉·统考模拟预测）已知图1是由等腰直角三角形和菱形组成的一个平面图形，其中菱形边长为4，，．将三角形沿折起，使得平面平面（如图2）．

(1)求证：；
(2)求二面角的正弦值．
5．（2023·广东深圳·统考二模）如图，在四棱锥中，底面为矩形，平面，点是的中点.

(1)证明：；
(2)设的中点为，点在棱上（异于点，，且，求直线与平面所成角的正弦值.
考点三、面面垂直判定定理
1．（2023·全国·统考高考真题）如图，在三棱柱中，平面．

(1)证明：平面平面；
(2)设，求四棱锥的高．
2．（2022·全国·统考高考真题）如图，四面体中，，E为的中点．
(1)证明：平面平面；
(2)设，点F在上，当的面积最小时，求与平面所成的角的正弦值．
3．（2021·全国·统考高考真题）在四棱锥中，底面是正方形，若．
（1）证明：平面平面；
（2）求二面角的平面角的余弦值．
4．（2023·广东梅州·统考三模）如图所示，在几何体中，平面，点在平面的投影在线段上，，，，平面.

(1)证明：平面平面.
(2)若二面角的余弦值为，求线段的长.
5．（2020·全国·统考高考真题）如图，已知三棱柱ABC–A1B1C1的底面是正三角形，侧面BB1C1C是矩形，M，N分别为BC，B1C1的中点，P为AM上一点．过B1C1和P的平面交AB于E，交AC于F．
（1）证明：AA1//MN，且平面A1AMN⊥平面EB1C1F；
（2）设O为△A1B1C1的中心，若AO=AB=6，AO//平面EB1C1F，且∠MPN=，求四棱锥B–EB1C1F的体积．
1．（2023·湖北武汉·武汉二中校联考模拟预测）如图，在三棱柱中，底面是边长为4的等边三角形，在上且满足.

(1)求证：平面平面；
(2)求平面与平面夹角的余弦值.
2．（2023·山东青岛·统考模拟预测）已知平面四边形ABCE（图1）中，，均为等腰直角三角形，M，N分别是AC，BC的中点，，，沿AC将翻折至位置（图2），拼成三棱锥D-ABC.
(1)求证：平面平面；
(2)当二面角的二面角为60°时，
①求直线与平面所成角的正弦值；
②求C点到面ABD的距离.
3．（2023·河北秦皇岛·统考模拟预测）如图，在多面体中，四边形是边长为4的菱形，与交于点平面．

(1)求证：平面平面；
(2)若，点为的中点，求二面角的余弦值．
4．（2023·辽宁沈阳·统考一模）如图，在矩形ABCD中，，E为边CD上的点，，以BE为折痕把折起，使点C到达点P的位置，且使二面角为直二面角，三棱锥的体积为．
(1)求证：平面平面PAE；
(2)求二面角的余弦值．
5．（2023·江苏镇江·扬中市第二高级中学校考模拟预测）如图，在以P，A，B，C，D为顶点的五面体中，四边形ABCD为等腰梯形，，，平面平面，．
(1)求证：平面平面；
(2)若二面角的余弦值为，求直线PD与平面PBC所成角的大小．
考点四、面面垂直性质定理
1．（2021·全国·统考高考真题）如图，在三棱锥中，平面平面，，为的中点.
（1）证明：；
（2）若是边长为1的等边三角形，点在棱上，，且二面角的大小为，求三棱锥的体积.
2．（2023·辽宁葫芦岛·统考二模）在三棱柱中，平面平面，侧面为菱形，，，，E是AC的中点.

(1)求证：平面
(2)确定在线段上是否存在一点P，使得AP与平面所成角为，若存在，求出的值;若不存，说明理由.
3．（2023·山东泰安·统考二模）如图，在三棱锥中，平面平面，为等边三角形，D，E分别为，的中点，，，.
(1)求证：平面；
(2)在线段上是否存在点F，使得平面与平面的夹角为，若存在，求出的长；若不存在，请说明理由．
4．（2023·四川成都·校联考二模）如图，平面平面，四边形为矩形，为正三角形，，为的中点.

(1)证明：平面平面；
(2)已知四棱锥的体积为，求点到平面的距离.
1．（2023·河北唐山·统考三模）如图所示，在三棱锥中，已知平面，平面平面，点为线段上一点，且.
(1)证明：平面；
(2)若，，且三棱锥的体积为18，求平面与平面的夹角的余弦值.
2．（2023·江苏·统考一模）在三棱柱中，平面平面，侧面为菱形，，，，是的中点.

(1)求证：平面；
(2)点在线段上（异于点，），与平面所成角为，求的值.
3．（2023·浙江·统考二模）如图，在三棱柱中，底面平面，是正三角形，是棱上一点，且，.
(1)求证：；
(2)若且二面角的余弦值为，求点到侧面的距离.
4．（2023·全国·校联考模拟预测）已知三棱锥ABCD，D在面ABC上的投影为O，O恰好为△ABC的外心．，.
(1)证明：BC⊥AD；
(2)E为AD上靠近A的四等分点，若三棱锥A-BCD的体积为，求二面角的余弦值．
【基础过关】
1．（2023·湖南长沙·雅礼中学校考模拟预测）如图，在三棱锥中，已知，是的中点.
(1)求证：平面平面；
(2)若，求平面与平面夹角的正弦值.
2．（2023·山东·沂水县第一中学校联考模拟预测）如图，在梯形ABCD中，，，，E为边AD上的点，，，将沿直线CE翻折到的位置，且，连接PA，PB．
(1)证明：；
(2)Q为线段PA上一点，且，若二面角的大小为，求实数λ的值．
3．（2023·云南大理·统考模拟预测）如图，在正三棱柱中，底面边长为2，，D为的中点，点E在棱上，且，点P为线段上的动点．
(1)求证：；
(2)若直线与所成角的余弦值为，求平面和平面的夹角的余弦值．
4．（2023·安徽滁州·校考模拟预测）如图，四棱锥的底面是边长为2的菱形，为的中点，.
(1)证明：平面平面.
(2)若，且二面角的大小为，求四棱锥的体积.
5．（2023·辽宁锦州·统考模拟预测）在直角梯形中（如图一），，，.将沿折起，使（如图二）.

(1)求证：平面平面；
(2)设为线段的中点，求点到直线的距离.
6．（2023·广东广州·广州市从化区从化中学校考模拟预测）如图，C是以为直径的圆O上异于A，B的点，平面平面，为正三角形，E，F分别是棱上的点，且满足．
(1)求证：；
(2)是否存在，使得直线与平面所成角的正弦值为？若存在，求出的值；若不存在，请说明理由．
7．（2023·湖北武汉·统考三模）如图，四棱锥中，底面是平行四边形，侧面是等边三角形，平面平面，，．
(1)证明：；
(2)点Q在侧棱上，，过B，Q两点作平面，设平面与，分别交于点E，F，当直线时，求二面角的余弦值．
8．（2023·江苏泰州·统考一模）如图，在中，是边上的高，以为折痕，将折至的位置，使得.
(1)证明：平面；
(2)若，求二面角的正弦值.
9．（2023·山东·沂水县第一中学校联考模拟预测）已知多面体中，四边形是边长为4的正方形，四边形是直角梯形，，，．
(1)求证：平面平面；
(2)求直线与平面所成角的正弦值．
10．（2023·广东惠州·统考模拟预测）如图，在四棱锥P-ABCD中，底面ABCD为正方形，底面ABCD，，E为线段PB的中点，F为线段BC上的动点．
(1)证明：平面平面PBC；
(2)若直线AF与平面PAB所成的角的余弦值为，求点P到平面AEF的距离．
【能力提升】
1．（2023·云南昆明·昆明一中校考模拟预测）在三棱锥中，，，M为棱BC的中点.
(1)证明：；
(2)若平面平面ABC，，，E为线段PC上一点，，求点E到平面PAM的距离.
2．（2023·重庆万州·重庆市万州第二高级中学校考三模）如图，在三棱柱中，平面 .
(1)求证:;
(2)若，直线与平面所成的角为 ，求二面角的正弦值.
3．（2023·广东东莞·东莞实验中学校考一模）如图，为圆柱的轴截面，是圆柱上异于，的母线.
(1)证明：平面DEF；
(2)若，当三棱锥的体积最大时，求二面角的余弦值.
4．（2023·广东佛山·华南师大附中南海实验高中校考模拟预测）如图，在几何体ABCDE中，面，，，．
(1)求证：平面平面DAE；
(2)AB=1，，，求CE与平面DAE所成角的正弦值．
5．（2023·湖南张家界·统考二模）如图，已知三棱柱，，，为线段上的动点，.
(1)求证：平面平面；
(2)若，D为线段的中点，，求与平面所成角的余弦值.
6．（2023·湖北·校联考模拟预测）如图所示，在梯形中，，，四边形为矩形，且平面，.
（1）求证：平面；
（2）点在线段上运动，设平面与平面所成锐二面角为，试求的取值范围.
7．（2023·福建厦门·厦门一中校考模拟预测）如图，圆台下底面圆的直径为， 是圆上异于的点，且，为上底面圆的一条直径，是边长为的等边三角形，.
(1)证明：平面；
(2)求平面和平面夹角的余弦值.
8．（2023·云南·统考模拟预测）如图，四棱锥中，底面ABCD是直角梯形，，，.
(1)求证：平面ABCD；
(2)设，当平面PAM与平面PBD夹角的余弦值为时，求的值.
9．（2023·江苏苏州·苏州市第五中学校校考模拟预测）已知直三棱柱，为线段的中点，为线段的中点，，平面平面.
(1)证明：；
(2)三棱锥的外接球的表面积为，求平面与平面夹角的余弦值.
10．（2023·辽宁本溪·本溪高中校考模拟预测）如图，在四棱锥中，平面平面，，，，，.为的中点，点在上，且.

(1)求证：平面；
(2)在棱上是否存在点，使得点到平面的距离为，若存在求出点的位置，不存在请说明理由.
【真题感知】
1．（2020·全国·统考高考真题）如图，为圆锥的顶点，是圆锥底面的圆心，是底面的内接正三角形，为上一点，∠APC=90°．
（1）证明：平面PAB⊥平面PAC；
（2）设DO=，圆锥的侧面积为，求三棱锥P−ABC的体积.
2．（2020·江苏·统考高考真题）在三棱柱ABC-A1B1C1中，AB⊥AC，B1C⊥平面ABC，E，F分别是AC，B1C的中点．
（1）求证：EF∥平面AB1C1；
（2）求证：平面AB1C⊥平面ABB1．
3．（2020·海南·高考真题）如图，四棱锥P-ABCD的底面为正方形，PD底面ABCD．设平面PAD与平面PBC的交线为．
（1）证明：平面PDC；
（2）已知PD=AD=1，Q为上的点，QB=，求PB与平面QCD所成角的正弦值．
4．（2022·浙江·统考高考真题）如图，已知和都是直角梯形，，，，，，，二面角的平面角为．设M，N分别为的中点．
(1)证明：；
(2)求直线与平面所成角的正弦值．
5．（2023·全国·统考高考真题）如图，在三棱柱中，底面ABC，，到平面的距离为1．

(1)证明：；
(2)已知与的距离为2，求与平面所成角的正弦值．
6．（山东·高考真题）在如图所示的几何体中,四边形是正方形,平面分别为的中点,且
(1)求证:平面平面;
(2)求三棱锥与四棱锥的体积之比.
7．（2023·北京·统考高考真题）如图，在三棱锥中，平面，．

(1)求证：平面PAB；
(2)求二面角的大小．
8．（福建·高考真题）如图，正三棱柱的所有棱长都为
， 为 中点．
（Ⅰ）求证：平面 ；
（Ⅱ）求二面角的大小；
（Ⅲ）求点到平面 的距离．
9．（全国·高考真题）如图，三棱柱中，点在平面ABC内的射影D在AC上，，.
（1）证明：；
（2）设直线与平面的距离为，求二面角的大小.
10．（浙江·高考真题）如图，在三棱柱-中， ，， ，在底面 的射影为的中点， 为的中点.
（1）证明：D 平面；
（2）求二面角-BD- 的平面角的余弦值.
判定定理：一直线与平面内两条相交直线垂直，则线面垂直
图形语言
符号语言
性质定理1：一直线与平面垂直，则这条直线垂直于平面内的任意一条直线
图形语言
符号语言
性质定理2：垂直于同一个平面的两条直线平行
图形语言
符号语言
判定定理：一个平面内有一条直线垂直于另一个平面，则两个平面垂直
（或：一个平面经过另一个平面的垂线，则面面垂直）
图形语言
符号语言
性质定理：两平面垂直，其中一个平面内有一条直线与交线垂直，则这条直线垂直于另一个平面
图形语言
符号语言