新高考数学一轮复习精品讲练测第8章第01讲 直线方程及直线间的位置关系（2份，原卷版+解析版）

这是一份新高考数学一轮复习精品讲练测第8章第01讲 直线方程及直线间的位置关系（2份，原卷版+解析版），文件包含新高考数学一轮复习精品讲练测第8章第01讲直线方程及直线间的位置关系教师版doc、新高考数学一轮复习精品讲练测第8章第01讲直线方程及直线间的位置关系学生版doc等2份试卷配套教学资源，其中试卷共57页， 欢迎下载使用。

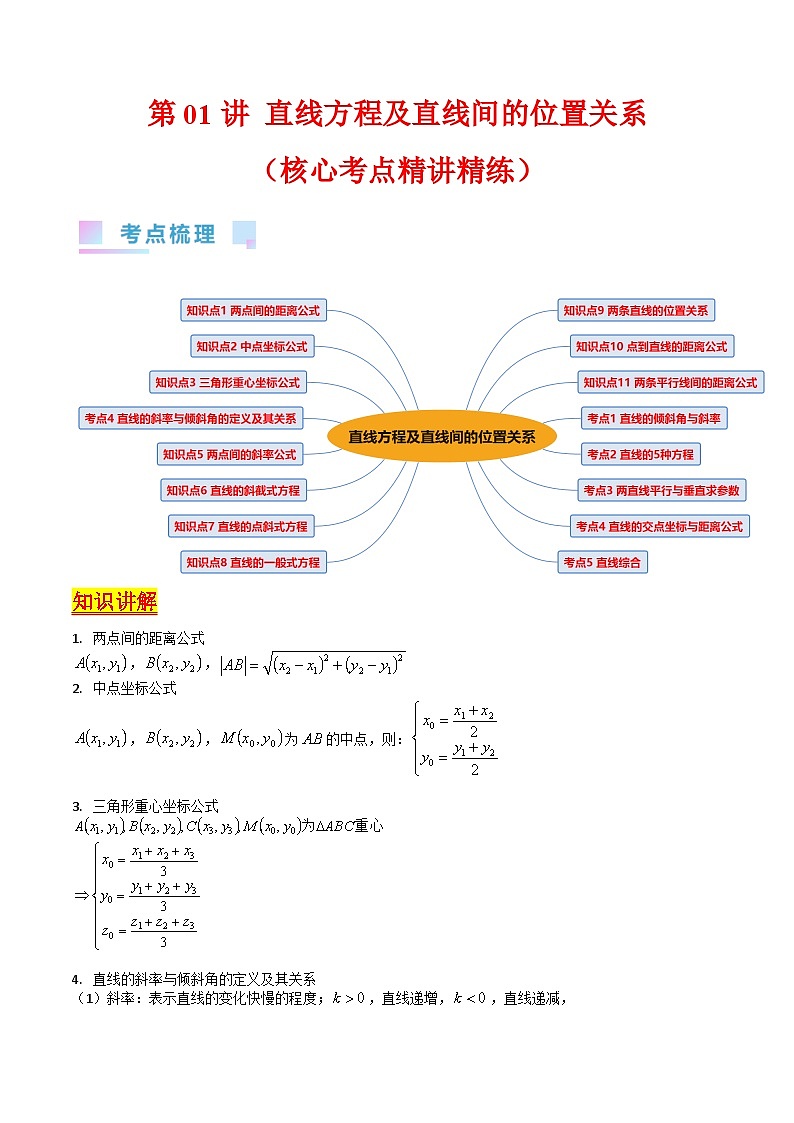
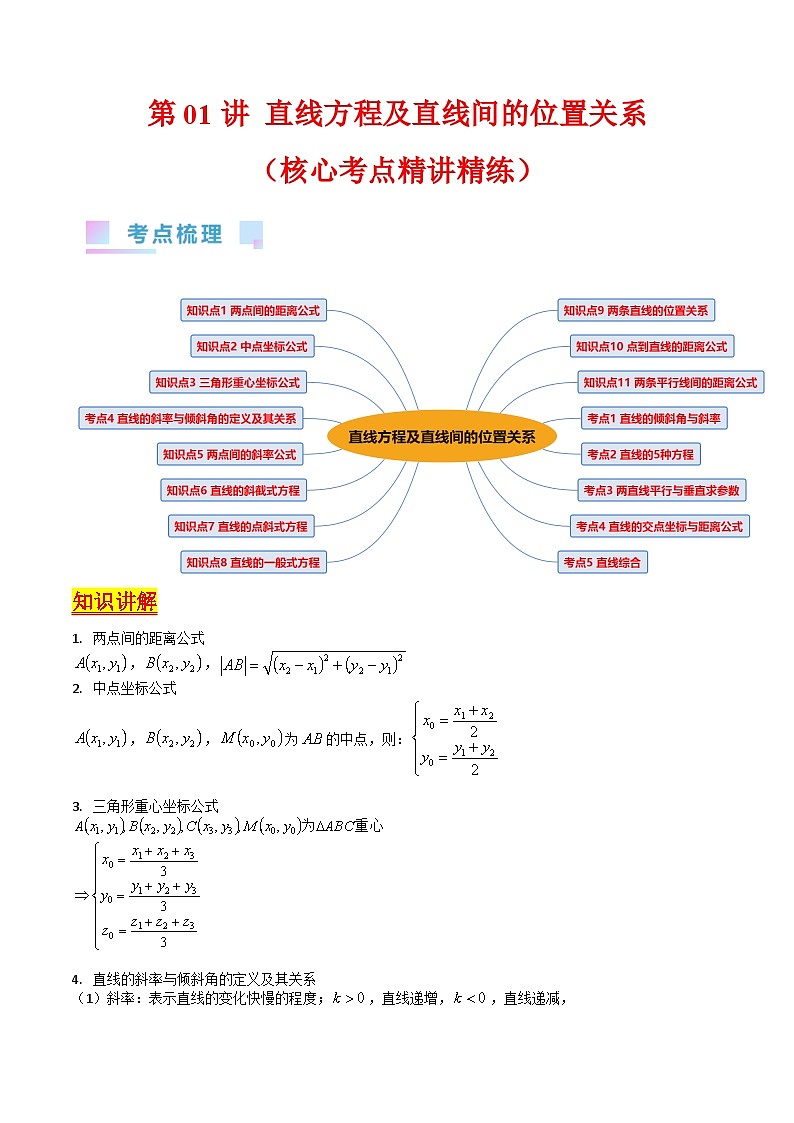
知识讲解
两点间的距离公式
，，
中点坐标公式
，，为的中点，则：
三角形重心坐标公式
直线的斜率与倾斜角的定义及其关系
斜率：表示直线的变化快慢的程度；，直线递增，，直线递减，
倾斜角：直线向上的部分与轴正方向的夹角，范围为
直线的斜率与倾斜角的关系：
两点间的斜率公式
，，
直线的斜截式方程
，其中为斜率，为轴上的截距
直线的点斜式方程
已知点，直线的斜率，则直线方程为：
直线的一般式方程
两条直线的位置关系
平行的条件
①斜截式方程：，，
②一般式方程：，，
重合的条件
①斜截式方程：，，
②一般式方程：
，，
垂直的条件
①斜截式方程：，，
②一般式方程：
，，
点到直线的距离公式
点，直线，点到直线的距离为：
两条平行线间的距离公式
，，
考点一、直线的倾斜角与斜率
1．（2023·全国·高三专题练习）直线的倾斜角为（ ）
A．30°B．45°C．120°D．150°
2．（2023·全国·高三专题练习）如图，若直线的斜率分别为，则（ ）

A．B．
C．D．
3．（2023·全国·高三专题练习）设，为实数，已知直线的斜率，且，，是这条直线上的三个点，则（ ）
A．4B．3C．D．1
4．（2023·全国·高三专题练习）已知直线的方程为，，则直线的倾斜角范围是（ ）
A．B．
C．D．
1．（2023·全国·高三专题练习）直线的倾斜角为（ ）
A．B．C．D．
2．（2023·全国·高三专题练习）已知直线的倾斜角为，则实数的值为（ ）
A．B．C．D．
3．（2023·全国·高三专题练习）函数的图像上有一动点，则在此动点处切线的倾斜角的取值范围为（ ）
A．B．
C．D．
4．（2023·全国·高三专题练习）如图，在平面直角坐标系中，以为始边，角与的终边分别与单位圆相交于，两点，且，，若直线的斜率为，则（ ）

A．B．C．D．
考点二、直线的5种方程
1．（2020·山东·统考高考真题）已知直线的图像如图所示，则角是（ ）
A．第一象限角B．第二象限角C．第三象限角D．第四象限角
2．（2023·福建龙岩·福建省龙岩第一中学校考模拟预测）中，，，，则边上的高所在的直线方程是（ ）
A．B．
C．D．
3．（2023·全国·高三专题练习）已知直线过点，，则直线的方程为（ ）
A．B．C．D．
4．（2023·全国·高三专题练习）如果，，那么直线不通过（ ）．
A．第一象限B．第二象限
C．第三象限D．第四象限
5．（2023·全国·高三专题练习）直线恒过定点（ ）
A．B．C．D．
6．（2023·全国·高三专题练习）过点且在轴、轴上截距相等的直线方程为 .
7．（2023·全国·高三专题练习）倾斜角为135°，在y轴上的截距为﹣1的直线方程是（ ）
A．x﹣y+1＝0B．x﹣y﹣1＝0C．x+y﹣1＝0D．x+y+1＝0
1．（2023·全国·高三专题练习）直线l：的斜率和在x轴上的截距分别为（ ）
A．，3B．，C．，3D．，
2．（2023·江西吉安·江西省泰和中学校考一模）已知的三个顶点为，则边上的高所在直线的方程为 .
3．（2023·新疆喀什·校考模拟预测）已知，则线段AB的垂直平分线的一般方程为 .
4．（2023·全国·高三专题练习）求过点，并且在两轴上的截距相等的直线方程 ．
5．（2023·全国·高三专题练习）直线恒过定点（ ）
A．B．C．D．
6．（2023·全国·高三专题练习）已知直线 则当变化时，直线都通过定点
7．（2023·全国·高三专题练习）已知菱形ABCD的三个顶点､､.
(1)求顶点D的坐标；
(2)求对角线AC和BD所在直线的方程.
考点三、两直线平行与垂直求参数
1．（2023·辽宁丹东·统考二模）直线与直线平行，则（ ）
A．-2B．1C．-2或1D．-1或2
2．（2023·陕西安康·统考二模）已知直线：，：，则“”是“”的（ ）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
3．（2023·黑龙江哈尔滨·哈尔滨市第四中学校校考模拟预测）若曲线在原点处的切线与直线垂直，则实数a的值是（ ）
A．3B．C．1D．0
4．（2023·山东·山东省实验中学校联考模拟预测）若曲线在点处的切线与直线垂直，则的值为（ ）
A．B．C．D．1
5．（2023·吉林·统考二模）已知，若直线与直线垂直，则的最小值为（ ）
A．1B．3C．8D．9
6．（2023·全国·高三专题练习）已知直线，，且，则的最小值为（ ）
A．B．C．D．
1．（2023·江西·江西师大附中校考三模）若为实数，则“”是“直线与平行”的（ ）条件
A．充分不必要B．必要不充分
C．充要D．既不充分也不必要
2．（2023·江苏无锡·江苏省天一中学校考模拟预测）直线与平行，则实数（ ）
A．B．C．或D．0
3．（2023·全国·高三专题练习）直线过点且与直线垂直，则的方程是（ ）
A．B．
C．D．
4．（2023·河南开封·校考模拟预测）已知函数的图象在点处的切线与直线互相垂直，则实数 ．
5．（2023·黑龙江大庆·统考二模）直线l经过点，，若直线l与直线平行，则 ．
6．（2023·江苏扬州·江苏省高邮中学校考模拟预测）（多选）已知直线l1：，l2：，l3：，l4：.则（ ）
A．存在实数α，使l1l2，
B．存在实数α，使l2l3；
C．对任意实数α，都有l1⊥l4
D．存在点到四条直线距离相等
考点四、直线的交点坐标与距离公式
1．（2023·全国·高三专题练习）已知、，则（ ）．
A．B．C．D．
2．（2020·山东·统考高考真题）直线关于点对称的直线方程是（ ）
A．B．
C．D．
3．（2020·全国·统考高考真题）点(0，﹣1)到直线距离的最大值为（ ）
A．1B．C．D．2
4．（2023·全国·高三专题练习）设为动点到直线的距离，则的最大值为（ ）
A．B．C．D．3
5．（2023·全国·高三专题练习）已知两条直线，，则这两条直线之间的距离为（ ）
A．2B．3C．5D．10
6．（2023·全国·高三专题练习）若平面内两条平行线：，：间的距离为，则实数（ ）
A．2B．－2或1C．－1D．－1或2
1．（2023·全国·高三专题练习）在平面直角坐标系中，已知点，，则（ ）
A．1B．C．D．2
2．（2023·全国·高三专题练习）经过两条直线和的交点，并且垂直于直线的直线的方程为（ ）
A．B．
C．D．
3．（2023·全国·高三专题练习）已知直线与互相平行，则它们之间的距离是（ ）
A．4B．C．D．
4．（2023·全国·高三专题练习）直线关于直线对称的直线方程是（ ）
A．B．
C．D．
5．（2023·全国·高三专题练习）设直线与关于直线对称，则直线的方程是（ ）
A．B．
C．D．
6．（2023·全国·高三专题练习）已知两条直线，，且，当两平行线距离最大时，（ ）
A．3B．4C．5D．6
考点五、直线综合
1．（2023·全国·高三专题练习）在平面直角坐标系xOy(O为坐标原点)中，不过原点的两直线，的交点为P，过点O分别向直线，引垂线，垂足分别为M，N，则四边形OMPN面积的最大值为（ ）
A．3B．C．5D．
2．（2023·全国·高三专题练习）已知点A在直线上，点B在直线上，线段AB的中点为，且满足，则的取值范围为（ ）
A．B．C．D．
3．（2023·全国·高三专题练习）已知，则的最小值为（ ）
A．B．C．D．
4．（2023·全国·高三专题练习）的顶点，边上的中线所在的直线为，的平分线所在直线方程为，求边所在直线的方程（ ）
A．B．
C．D．
5．（2023·全国·高三专题练习）已知点，直线，则点到直线的距离的取值范围为 .
6．（2023·全国·高三专题练习）已知､分别在直线与直线上，且，点，，则的最小值为 .
1．（2023·全国·高三专题练习）过点P(3，0)有一条直线l，它夹在两条直线l1：2x－y－2＝0与l2：x＋y＋3＝0之间的线段恰被点P平分，则直线l的方程为 ．
2．（2023·全国·高三专题练习）已知直线，若直线l在两坐标轴上的截距相等，则实数k的值为 ；若直线l不经过第三象限，则k的取值范围是 .
3．（2023秋·山西大同·高三大同市第三中学校校考阶段练习）设点和，在直线：上找一点，使取到最小值，则这个最小值为
4．（2023·全国·高三专题练习）过定点作两条相互垂直的直线、，设原点到直线、的距离分别为、，则的最大值是 ．
5．（2023·全国·高三专题练习）已知的顶点，、边中线方程分别为、，则直线的方程为 ．
6．（2023·全国·高三专题练习）在平面直角坐标系中，若动点到两直线和的距离之和为，则的最大值为 .
【基础过关】
一、单选题
1．（2023·海南海口·海南华侨中学校考二模）若直线与直线的交点在直线上，则实数（ ）
A．4B．2C．D．
2．（2023·广东深圳·统考二模）若过点的直线与圆交于两点，则弦最短时直线的方程为（ ）
A．B．
C．D．
3．（2023·云南·云南师大附中校考模拟预测）已知圆：，直线：被圆截得的弦长为（ ）
A．B．C．D．
4．（2023·河南·校联考模拟预测）圆上的点到直线距离的取值范围是（ ）.
A．B．C．D．
二、填空题
5．（2023·北京丰台·统考二模）已知点，直线，则过点P且与直线l相交的一条直线的方程是 ．
6．（2023·上海徐汇·南洋中学校考三模）已知直线，，若，则 .
7．（2023·河北秦皇岛·统考模拟预测）已知圆，直线与圆C相交于M，N两点，则 ．
8．（2023·四川绵阳·绵阳南山中学实验学校校考模拟预测）已知直线过定点A，直线过定点，与相交于点，则 ．
9．（2023·黑龙江大庆·统考二模）直线l经过点，，若直线l与直线平行，则 ．
10．（2023·重庆·统考二模）已知直线经过点，且，两点到直线的距离相等，则的方程为 .
【能力提升】
一、单选题
1．（2023·山东泰安·统考模拟预测）已知直线与圆，过直线上的任意一点向圆引切线，设切点为，若线段长度的最小值为，则实数的值是（ ）
A．B．C．D．
2．（2023·辽宁锦州·统考模拟预测）已知直线的倾斜角为，则（ ）
A．-3B．C．D．
3．（2023·江西·校联考模拟预测）已知直线，，的斜率分别为，，倾斜角分别为，，，则（ ）
A．B．
C．D．
4．（2023·甘肃陇南·统考一模）斜拉桥是将梁用若干根斜拉索拉在塔柱上的桥，它由梁、斜拉索和塔柱三部分组成.如图1，这是一座斜拉索大桥，共有10对永久拉索，在索塔两侧对称排列.如图2，已知拉索上端相邻两个锚的间距约为4m，拉索下端相邻两个锚的间距均为18m.最短拉索的锚，满足，，以所在直线为轴，所在直线为轴，则最长拉索所在直线的斜率为（ ）

A．B．C．D．
5．（2023·云南·校联考模拟预测）若，则的最小值为（ ）
A．B．C．D．
6．（2023·四川绵阳·四川省绵阳南山中学校考模拟预测）若曲线上恰有三个不同的点到直线的距离为，则实数a的值为（ ）
A．-3B．C．1D．-3或1
二、多选题
7．（2023·广西南宁·南宁二中校联考模拟预测）已知直线，是圆上的一点，则（ ）
A．直线过定点B．圆C的半径是
C．点P可能在圆上D．点P到直线的最大距离是
三、填空题
8．（2023·福建厦门·厦门一中校考模拟预测）已知直线：关于直线的对称直线为轴，则的方程为 .
9．（2023·安徽·池州市第一中学校联考模拟预测）已知函数（其中）在处的切线为，则直线过定点的坐标为 .
10．（2023·河南·校联考模拟预测）已知点，点是直线上任意一点，且，则实数的取值范围是 ．
【真题感知】
一、单选题
1．（2021·全国·高考真题）点到双曲线的一条渐近线的距离为（ ）
A．B．C．D．
2．（2021·全国·统考高考真题）抛物线的焦点到直线的距离为，则（ ）
A．1B．2C．D．4
3．（2022·全国·统考高考真题）图1是中国古代建筑中的举架结构，是桁，相邻桁的水平距离称为步，垂直距离称为举，图2是某古代建筑屋顶截面的示意图．其中是举，是相等的步，相邻桁的举步之比分别为．已知成公差为0.1的等差数列，且直线的斜率为0.725，则（ ）
A．0.75B．0.8C．0.85D．0.9
二、填空题
4．（江苏·高考真题）在平面直角坐标系中，P是曲线上的一个动点，则点P到直线x+y=0的距离的最小值是 .
5．（2021·全国·统考高考真题）双曲线的右焦点到直线的距离为 ．
6．（2021·全国·统考高考真题）已知函数，函数的图象在点和点的两条切线互相垂直，且分别交y轴于M，N两点，则取值范围是 ．
三、双空题
7．（北京·统考高考真题）已知双曲线，则C的右焦点的坐标为 ；C的焦点到其渐近线的距离是 ．
不存在