新高考数学一轮复习精品讲练测第8章第06讲 抛物线方程及其性质（2份，原卷版+解析版）

这是一份新高考数学一轮复习精品讲练测第8章第06讲 抛物线方程及其性质（2份，原卷版+解析版），文件包含新高考数学一轮复习精品讲练测第8章第06讲抛物线方程及其性质教师版doc、新高考数学一轮复习精品讲练测第8章第06讲抛物线方程及其性质学生版doc等2份试卷配套教学资源，其中试卷共96页， 欢迎下载使用。

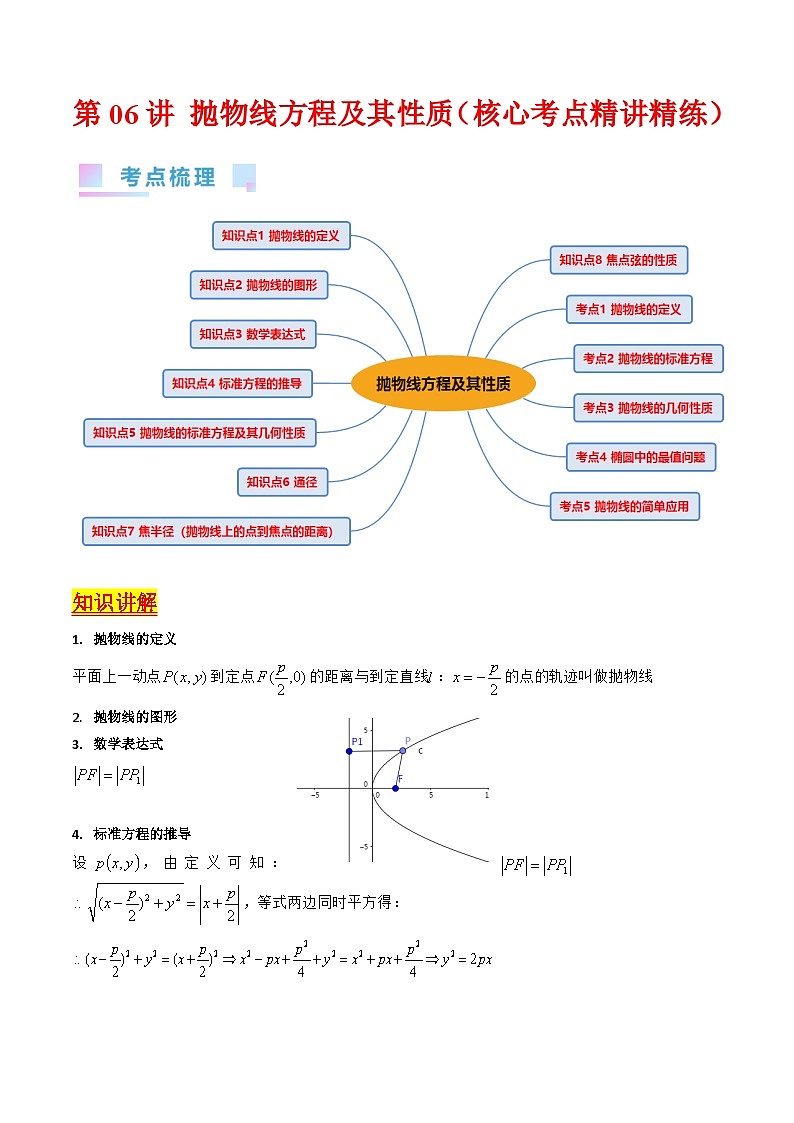
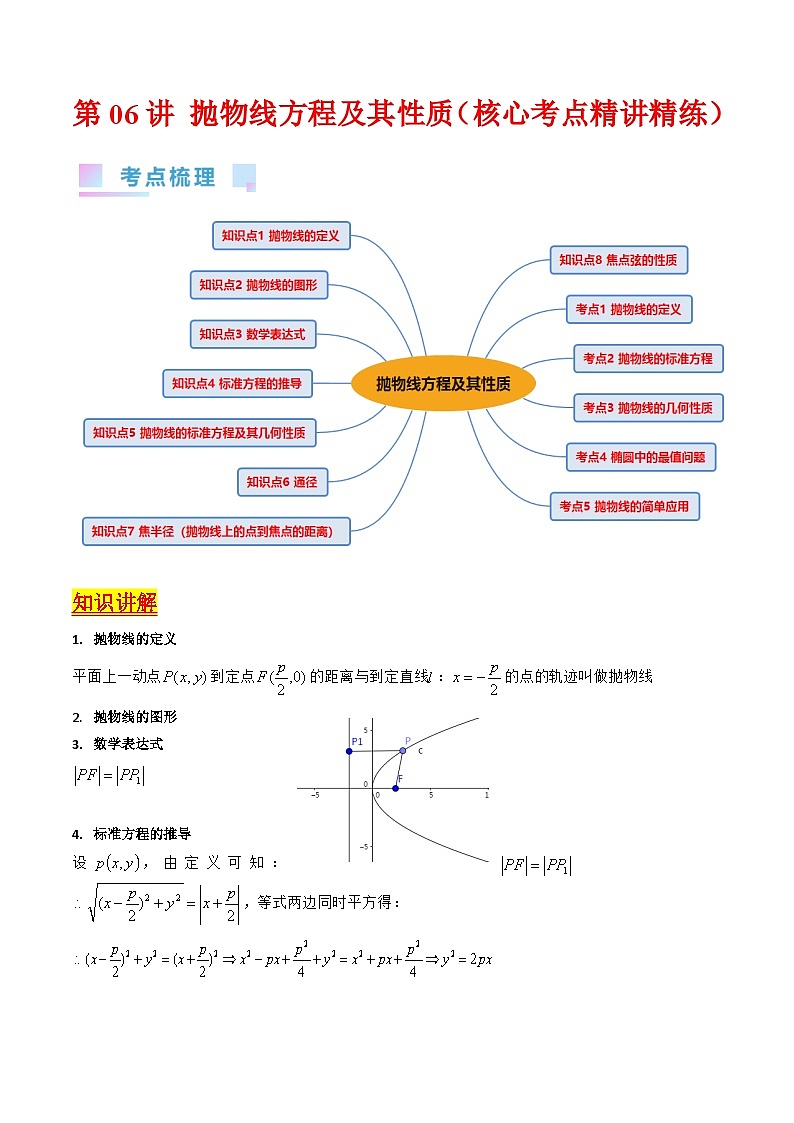
知识讲解
抛物线的定义
平面上一动点到定点的距离与到定直线：的点的轨迹叫做抛物线
抛物线的图形
数学表达式
标准方程的推导
设，由定义可知：，等式两边同时平方得：
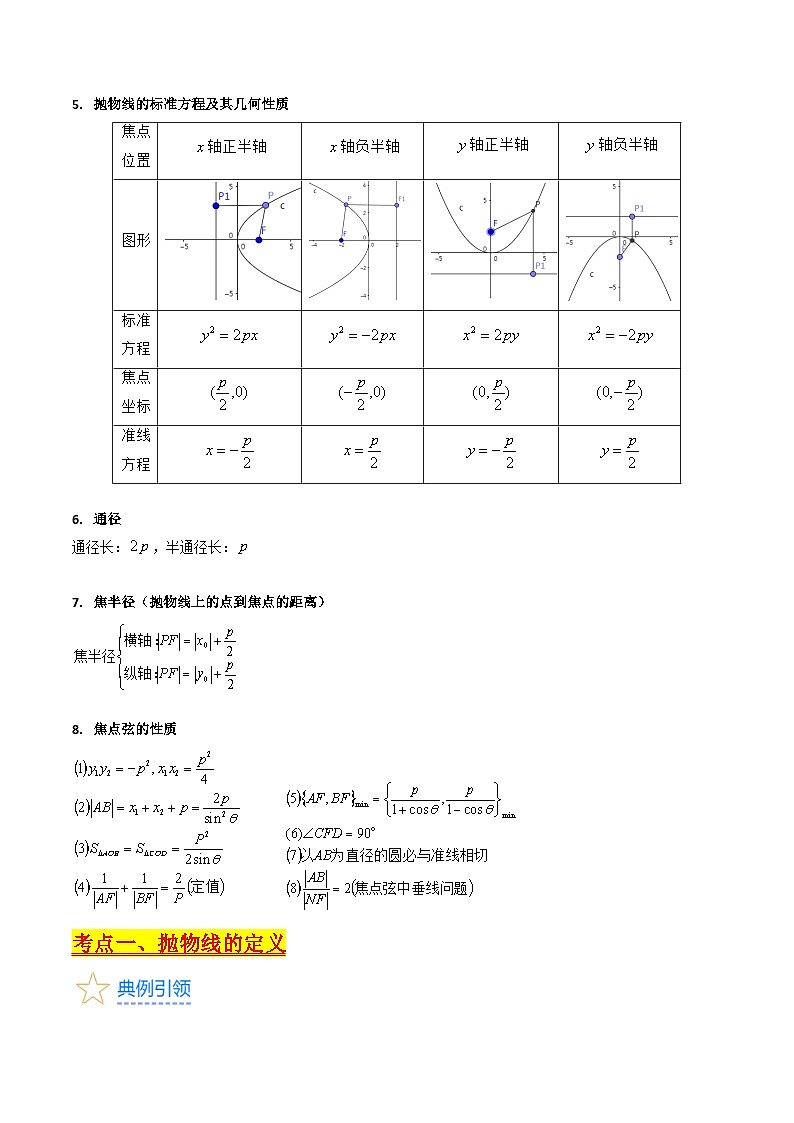
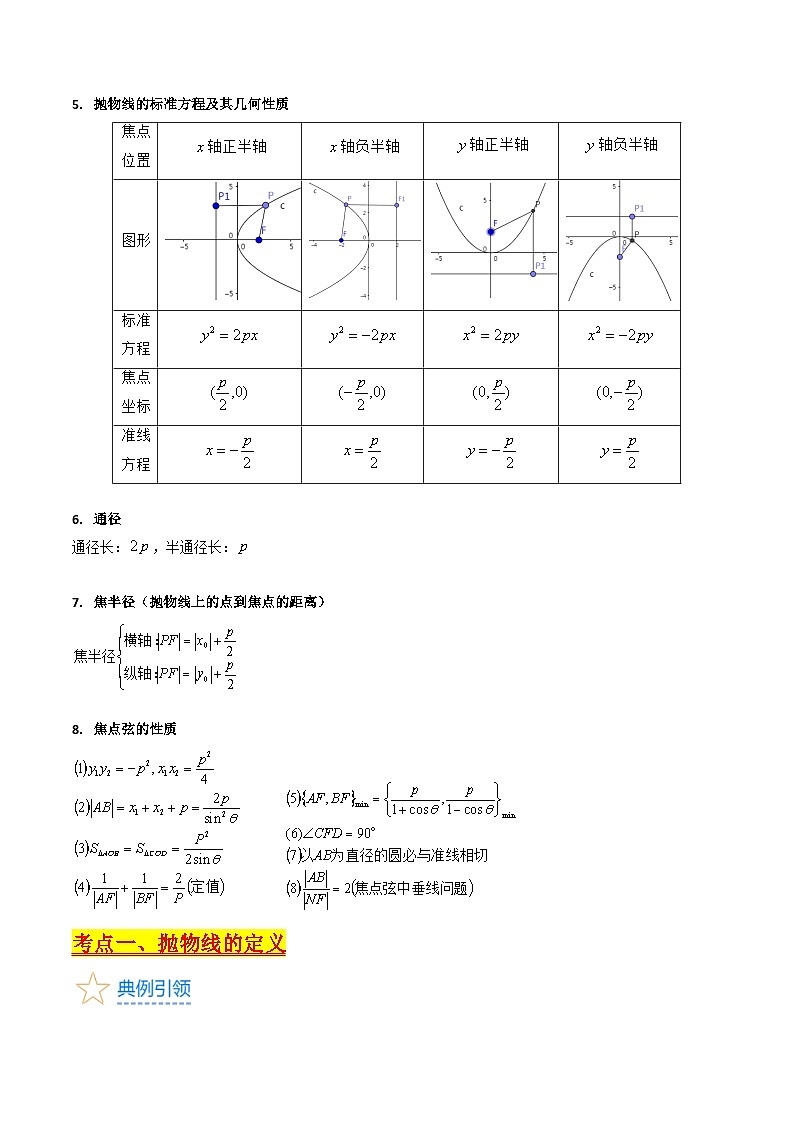
抛物线的标准方程及其几何性质
通径
通径长：，半通径长：
焦半径（抛物线上的点到焦点的距离）
焦点弦的性质

考点一、抛物线的定义
1．（2023·全国·高三专题练习）已知点，直线，若动点到的距离等于，则点的轨迹是（ ）
A．椭圆B．双曲线
C．抛物线D．直线
2．（2023·北京·高考）已知抛物线的焦点为，点在上．若到直线的距离为5，则（ ）
A．7B．6C．5D．4
3．（2023·江西·校联考三模）设圆与y轴交于A，B两点（A在B的上方），过B作圆O的切线l，若动点P到A的距离等于P到l的距离，则动点P的轨迹方程为（ ）
A．B．C．D．
4．（2023·全国·高三专题练习）复数（为虚数单位）在复平面内对应点，则下列为真命题的是（ ）．
A．若，则点在圆上
B．若，则点在椭圆上
C．若，则点在双曲线上
D．若，则点在抛物线上
5．（2023·江苏常州·校考一模）（多选）已知定圆A的半径为1，圆心A到定直线l的距离为d，动圆C与圆A和直线l都相切，圆心C的轨迹为如图所示的两条抛物线，记这两抛物线的焦点到对应准线的距离分别为，，则（ ）
A．B．C．D．
1．（2023·全国·高三专题练习）已知动圆M与直线y=2相切，且与定圆 外切，则动圆圆心M的轨迹方程为（ ）
A． B．C． D．
2．（2023·全国·高三专题练习）已知点，点B为直线上的动点，过点B作直线的垂线l，且线段的中垂线与l交于点P．
(1)求点P的轨迹的方程；
(2)设与x轴交于点M，直线与交于点G（异于P），求四边形面积的最小值．
3．（2023·全国·高三专题练习）已知动点到定点的距离比到直线的距离小2，设动点的轨迹为曲线.
(1)求曲线的方程；
(2)设是轴上的点，曲线与直线交于，且的面积为，求点的坐标.
4．（2023·全国·高三专题练习）已知动圆过定点，且与直线相切．
(1)求动圆圆心的轨迹的方程；
(2)过点且斜率为的两条直线分别交曲线于点，点分别是线段的中点，若，求点到直线的距离的最大值．
5．（2023·全国·高三专题练习）已知点，动点M在直线上，过点M且垂直于x轴的直线与线段的垂直平分线交于点P，记点P的轨迹为曲线C．
(1)求曲线C的方程；
(2)已知圆的一条直径为，延长分别交曲线C于两点，求四边形面积的最小值．
考点二、抛物线的标准方程
1．（2021·全国·统考高考真题）抛物线的焦点到直线的距离为，则（ ）
A．1B．2C．D．4
2．（2023·四川成都·四川省成都列五中学校考三模）若抛物线上的点P到焦点的距离为8，到轴的距离为6，则抛物线的标准方程是（ ）
A．B．C．D．
3．（2023·海南省直辖县级单位·嘉积中学校考三模）（多选）设抛物线：的焦点为，点在抛物线上，点，若，且，则抛物线的方程可以为（ ）
A．B．C．D．
1．（2023·辽宁辽阳·统考二模）已知抛物线的焦点为在抛物线上，且，则（ ）
A．2B．4C．8D．12
2．（2023·广东梅州·统考三模）已知抛物线的焦点为，点，线段与抛物线相交于点，若抛物线在点处的切线与直线垂直，则抛物线的方程为（ ）
A．B．C．D．
3．（2022·全国·统考高考真题）设抛物线的焦点为F，点，过F的直线交C于M，N两点．当直线MD垂直于x轴时，．
(1)求C的方程；
(2)设直线与C的另一个交点分别为A，B，记直线的倾斜角分别为．当取得最大值时，求直线AB的方程．
考点三、抛物线的几何性质
1．（2023·天津和平·统考一模）抛物线的焦点为，其准线与双曲线的渐近线相交于两点，若的周长为，则（ ）
A．2B．C．8D．4
2．（2023·全国·模拟预测）已知抛物线的焦点为F，准线为l，与x轴平行的直线与l和抛物线C分别交于A，B两点，且，则（ ）
A．2B．C．D．4
3．（2023·江苏常州·江苏省前黄高级中学校考模拟预测）已知点是抛物线上的一点，，是抛物线的焦点，且，则的值为（ ）
A．1B．2C．D．
4．（2023·福建厦门·厦门一中校考模拟预测）已知抛物线：的焦点为，点为上一点，为靠近点的三等分点，若，则点的纵坐标为（ ）
A．2B．4C．6D．8
5．（2023·河北唐山·迁西县第一中学校考二模）已知抛物线，直线与C的一个交点为M，F为抛物线C的焦点，O为坐标原点，若，则（ ）
A．B．C．D．
6．（2023·湖南常德·常德市一中校考模拟预测）（多选）已知抛物线经过点，其焦点为，过点的直线与抛物线交于点，，设直线，的斜率分别为，，则（ ）
A． B．
C．D．
7．（2023·湖北襄阳·襄阳四中校考模拟预测）（多选）已知抛物线的焦点为F，准线与x轴的交点为C，过点C的直线l与抛物线E交于A，B两点（点A和点C在点B的两侧），则下列命题正确的是（ ）
A．若BF为的中线，则
B．若BF为的角平分线，则
C．存在直线l，使得
D．对于任意直线l，都有
8．（2023·湖北武汉·统考模拟预测）已知抛物线的焦点为，准线与轴的交点为，过点的直线与抛物线交于，两点，若，则 ．
1．（2023·甘肃陇南·统考一模）设为抛物线的焦点，为抛物线上一点，若，则点的横坐标为 ．
2．（2023·河南·校联考模拟预测）已知抛物线的焦点为F，准线为l，A，B为C上两点，且均在第一象限，过A，B作l的垂线，垂足分别为D，E.若，，则的外接圆面积为（ ）.
A．B．C．D．
3．（2023·河南濮阳·濮阳一高校考模拟预测）焦点为的抛物线上有一点，为坐标原点，则满足的点的坐标为（ ）
A．B．C．D．
4．（2023·河南郑州·统考模拟预测）已知抛物线，F为抛物线的焦点，P为抛物线上一点，过点P作PQ垂直于抛物线的准线，垂足为Q，若，则△PFQ的面积为（ ）
A．4B．C．D．
5．（2023·广西南宁·南宁二中校联考模拟预测）已知抛物线C的焦点F在x轴的正半轴上，且焦点到准线的距离为2，过点F且倾斜角为的直线交抛物线C于A，B两点，则（ ）．
A．B．5C．D．2
6．（2023·浙江·校联考模拟预测）设抛物线的焦点为，过点作直线与抛物线交于两点且，则的值为（ ）
A．B．C．D．
7．（2023·山东淄博·山东省淄博实验中学校考三模）已知抛物线的焦点为，直线与抛物线交于两点，是线段的中点，过作轴的垂线交抛物线于点，则下列判断不正确的是（ ）
A．若过点，则的准线方程为B．若过点，则
C．若，则D．若，则点的坐标为
8．（2023·吉林通化·梅河口市第五中学校考模拟预测）（多选）已知点A是抛物线上的动点，为坐标原点，为焦点，，且三点顺时针排列，则（ ）
A．当点在轴上时，
B．当点在轴上时，点A的坐标为
C．当点A与点关于轴对称时，
D．若，则点A与点关于轴对称
考点四、抛物线中的最值问题
1．（2023·四川成都·校联考二模）已知点是抛物线的焦点，点，且点为抛物线上任意一点，则的最小值为（ ）
A．5B．6C．7D．8
2．（2023·广东深圳·深圳中学校考模拟预测）已知为抛物线的焦点，直线与交于，两点，则的最小值是（ ）
A．10B．9C．8D．5
3．（2023·陕西商洛·统考一模）已知F为抛物线的焦点，P为该抛物线上的动点，点，则的最大值为（ ）
A．B．C．2D．
4．（2023·全国·模拟预测）已知A，B是拋物线上两个不同的点，F为拋物线的焦点，G为的重心．若，则的最小值为 ．
5．（2023·广东深圳·深圳中学校联考模拟预测）已知点M为抛物线上的动点，点N为圆上的动点，则点M到y轴的距离与点M到点N的距离之和最小值为 ..
6．（2023·河南开封·开封高中校考模拟预测）已知抛物线，P为C上一点，，，当最小时，点P到坐标原点的距离为（ ）
A．B．C．D．8
7．（2023·山西朔州·怀仁市第一中学校校考二模）已知抛物线的焦点为F，点A，B在抛物线上．若，则当取得最大值时， ．
8．（2023·广西南宁·南宁三中校考模拟预测）已知斜率为的直线过抛物线的焦点，且与该抛物线交于两点，若为该抛物线上一点，为圆上一点，则的最小值为 .
9．（2023·河北·校联考一模）（多选）抛物线的焦点为，为抛物线上的动点，若点不在抛物线上，且满足的最小值为，则的值可以为（ ）
A．B．3C．D．
1．（2023·江苏无锡·校联考三模）已如，是抛物线上的动点（异于顶点），过作圆的切线，切点为，则的最小值为 .
2．（2023·山东潍坊·统考模拟预测）已知抛物线，其焦点为F，PQ是过点F的一条弦，定点A的坐标是，当取最小值时，则弦PQ的长是 .
3．（2023·黑龙江齐齐哈尔·统考二模）已知抛物线的焦点为，为上的动点，为圆上的动点，设点到轴的距离为，则的最小值为（ ）
A．B．C．D．
4．（2023·江苏南通·统考模拟预测）已知点是抛物线上的动点，则的最小值为 .
5．（2023·江西南昌·校联考模拟预测）已知抛物线，圆，P为E上一点，Q为C上一点，则的最小值为（ ）
A．2B．C．D．3
6．（2023·全国·模拟预测）已知，是抛物线上两个不同的点，为抛物线的焦点，为的重心.若，则的最小值为（ ）
A．B．C．D．
7．（2023·浙江·校联考二模）已知直线和直线，拋物线上一动点到直线直线的距离之和的最小值是（ ）
A．2B．3C．D．
8．（2023·江西九江·统考一模）已知点分别是抛物线和圆上的动点，点到直线的距离为，则的最小值为 ．
9．（2023·广东茂名·统考二模）（多选）阿波罗尼奥斯是古希腊著名的数学家，与欧几里得、阿基米德齐名，他的著作《圆锥曲线论》是古代世界光辉的科学成果，它将圆锥曲线的性质网罗殆尽，几乎使后人没有插足的余地.其中给出了抛物线一条经典的光学性质：从焦点发出的光线，经过抛物线上的一点反射后，反射光线平行于抛物线的轴.此性质可以解决线段和的最值问题，已知抛物线，是抛物线上的动点，焦点，，下列说法正确的是（ ）

A．的方程为B．的方程为
C．的最小值为D．的最小值为
考点五、抛物线的简单应用
1．（2023·广西玉林·统考二模）南宋晚期的龙泉窑粉青釉刻花斗笠盏如图1所示，忽略杯盏的厚度，这只杯盏的轴截面如图2所示，其中光滑的曲线是抛物线的一部分，已知杯盏盛满茶水时茶水的深度为3cm，则该抛物线的焦点到准线的距离为（ ）
A．B．C．D．
2．（2023·湖北·统考模拟预测）随着科技的进步，我国桥梁设计建设水平不断提升，创造了多项世界第一，为经济社会发展发挥了重要作用.下图是某景区内的一座抛物线拱形大桥，该桥抛物线拱形部分的桥面跨度为10米，拱形最高点与水面的距离为6米，为增加景区的夜晚景色，景区计划在拱形桥的焦点处悬挂一闪光灯，则竖直悬挂的闪光灯距离水面的距离为（ ）（结果精确到0.01）
A．4.96B．5.06C．4.26D．3.68
3．（2023·江苏南通·校联考模拟预测）如图1所示，抛物面天线是指由抛物面（抛物线绕其对称轴旋转形成的曲面）反射器和位于焦点上的照射器（馈源，通常采用喇叭天线）组成的单反射面型天线，广泛应用于微波和卫星通讯等领域，具有结构简单、方向性强、工作频带宽等特点．图2是图1的轴截面，A，B两点关于抛物线的对称轴对称，F是抛物线的焦点，∠AFB是馈源的方向角，记为，焦点F到顶点的距离f与口径d的比值称为抛物面天线的焦径比，它直接影响天线的效率与信噪比等．如果某抛物面天线馈源的方向角满足，，则其焦径比为（ ）
A．B．C．D．
1．（2023·河南·襄城高中校联考三模）清代青花瓷盖碗是中国传统茶文化的器物载体，具有“温润”“淡远”“清新”的特征．如图，已知碗体和碗盖的内部均近似为抛物线形状，碗盖深为，碗盖口直径为，碗体口直径为，碗体深，则盖上碗盖后，碗盖内部最高点到碗底的垂直距离为（碗和碗盖的厚度忽略不计）（ ）

A．B．C．D．
2．（2023·海南省直辖县级单位·校联考二模）中国古代桥梁的建筑艺术，有不少是世界桥梁史上的创举，充分显示了中国劳动人民的非凡智慧．一个抛物线型拱桥，当水面离拱顶2m时，水面宽8m．若水面下降1m，则水面宽度为（ ）
A． mB． mC． mD．12 m
3．（2023·河北张家口·统考二模）探照灯､汽车前灯的反光曲面､手电筒的反光镜面､太阳灶的镜面等都是抛物镜面.灯泡放在抛物线的焦点位置，通过镜面反射就变成了平行光束，如图所示，这就是探照灯､汽车前灯､手电筒的设计原理.已知某型号探照灯反射镜的纵断面是抛物线的一部分，光源位于抛物线的焦点处，灯口直径是，灯深，则光源到反射镜顶点的距离为（ ）
A．B．C．D．
【基础过关】
一、单选题
1．（2023·湖南娄底·统考模拟预测）已知抛物线上的点到其焦点的距离为4，则（ ）
A．1B．2C．3D．4
2．（2023·浙江绍兴·统考模拟预测）设抛物线的焦点为，若点在抛物线上，且，则（ ）
A．1B．2C．4D．8
3．（2023·广东梅州·大埔县虎山中学校考模拟预测）已知是抛物线上一点，为抛物线的焦点，点，若，则的面积为（ ）
A．B．C．D．
4．（2023·湖北十堰·统考二模）已知抛物线C：的焦点为F，抛物线C的准线与坐标轴相交于点P，点，且的面积为2，若Q是抛物线C上一点，则周长的最小值为（ ）．
A．B．C．D．
二、多选题
5．（2023·辽宁辽阳·统考一模）若抛物线上一点到焦点的距离是它到直线的距离的8倍，则该抛物线的焦点到准线的距离可以为（ ）
A．B．C．D．
6．（2023·江苏常州·校考二模）如图，已知抛物线，过抛物线焦点的直线自上而下，分别交抛物线与圆于四点，则（ ）
A．B．
C．D．
三、填空题
7．（2023·山东青岛·统考三模）已知椭圆的长轴长为，它的一个焦点与抛物线的焦点重合，则椭圆的标准方程为 ．
8．（2023·福建泉州·统考模拟预测）已知抛物线的焦点为，过点的直线与交于不同的两点，.若，则 .
9．（2023·江苏淮安·江苏省郑梁梅高级中学校考模拟预测）已知抛物线的的准线与轴交于点，，是的焦点，是上一点，，则 .
10．（2023·河北衡水·河北衡水中学校考模拟预测）抛物线绕其顶点顺时针旋转之后，得到的图像正好对应抛物线，则 .
【能力提升】
一、单选题
1．（2023·青海西宁·统考二模）已知点是抛物线上的一点,点是圆上的一点,为坐标原点,则的最大值为( )
A．B．C．D．
2．（2023·全国·模拟预测）已知抛物线：的焦点为，动点为抛物线上一点（与轴不垂直），过点作轴于点，作交轴于点，若（），则实数的最大值为（ ）
A．3B．6C．9D．12
3．（2023·湖南长沙·长沙市明德中学校考三模）已知抛物线的焦点为 ，准线为，为上一点，，垂足为，与轴交点为，若，且的面积为，则的方程为（ ）
A．B．C．D．
4．（2023·全国·模拟预测）已知是抛物线的焦点，点A，B在抛物线上，且的重心坐标为，则（ ）
A．B．6C．D．
5．（2023·重庆万州·重庆市万州第二高级中学校考三模）已知点F为抛物线的焦点，，点M为抛物线上一动点，当最小时，点M恰好在以A，F为焦点的双曲线C上，则双曲线C的渐近线斜率的平方是（ ）
A．B．C．D．
6．（2023·湖南岳阳·湖南省平江县第一中学校考模拟预测）已知抛物线，焦点为F，点M是抛物线C上的动点，过点F作直线的垂线，垂足为P，则的最小值为（ ）
A．B．C．D．3
7．（2023·浙江杭州·统考模拟预测）已知抛物线的焦点为F，直线l过焦点F与C交于A，B两点，以为直径的圆与y轴交于D，E两点，且，则直线l的方程为（ ）
A．B．
C．D．
二、多选题
8．（2023·湖北黄冈·浠水县第一中学校考三模）已知抛物线C：的焦点为F，P，Q为C上两点，则下列说法正确的是（ ）
A．若，则的最小值为4
B．若，记，则
C．过点与C只有一个公共点的直线有且仅有两条
D．以PQ为直径的圆与C的准线相切，则直线PQ过F
9．（2023·山东济宁·嘉祥县第一中学统考三模）已知抛物线的焦点为，准线为，过的直线与抛物线交于、两点，为线段中点，、、分别为、、在上的射影，且，则下列结论中正确的是（ ）
A．的坐标为B．
C．、、、四点共圆D．直线的方程为
10．（2023·江西·校联考模拟预测）已知抛物线的焦点为，定点和动点，都在抛物线上，且（其中为坐标原点）的面积为3，则下列说法正确的是（ ）
A．抛物线的标准方程为
B．设点是线段的中点，则点的轨迹方程为
C．若（点在第一象限），则直线的倾斜角为
D．若弦的中点的横坐标2，则弦长的最大值为7
三、填空题
11．（2023·广西南宁·南宁二中校考模拟预测）已知点，点P在抛物线上运动，F是抛物线的焦点，连接PF并延长与圆交于点B，则的最小值是 .
12．（2023·黑龙江大庆·统考三模）古希腊数学家阿波罗尼奥斯与欧几里得、阿基米德齐名，他的著作《圆锥曲线论》是古代数学光辉的科学成果．他发现“平面内到两个定点A，B的距离之比为定值（且）的点的轨迹是圆”，人们将这样的圆称为阿波罗尼斯圆，简称阿氏圆．在平面直角坐标系中，已知，，，Q为抛物线上的动点，点Q在直线上的射影为H，M为圆上的动点，若点P的轨迹是到A，B两点的距离之比为的阿氏圆，则的最小值为 ．
【真题感知】
一、单选题
1．（2022·全国·统考高考真题）设F为抛物线的焦点，点A在C上，点，若，则（ ）
A．2B．C．3D．
2．（2020·全国·统考高考真题）已知A为抛物线C:y2=2px（p>0）上一点，点A到C的焦点的距离为12，到y轴的距离为9，则p=（ ）
A．2B．3C．6D．9
3．（2020·北京·统考高考真题）设抛物线的顶点为，焦点为，准线为．是抛物线上异于的一点，过作于，则线段的垂直平分线（ ）．
A．经过点B．经过点
C．平行于直线D．垂直于直线
二、多选题
4．（2022·全国·统考高考真题）已知O为坐标原点，点在抛物线上，过点的直线交C于P，Q两点，则（ ）
A．C的准线为B．直线AB与C相切
C．D．
5．（2022·全国·统考高考真题）已知O为坐标原点，过抛物线焦点F的直线与C交于A，B两点，其中A在第一象限，点，若，则（ ）
A．直线的斜率为B．
C．D．
6．（2023·全国·统考高考真题）设O为坐标原点，直线过抛物线的焦点，且与C交于M，N两点，l为C的准线，则（ ）．
A．B．
C．以MN为直径的圆与l相切D．为等腰三角形
三、填空题
7．（2023·全国·统考高考真题）已知点在抛物线C：上，则A到C的准线的距离为 .
8．（2021·全国·统考高考真题）已知为坐标原点，抛物线：()的焦点为，为上一点，与轴垂直，为轴上一点，且，若，则的准线方程为 .
四、双空题
9．（2021·北京·统考高考真题）已知抛物线的焦点为，点在抛物线上，垂直轴与于点.若，则点的横坐标为 ； 的面积为 ．
五、解答题
10．（2021·全国·统考高考真题）已知抛物线的焦点F到准线的距离为2．
（1）求C的方程;
（2）已知O为坐标原点，点P在C上，点Q满足，求直线斜率的最大值.
11．（2020·全国·统考高考真题）已知椭圆C1：(a>b>0)的右焦点F与抛物线C2的焦点重合，C1的中心与C2的顶点重合．过F且与x轴垂直的直线交C1于A，B两点，交C2于C，D两点，且|CD|=|AB|．
（1）求C1的离心率；
（2）若C1的四个顶点到C2的准线距离之和为12，求C1与C2的标准方程．
不妨设在第一象限，因为椭圆的方程为：，
所以当时，有，因此的纵坐标分别为，；
又因为抛物线的方程为，所以当时，有，
所以的纵坐标分别为，，故，.
由得，即，解得（舍去），.
所以的离心率为.
（2）由（1）知，，故，所以的四个顶点坐标分别为，，，，的准线为.
由已知得，即.
所以的标准方程为，的标准方程为.
【点睛】本题考查了求椭圆的离心率，考查了求椭圆和抛物线的标准方程，考查了椭圆的四个顶点的坐标以及抛物线的准线方程，考查了数学运算能力.
12．（2020·山东·统考高考真题）已知抛物线的顶点在坐标原点，椭圆的顶点分别为，，，，其中点为抛物线的焦点，如图所示.
（1）求抛物线的标准方程；
（2）若过点的直线与抛物线交于，两点，且，求直线的方程.
13．（2021·全国·高考真题）抛物线C的顶点为坐标原点O．焦点在x轴上，直线l：交C于P，Q两点，且．已知点，且与l相切．
（1）求C，的方程；
（2）设是C上的三个点，直线，均与相切．判断直线与的位置关系，并说明理由．
焦点位置
轴正半轴
轴负半轴
轴正半轴
轴负半轴
图形
标准方程
焦点坐标
准线方程