新高考数学一轮复习精品讲练测第9章第03讲 二项式定理（2份，原卷版+解析版）

这是一份新高考数学一轮复习精品讲练测第9章第03讲 二项式定理（2份，原卷版+解析版），文件包含新高考数学一轮复习精品讲练测第9章第03讲二项式定理教师版doc、新高考数学一轮复习精品讲练测第9章第03讲二项式定理学生版doc等2份试卷配套教学资源，其中试卷共90页， 欢迎下载使用。

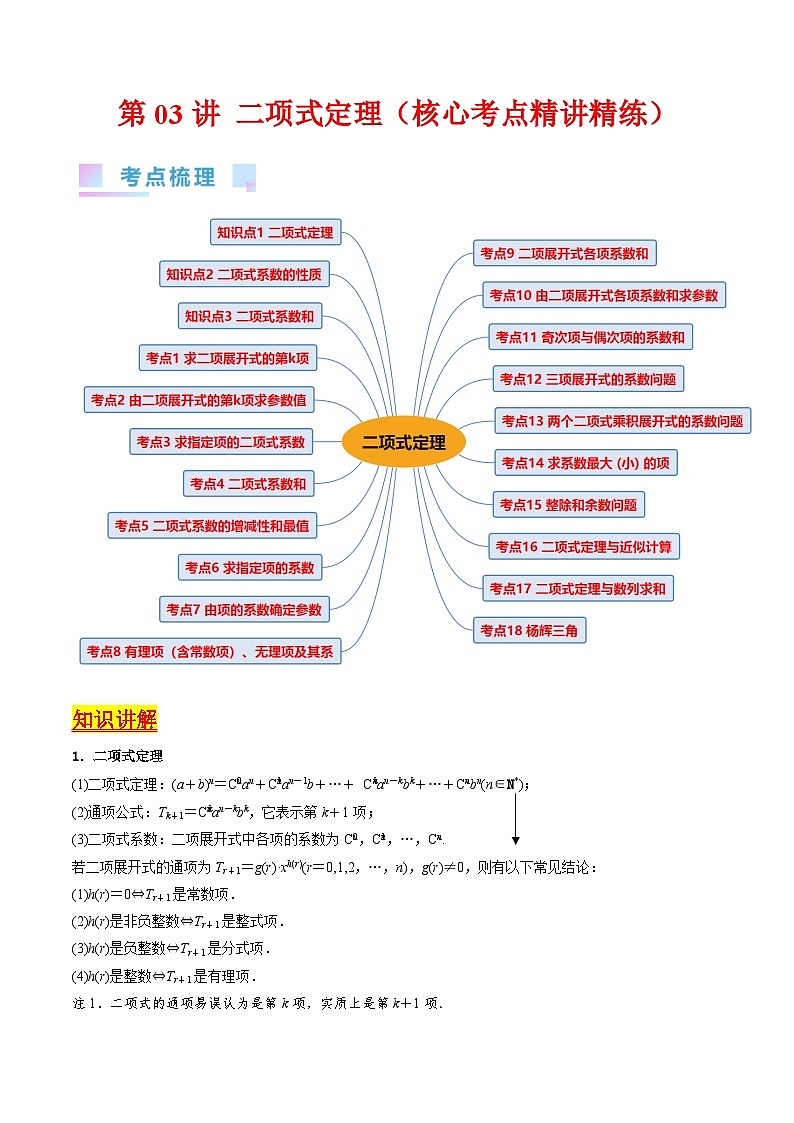
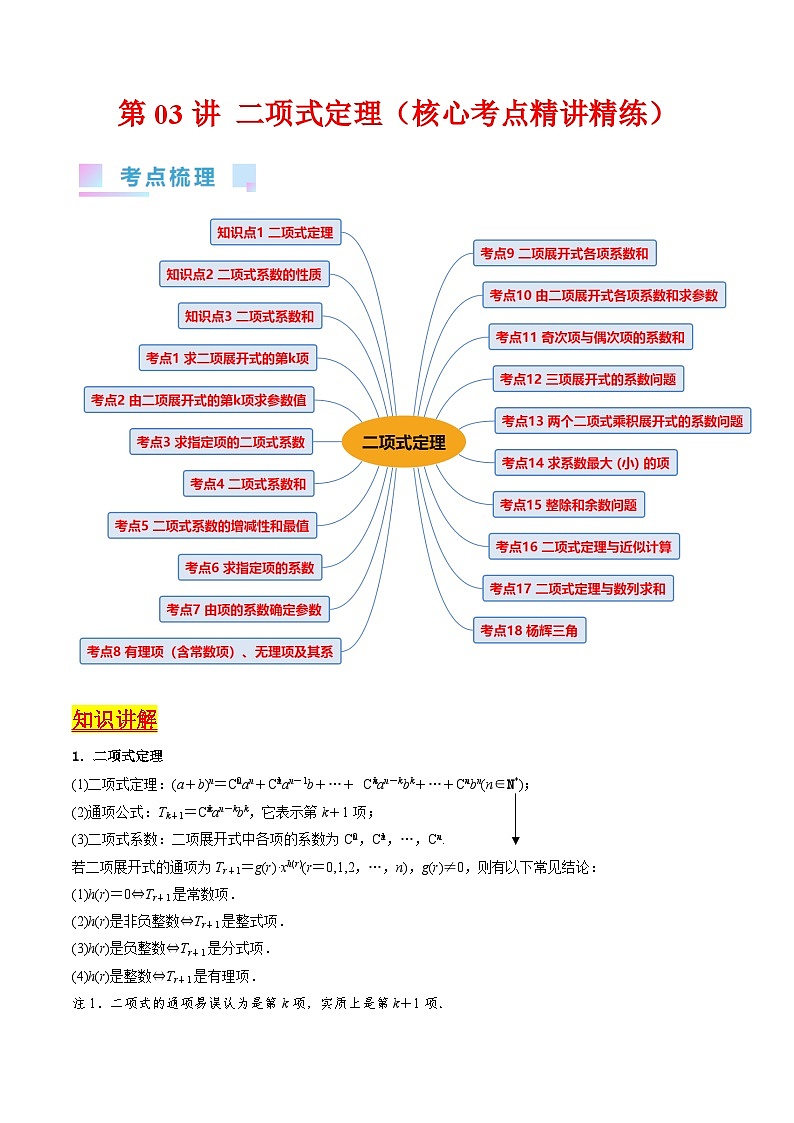
知识讲解
1．二项式定理
(1)二项式定理：(a＋b)n＝Ceq \\al(0,n)an＋Ceq \\al(1,n)an－1b＋…＋ Ceq \\al(k,n)an－kbk＋…＋Ceq \\al(n,n)bn(n∈N*)；
(2)通项公式：Tk＋1＝Ceq \\al(k,n)an－kbk，它表示第k＋1项；
(3)二项式系数：二项展开式中各项的系数为Ceq \\al(0,n)，Ceq \\al(1,n)，…，Ceq \\al(n,n).
若二项展开式的通项为Tr＋1＝g(r)·xh(r)(r＝0,1,2，…，n)，g(r)≠0，则有以下常见结论：
(1)h(r)＝0⇔Tr＋1是常数项．
(2)h(r)是非负整数⇔Tr＋1是整式项．
(3)h(r)是负整数⇔Tr＋1是分式项．
(4)h(r)是整数⇔Tr＋1是有理项．
注1．二项式的通项易误认为是第k项，实质上是第k＋1项．
注2．易混淆二项式中的“项”“项的系数”“项的二项式系数”等概念，注意项的系数是指非字母因数所有部分，包含符号，二项式系数仅指Ceq \\al(k,n)(k＝0,1，…，n)．
二项式系数的性质
二项式系数和
(a＋b)n的展开式的各个二项式系数的和等于2n，即Ceq \\al(0,n)＋Ceq \\al(1,n)＋Ceq \\al(2,n)＋…＋Ceq \\al(k,n)＋…＋Ceq \\al(n,n)＝2n.
二项展开式中，偶数项的二项式系数的和等于奇数项的二项式系数的和，即Ceq \\al(1,n)＋Ceq \\al(3,n)＋Ceq \\al(5,n)＋…＝Ceq \\al(0,n)＋Ceq \\al(2,n)＋Ceq \\al(4,n)＋…＝.
考点一、求二项展开式的第项
1．（2023·河南·校考模拟预测）的展开式中第3项是 .
2．（2023·全国·高三专题练习）在的展开式中，第四项为（ ）
A．160B．C．D．
1．（2023·北京·校考模拟预测）在的二项展开式中，第四项为 ．
2．（2023·全国·高三专题练习）二项式的展开式的常数项为第_____项
A．17B．18C．19D．20
考点二、由二项展开式的第项求参数值
1．（2023·全国·高三专题练习）已知的展开式中第3项是常数项，则（ ）
A．6B．5C．4D．3
2．（2023·浙江绍兴·统考二模）已知的展开式的常数项是第7项，则 .
1．（2023·全国·高三专题练习）若在的展开式中，第4项是常数项，则 ．
2．（2022·贵州校联考模拟预测）已知展开式中第5项为常数项，则n＝ .
考点三、求指定项的二项式系数
1．（山东·统考高考真题）在的二项展开式中，第项的二项式系数是（ ）
A．B．C．D．
2．（2023·四川内江·四川省内江市第六中学校考模拟预测）在二项式的展开式中，项的二项式系数为 ．
3．（2023·宁夏银川·银川一中校考三模）已知的展开式中，第三项和第四项的二项式系数相等，则 .
4．（2022·河北唐山·统考二模）（多选）已知的展开式中第3项与第8项的二项式系数相等，则（ ）
A．B．
C．常数项是672D．展开式中所有项的系数和是-1
1．（2022·北京通州·潞河中学校考三模）在二项式的展开式中，含项的二项式系数为（ ）
A．5B．C．10D．
2．（2023·湖北襄阳·襄阳四中校考模拟预测）的展开式中含项的二项式系数为 .
3．（2022·江苏无锡·统考模拟预测）二项式的展开式中，含项的二项式系数为（ ）
A．84B．56C．35D．21
考点四、二项式系数和
1．（2023·上海浦东新·华师大二附中校考三模）已知（为正整数）的展开式中所有项的二项式系数的和为64，则 .
2．（2022·四川德阳·统考一模）已知二项式的展开式中最后三项的二项式系数和为79,则n = .
1．（2023·河北张家口·统考二模）已知的展开式的各二项式系数的和为64，则常数项为 .（用数字作答）
2．（2023·北京朝阳·二模）已知的展开式中所有项的二项式系数的和为64，则 ，展开式中的系数为 .
考点五、二项式系数的增减性和最值
1．（2023·山西朔州·怀仁市第一中学校校考模拟预测）在的展开式中，二项式系数最大的项的系数为（ ）
A．20B．160C．180D．240
2．（2023·四川绵阳·统考模拟预测）展开式中，只有第4项的二项式系数最大，则n的值为（ ）
A．8B．7C．6D．5
3．（2023·陕西西安·校联考一模）设m为正整数，展开式中二项式系数的最大值为a，展开式中二项式系数的最大值为b，若，则展开式中的常数项为 ．
1．（2023·山东·山东省实验中学校考二模）展开式中二项式系数最大的项的系数为 ．
2．（2023·安徽安庆·安庆一中校考模拟预测）的展开式中二项式系数最大的项是 .
3．（2023·福建泉州·泉州五中校考模拟预测）已知的展开式中，仅有第4项的二项式系数最大，则展开式中第5项是 .
考点六、求指定项的系数
1．（2023·北京·统考高考真题）的展开式中的系数为（ ）．
A．B．C．40D．80
2．（北京·统考高考真题）在的展开式中，的系数为（ ）．
A．B．5C．D．10
3．（2023·浙江嘉兴·统考模拟预测）的展开式中的系数是 ．（用数字作答）
4．（2023·四川成都·校联考模拟预测）已知的展开式中第4项与第5项的二项式系数相等，则展开式中的项的系数为（ ）
A．―4B．84C．―280D．560
1．（2021·天津·统考高考真题）在的展开式中，的系数是 ．
2．（天津·统考高考真题）在的展开式中，的系数是 ．
3．（2023·天津·统考高考真题）在的展开式中，项的系数为 ．
4．（2023·海南省直辖县级单位·嘉积中学校考三模）的展开式中项的系数为 ．（用数字作答）
考点七、由项的系数确定参数
3.1
1．（2023·江苏连云港·校考模拟预测）已知的展开式中的系数是，则 .
2．（2023·江苏淮安·江苏省郑梁梅高级中学校考模拟预测）已知的展开式中一次项系数为，则 .
3．（2023·吉林长春·长春吉大附中实验学校校考模拟预测）已知展开式中的第三项的系数为45，则（ ）
A．B．展开式中所有系数和为
C．二项式系数最大的项为中间项D．含的项是第7项
1．（2023·河北秦皇岛·校联考模拟预测）已知的展开式中的系数为，则实数 ．
2．（2023·辽宁大连·大连八中校考三模）若的二项展开式中的系数是，则实数的值是 ．
3．（2023·河北·统考模拟预测）已知的展开式中含的项的系数为，则（ ）
A．B．C．D．
考点八、有理项（含常数项）、无理项及其系数
1．（2021·北京·统考高考真题）在的展开式中，常数项为 ．
2．（2022·天津·统考高考真题）的展开式中的常数项为 .
1．（2023·湖北·模拟预测）展开式中无理项的个数为（ ）
A．6B．7C．8D．9
2．（2023·四川成都·四川省成都市玉林中学校考模拟预测）在二项式的展开式中，二项式的系数和为256，把展开式中所有的项重新排成一列，有理项都互不相邻的概率为（ ）
A．B．C．D．
1．（全国·统考高考真题）的展开式中常数项是 （用数字作答）．
2．（2023·山东烟台·校联考三模）已知的展开式中共有项，则有理项共 项．（用数字表示）
3．（2023·江苏苏州·苏州中学校考模拟预测）已知的展开式中，仅有第5项的二项式系数最大，则展开式中有理项的个数为 ．
4．（2023·广东惠州·统考一模）已知二项式的展开式中只有第4项的二项式系数最大，现从展开式中任取2项，则取到的项都是有理项的概率为（ ）
A．B．C．D．
考点九、二项展开式各项系数和
1．（2022·浙江·统考高考真题）已知多项式，则 ， ．
2．（2021·浙江·统考高考真题）已知多项式，则 ， .
3．（浙江·统考高考真题）设，则 ； ．
4．（2023·黑龙江哈尔滨·哈尔滨市第四中学校校考模拟预测）若，，则 .
5．（2023·山东日照·三模）（多选）已知，则（ ）
A．B．
C．D．
考点十、由二项展开式各项系数和求参数
1．（2023·河南洛阳·洛阳市第三中学校联考一模）在的展开式中，各项系数的和与各二项式系数的和之比为64，则 ．
2．（2023·河南·襄城高中校联考模拟预测）若的展开式中各项系数之和为1024，则第四项与第五项的系数之比为（ ）
A．B．C．D．
3．（2023·辽宁抚顺·校考模拟预测）（多选）在的展开式中，各项系数的和为1，则（ ）
A．B．展开式中的常数项为
C．展开式中的系数为160D．展开式中无理项的系数之和为
1．（2022·湖北武汉·三模）在展开式中，x的所有奇数次幂项的系数之和为20，则 ．
2．（2023·全国·模拟预测）已知的展开式中各项的系数之和为256，记展开式中的系数为，则 .
3．（2023·河北·统考模拟预测）（多选）已知二项式的展开式中所有项的系数的和为64，则（ ）
A．
B．展开式中的系数为
C．展开式中奇数项的二项式系数的和为32
D．展开式中二项式系数最大的项为
考点十一、奇次项与偶次项的系数和
1．（2022·北京·统考高考真题）若，则（ ）
A．40B．41C．D．
1．（2023·四川南充·四川省南充高级中学校考三模）若，则 .
2．（2023·北京大兴·校考三模）若，则 .
3．（2023·山东·山东省实验中学校联考模拟预测）若，则 .
4．（2023·上海杨浦·复旦附中校考模拟预测）若， 则 .
考点十二、三项展开式的系数问题
1．（2023·河北沧州·校考模拟预测）的展开式中的系数为（ ）
A．B．10C．D．30
2．（2023·江西南昌·校联考模拟预测）在的展开式中，项的系数为（ ）
A．1680B．210C．－210D．－1680
3．（2023·湖北武汉·华中师大一附中校考模拟预测）的展开式中的系数为12，则（ ）
A．B．C．D．
4．（2023·湖北·模拟预测）展开式中无理项的个数为（ ）
A．6B．7C．8D．9
5．（2023·湖北省直辖县级单位·统考模拟预测）已知常数，的二项展开式中项的系数是780，则m的值为 ．
1．（2023·广东汕头·统考三模）展开式中的系数是 .
2．（2023·辽宁·大连二十四中校联考模拟预测）的展开式中的系数为 （用数字作答）．
3．（2023·江苏·金陵中学校联考三模）展开式中的常数项为 .
4．（2023·湖南长沙·长沙市实验中学校考二模）已知二项式的展开式中含的项的系数为，则 ．
5．（2023·福建·校联考模拟预测）展开式中的常数项为 .（用数字做答）
考点十三、两个二项式乘积展开式的系数问题
1．（全国·统考高考真题）的展开式中x3y3的系数为（ ）
A．5B．10
C．15D．20
2．（2022·全国·统考高考真题）的展开式中的系数为 （用数字作答）．
3．（2023·福建龙岩·统考二模）已知的展开式中的系数为21，则 ．
4．（2023·浙江温州·乐清市知临中学校考模拟预测）在的展开式中，x的系数为 ．
5．（2023·安徽亳州·安徽省亳州市第一中学校考模拟预测）展开式中的系数为 .
1．（2023·山西运城·山西省运城中学校校考二模）展开式中的系数是 .
2．（2023·辽宁抚顺·校考模拟预测）在的展开式中，系数最大的项为 .
3．（2023·浙江·校联考模拟预测）的展开式中的系数为 （用数字作答）.
4．（2023·浙江·校联考模拟预测）已知的展开式中常数项为120，则 .
5．（2023·福建厦门·厦门一中校考模拟预测）已知（为常数）的展开式中各项系数之和为，则展开式中的系数为 ．
考点十四、求系数最大 (小) 的项
1．（2023·山东·模拟预测）（多选）的展开式中系数最大的项是（ ）
A．第2项B．第3项C．第4项D．第5项
2．（2023·江西南昌·江西师大附中校考三模）若的展开式中有且仅有第五项的二项式系数最大，则展开式中系数最大的是（ ）
A．第二项B．第三项C．第四项D．第五项
3．（2023·湖北襄阳·襄阳四中校考模拟预测）已知的展开式中前三项的二项式系数和为，则展开式中系数最大的项为第（ ）
A．项B．项C．项D．项
1．（2023·浙江·校考模拟预测）若二项式的展开式中只有第7项的二项式系数最大，若展开式的有理项中第项的系数最大，则（ ）
A．5B．6C．7D．8
2．（2023·上海浦东新·华师大二附中校考模拟预测）的二项展开式中系数最大的项为 .
3．（2023·辽宁抚顺·校考模拟预测）在的展开式中，系数最大的项为 .
考点十五、整除和余数问题
1．（2023·山西·统考模拟预测）除以5的余数是（ ）
A．1B．2C．3D．4
2．（2023·广西南宁·南宁三中校考一模）已知，则！被5除所得余数为（ ）
A．1B．2C．3D．4
3．（2023·江苏盐城·盐城市伍佑中学校考模拟预测）若，则被8整除的余数为（ ）
A．4B．5C．6D．7
4．（2023·江苏无锡·江苏省天一中学校考模拟预测）（多选）若，则（ ）
A．可以被整除
B．可以被整除
C．被27除的余数为6
D．的个位数为6
1．（2023·山西太原·太原五中校考一模）被1000除的余数是（ ）
A．B．C．1D．901
2．（2023·辽宁丹东·统考一模）除以7所得余数为 ．
3．（2023·上海闵行·上海市七宝中学校考三模）若，则被10除所得的余数为 .
4．（2023·江苏扬州·统考模拟预测）若，则被5除所得的余数为 ．
考点十六、二项式定理与近似计算
1．（2022·全国·高三专题练习）的计算结果精确到个位的近似值为
A．106B．107C．108D．109
2．（全国·高三专题练习）求的近似值．(精确到两位小数)
3．（2023·全国·高三专题练习）二项式定理，又称牛顿二项式定理，由艾萨克·牛顿提出.二项式定理可以推广到任意实数次幂，即广义二项式定理：
对于任意实数，
当比较小的时候，取广义二项式定理展开式的前两项可得：，并且的值越小，所得结果就越接近真实数据.用这个方法计算的近似值，可以这样操作：
.
用这样的方法，估计的近似值约为（ ）
A．2.922B．2.926C．2.928D．2.930
1．（2023·全国·高三专题练习）用二项式定理估算 .（精确到0.001）
2．（2023·全国·高三专题练习）利用二项式定理计算，则其结果精确到0.01的近似值是（ ）
A．1.23B．1.24C．1.33D．1.34
3．（2022·全国·高三专题练习） （小数点后保留三位小数）．
考点十七、二项式定理与数列求和
1．（2023·全国·高三专题练习）已知，则（ ）
A．-2B．-1C．0D．2
2．（2022·重庆永川·重庆市永川北山中学校校考模拟预测）已知，则（ ）
A．B．
C．D．
3．（2023·全国·高三专题练习）已知等差数列，对任意都有成立，则数列的前项和 ．
1．（2022·全国·高三专题练习）设是正整数，化简 .
2．（2023秋·重庆·高三重庆一中校考开学考试）已知，则 .
3．（2023·全国·高三对口高考）已知数列的通项公式为．求的值．
考点十八、杨辉三角
1．（2023·全国·高三专题练习）我国南宋数学家杨辉1261年所著的《详解九章算法》一书里出现了如图所示的表，即杨辉三角，这是数学史上的一个伟大成就在“杨辉三角”中，第n行的所有数字之和为，若去除所有为1的项，依次构成数列2，3，3，4，6，4，5，10，10，5，...，则此数列的前34项和为（ ）

A．959B．964C．1003D．1004
2．（2023·全国·高三专题练习）杨辉是我国古代数学史上一位著述丰富的数学家，著有《详解九章算法》《日用算法》和《杨辉算法》.杨辉三角的发现要比欧洲早500年左右，由此可见我国古代数学的成就是非常值得中华民族自豪的.杨辉三角本身包含了很多有趣的性质，利用这些性质，可以解决很多数学问题，如开方、数列等.
我们借助杨辉三角可以得到以下两个数列的和.
；
若杨辉三角中第三斜行的数：1，3，6，10，15，…构成数列，则关于数列叙述正确的是（ ）
A．B．
C．数列的前n项和为D．数列的前n项和为
1．（2023·全国·高三专题练习）（多选）“杨辉三角”是二项式系数在三角形中的一种几何排列，在中国南宋数学家杨辉1261年所著的《详解九章算法》一书中就有出现.如图所示，在“杨辉三角”中，除每行两边的数都是1外，其余每个数都是其“肩上”的两个数之和，例如第4行的6为第3行中两个3的和.则下列命题中正确的是（ ）
A．
B．在第2022行中第1011个数最大
C．记“杨辉三角”第行的第i个数为，则
D．第34行中第15个数与第16个数之比为
6．（2023·全国·高三专题练习）（多选）将杨辉三角中的每一个数都换成，得到如图所示的分数三角形，称为莱布尼茨三角形．莱布尼茨三角形具有很多优美的性质，如从第0行开始每一个数均等于其“脚下”两个数之和，如果，那么下面关于莱布尼茨三角形的结论正确的是（ ）
A．当是偶数时，中间的一项取得最大值，当是奇数时，中间的两项相等，且同时取得最大值
B．
C．
D．
1．（2023·全国·高三专题练习）如图给出的三角形数阵，图中虚线上的数、、、、，依次构成数列，则 .
2．（2023·全国·高三专题练习）“杨辉三角”是中国古代数学文化的瑰宝之一，它揭示了二项式展开式中的组合数在三角形数表中的一种几何排列规律，如图所示，则下列关于“杨辉三角”的结论正确的是（ ）
杨辉三角
A．在第10行中第5个数最大
B．第2023行中第1011个数和第1012个数相等
C．
D．第6行的第7个数、第7行的第7个数及第8行的第7个数之和等于9行的第8个数
3．（2023·全国·高三专题练习）（多选）杨辉三角形，又称贾宪三角形，是二项式系数（，且）在三角形中的一种几何排列，北宋人贾宪约1050年首先使用“贾宪三角”进行高次开方运算，南宋时期杭州人杨辉在他1261年所著的《详解九章算法》一书中，辑录了如下图所示的三角形数表，称之为“开方作法本源”图，并说明此表引自11世纪前半贾宪的《释锁算术》，并绘画了“古法七乘方图”，故此，杨辉三角又被称为“贾宪三角”，杨辉三角形的构造法则为：三角形的两个腰都是由数字1组成的，其余的数都等于它肩上的两个数字相加.根据以上信息及二项式定理的相关知识分析，下列说法中正确的是（ ）
A．
B．当且时，
C．为等差数列
D．存在，使得为等差数列
4．（2023·全国·高三专题练习）（多选）如图给出下列一个由正整数组成的三角形数阵，该三角形数阵的两腰分别是一个公差为的等差数列和一个公差为的等差数列，每一行是一个公差为的等差数列．我们把这个数阵的所有数从上到下，从左到右依次构成一个数列：、、、、、、、、、、，其前项和为，则下列说法正确的有（ ）（参考公式：）
A．B．第一次出现是
C．在中出现了次D．
【基础过关】
一、单选题
1．（2023·湖北襄阳·襄阳四中校考模拟预测）的展开式中的常数项是（ ）
A．B．C．250D．240
二、多选题
2．（2023·云南保山·统考二模）已知二项式的展开式中各项系数之和是128，则下列说法正确的有（ ）
A．展开式共有7项
B．所有二项式系数和为128
C．二项式系数最大的项是第4项
D．展开式的有理项共有4项
3．（2023·吉林白山·抚松县第一中学校考模拟预测）已知，则下列结论正确的是（ ）
A．B．展开式中各项的系数最大的是
C．D．
三、填空题
4．（2023·山东潍坊·三模）已知,则 .（用数字作答）
5．（2023·天津和平·耀华中学校考二模）已知的展开式中各项系数和为243，则展开式中常数项为 ．
6．（2023·陕西西安·校考模拟预测）二项式的展开式中含x的正整数指幂的项数是 .
7．（2023·广西·校联考模拟预测）若，那么的值为 ．
8．（2023·甘肃定西·统考模拟预测）若的展开式中x的系数与的系数相等，则实数a＝ ．
9．（2023·贵州遵义·统考三模）在的展开式中，的系数为 （用数字作答）.
10．（2023·上海·统考模拟预测）的展开式中，常数项为 .
【能力提升】
一、单选题
1．（2023·江西·江西省丰城中学校联考模拟预测）已知，则在的展开式中，含的系数为（ ）
A．480B．C．240D．
2．（2023·江西·校联考二模）若，则（ ）
A．B．48C．28D．
3．（2023·浙江金华·浙江金华第一中学校考模拟预测）已知，则的值为（ ）
A．B．0C．1D．2
4．（2023·甘肃·模拟预测）“杨辉三角”是中国古代数学文化的瑰宝之一，它揭示了二项式展开式中的组合数在三角形数表中的一种几何排列规律，如图所示，则下列关于“杨辉三角”的结论错误的是（ ）
A．第6行的第7个数、第7行的第7个数及第8行的第7个数之和等于第9行的第8个数
B．第2023行中第1012个数和第1013个数相等
C．记“杨辉三角”第行的第个数为，则
D．第34行中第15个数与第16个数之比为
二、多选题
5．（2023·湖北·统考模拟预测）若，则（ ）
A．
B．
C．
D．
6．（2023·河北·统考模拟预测）已知．则（ ）
A．B．
C．D．
三、填空题
7．（2023·浙江·校联考模拟预测）已知函数，设，则 ．
8．（2023·江西九江·统考三模）展开式中，的系数为 ．
9．（2023·山东潍坊·统考模拟预测）若，则 ．
10．（2023·福建龙岩·福建省龙岩第一中学校考模拟预测）在的展开式中，项的系数为 ．
【真题感知】
一、单选题
1．（浙江·高考真题）展开式中的常数项是（ ）
A．B．36C．D．84
2．（重庆·高考真题）若展开式中含项的系数等于含x项的系数的8倍，则n等于（ ）
A．5B．7C．9D．11
3．（重庆·高考真题）若的展开式中前三项的系数成等差数列,则展开式中项的系数为（ ）
A．6B．7C．8D．9
4．（山东·高考真题）如果的展开式中各项系数之和为128，则展开式中的系数是（ ）
A．7B．－7C．21D．－21
5．（全国·高考真题）二项式的展开式中系数为有理数的项共有（ ）
A．6项B．7项C．8项D．9项
6．（重庆·高考真题）若展开式中含项的系数与含项的系数之比为，则n等于（ ）
A．4B．6C．8D．10
7．（江西·高考真题）在的二项展开式中，若常数项为60，则n等于（ ）
A．3B．6C．9D．12
8．（浙江·高考真题）若多项式，则 （ ）
A．9B．10C．-9D．-10
9．（山东·高考真题）已知的展开式中第三项与第五项的系数之比为，其中，则展开式中常数项是（ ）
A．B．C．D．45
10．（重庆·高考真题）若展开式的二项式系数之和为64,则展开式的常数项为
A．10B．20C．30D．120
二、填空题
11．（北京·高考真题）若展开式的各项系数之和为32，则 ，其展开式中的常数项为 ．（用数字作答）
12．（全国·高考真题）的二项展开式中，的系数与的系数之差为 .
13．（广东·高考真题）的展开式中， 的系数是 (用数字作答).
14．（安徽·高考真题）设，则 .
15．（湖南·高考真题）展开式的常数项为 ．（用数字作答）
16．（上海·统考高考真题）在的展开式中，项的系数为 （结果用数值表示）．
17．（天津·高考真题）的二项展开式中，的系数是 .(用数字作答)
18．（安徽·高考真题）已知(1－x)5＝a0＋a1x＋a2x2＋a3x3＋a4x4＋a5x5，则(a0＋a2＋a4)(a1＋a3＋a5)的值等于 ．
19．（全国·高考真题）已知a为实数，展开式中的系数是，则 ．
20．（辽宁·高考真题）展开式中含有x的整数次幂的项的系数之和为 ．（用数字作答）
性质
内容
对称性
与首末两端等距离的两个二项式系数相等，即
增减性
当k＜eq \f(n＋1,2)时，二项式系数逐渐增大；
当k＞eq \f(n＋1,2)时，二项式系数逐渐减小
最大值
当n是偶数时，中间一项eq \b\lc\(\rc\)(\a\vs4\al\c1(第\f(n,2)＋1项))的二项式系数最大，最大值为；
当n是奇数时，中间两项eq \b\lc\(\rc\)(\a\vs4\al\c1(第\f(n－1,2)＋1项和第\f(n＋1,2)＋1项))的二项式系数相等，且同时取得最大值，最大值为或