人教版数学九下期末复习讲练专项07 相似三角形-一线三等角模型综合应用（2份，原卷版+解析版）

这是一份人教版数学九下期末复习讲练专项07 相似三角形-一线三等角模型综合应用（2份，原卷版+解析版），文件包含人教版数学九下期末复习讲练专项07相似三角形-一线三等角模型综合应用原卷版doc、人教版数学九下期末复习讲练专项07相似三角形-一线三等角模型综合应用解析版doc等2份试卷配套教学资源，其中试卷共39页， 欢迎下载使用。

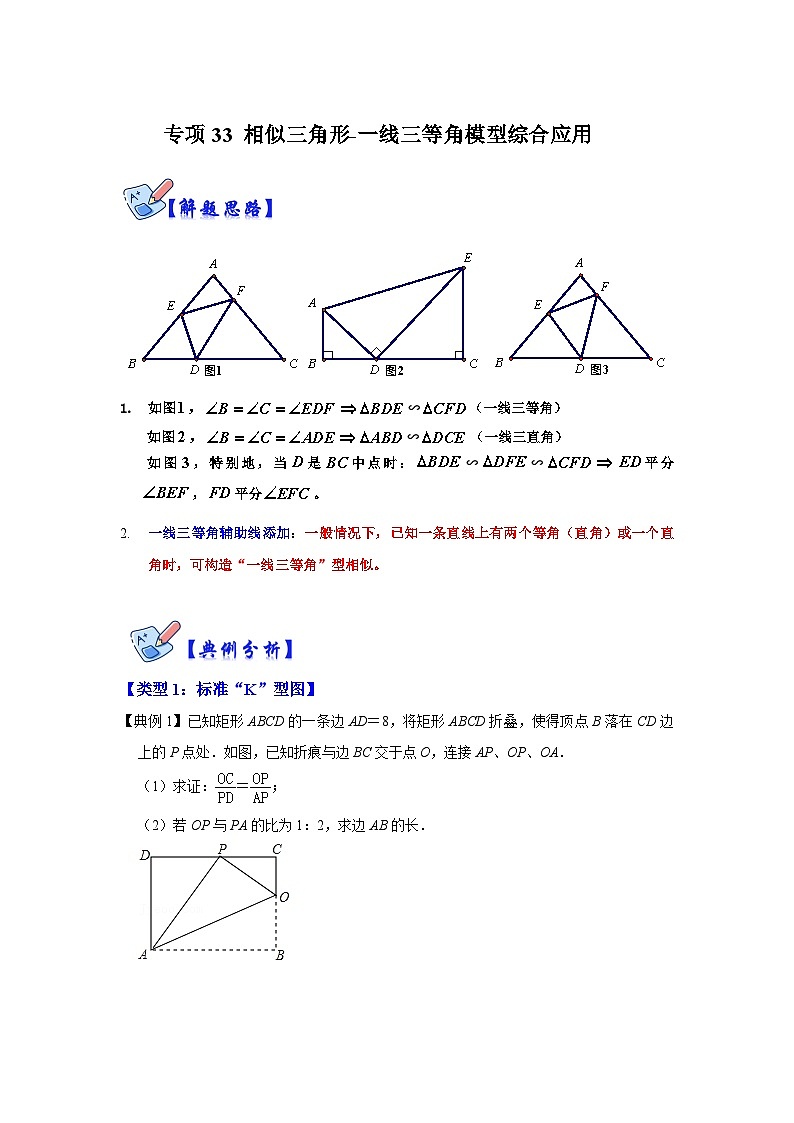
如图，∽（一线三等角）
如图，∽（一线三直角）
如图，特别地，当是中点时：∽∽平分，平分。
一线三等角辅助线添加：一般情况下，已知一条直线上有两个等角（直角）或一个直角时，可构造“一线三等角”型相似。
【类型1：标准“K”型图】
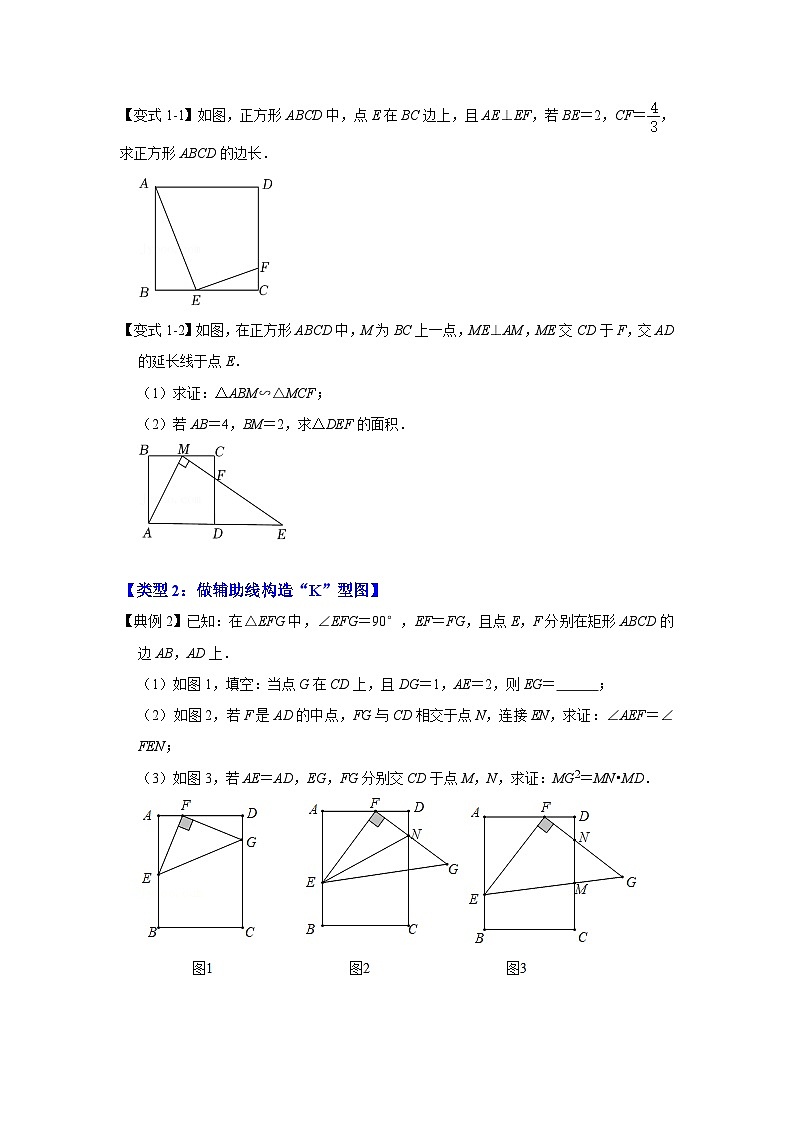
【典例1】已知矩形ABCD的一条边AD＝8，将矩形ABCD折叠，使得顶点B落在CD边上的P点处．如图，已知折痕与边BC交于点O，连接AP、OP、OA．
（1）求证：＝；
（2）若OP与PA的比为1：2，求边AB的长．
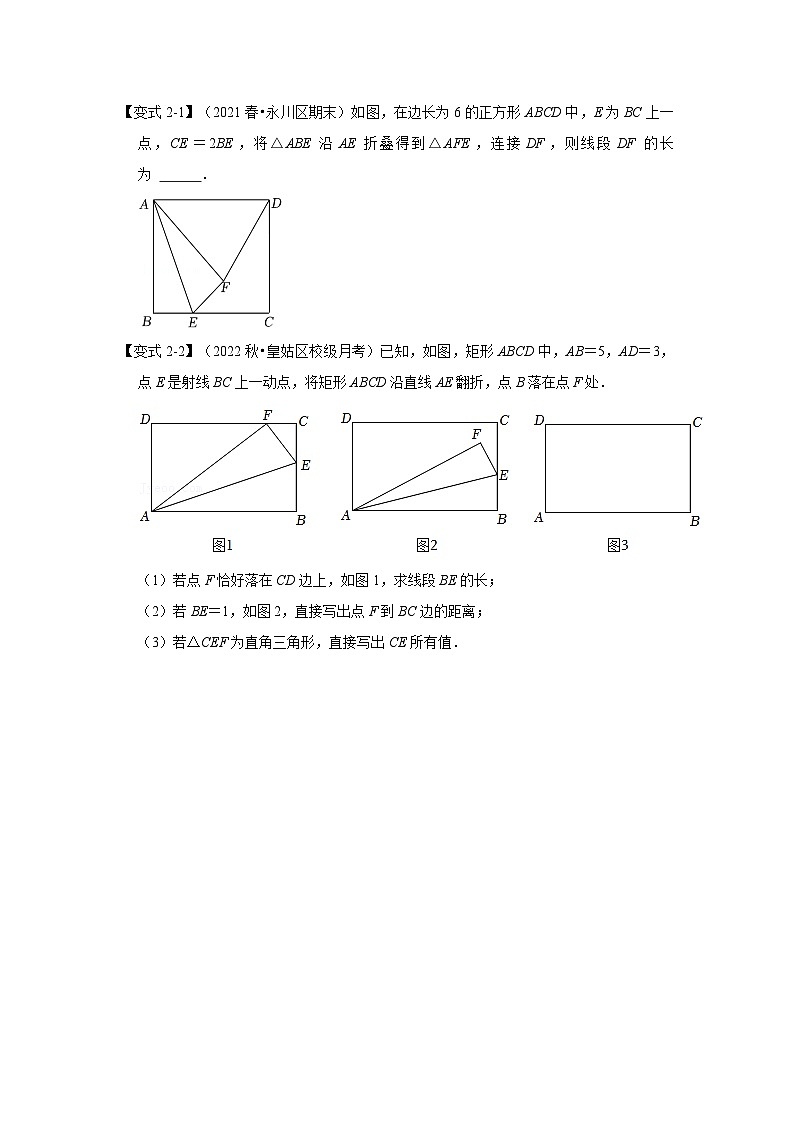
【变式1-1】如图，正方形ABCD中，点E在BC边上，且AE⊥EF，若BE＝2，CF＝，求正方形ABCD的边长．
【变式1-2】如图，在正方形ABCD中，M为BC上一点，ME⊥AM，ME交CD于F，交AD的延长线于点E．
（1）求证：△ABM∽△MCF；
（2）若AB＝4，BM＝2，求△DEF的面积．
【类型2：做辅助线构造“K”型图】
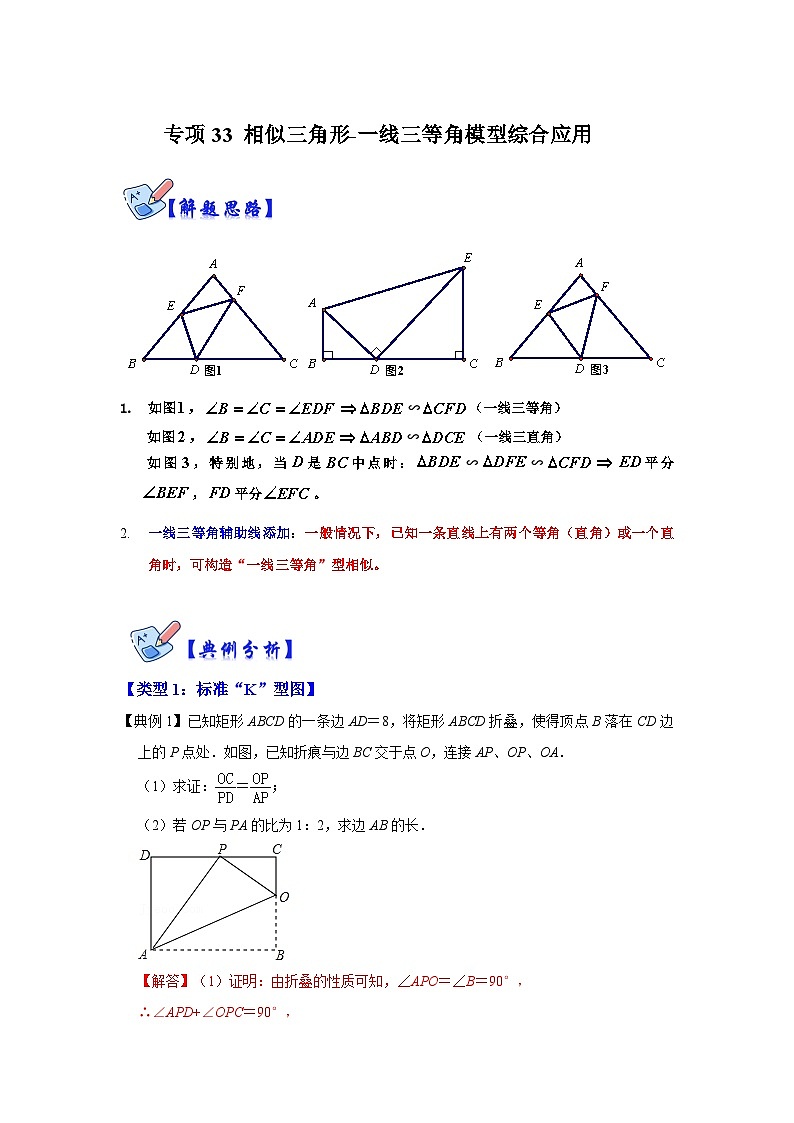
【典例2】已知：在△EFG中，∠EFG＝90°，EF＝FG，且点E，F分别在矩形ABCD的边AB，AD上．
（1）如图1，填空：当点G在CD上，且DG＝1，AE＝2，则EG＝ ；
（2）如图2，若F是AD的中点，FG与CD相交于点N，连接EN，求证：∠AEF＝∠FEN；
（3）如图3，若AE＝AD，EG，FG分别交CD于点M，N，求证：MG2＝MN•MD．
【变式2-1】（2021春•永川区期末）如图，在边长为6的正方形ABCD中，E为BC上一点，CE＝2BE，将△ABE沿AE折叠得到△AFE，连接DF，则线段DF的长为 ．
【变式2-2】（2022秋•皇姑区校级月考）已知，如图，矩形ABCD中，AB＝5，AD＝3，点E是射线BC上一动点，将矩形ABCD沿直线AE翻折，点B落在点F处．
（1）若点F恰好落在CD边上，如图1，求线段BE的长；
（2）若BE＝1，如图2，直接写出点F到BC边的距离；
（3）若△CEF为直角三角形，直接写出CE所有值．
【类型2：特殊“K”型图】
【典例3】（2021秋•通许县期中）感知：
（1）数学课上，老师给出了一个模型：如图1，∠BAD＝∠ACB＝∠AED＝90°，由∠1+∠2+∠BAD＝180°，∠2+∠D+∠AED＝180°，可得∠1＝∠D；又因为∠ACB＝∠AED＝90°，可得△ABC∽△DAE，进而得到＝ ．我们把这个数学模型称为“一线三等角”模型．
应用：
（2）实战组受此模型的启发，将三等角变为非直角，如图2，在△ABC中，点D在边BC上，并且DA＝DE，∠B＝∠ADE＝∠C．若BC＝a，AB＝b，求CE的长度（用含a，b的代数式表示）．
拓展：
（3）创新组突发奇想，将此模型迁移到平行四边形中，如图3，在▱ABCD中，E为边BC上的一点，F为边AB上的一点．若∠DEF＝∠B．求证：AB•FE＝BE•DE．
【变式3-1】如图，AB＝9，AC＝8，P为AB上一点，∠A＝∠CPD＝∠B，连接CD．
（1）若AP＝3，求BD的长；
（2）若CP平分∠ACD，求证：PD2＝CD•BD．
【变式3-2】（2022春•定海区校级月考）【基础巩固】
（1）如图1，在△ABC中，∠ACB＝90°，直线l过点C，分别过A、B两点作AE⊥l，BD⊥l，垂足分别为E、D．求证：△BDC∽△CEA．
【尝试应用】
（2）如图2，在△ABC中，∠ACB＝90°，D是BC上一点，过D作AD的垂线交AB于点E．若BE＝DE，，AC＝20，求BD的长．
【拓展提高】
（3）如图3，在平行四边形ABCD中，在BC上取点E，使得∠AED＝90°，若AE＝AB，，CD＝，求平行四边形ABCD的面积．
1．（2021秋•南京期末）如图，在矩形ABCD中，E，F，G分别在AB，BC，CD上，DE⊥EF，EF⊥FG，BE＝3，BF＝2，FC＝6，则DG的长是（ ）
A．4B．C．D．5
2．（2022秋•二道区月考）如图，在△ABC中，AB＝AC＝9，BC＝12，D，E分别是BC，AB上的动点（点D与B，C不重合），且2∠ADE+∠BAC＝180°，若BE＝4，则CD的长为 ．
3．（2022•杭州模拟）如图，点E是矩形ABCD边BC上一点，沿AE折叠，点B恰好落在CD边上的点F处．设＝x（x＞1），
（1）若点F恰为CD边的中点，则x＝ ．
（2）设＝y，则y关于x的函数表达式是 ．
4．（2021•海州区校级二模）如图，△DEF的三个顶点分别在等边△ABC的三条边上，BC＝4，∠EDF＝90°，＝，则DF长度的最小值是 ．
5.如图，在等边三角形ABC中，点E，D分别在BC，AB上，且∠AED＝60°，求证：△AEC∽△EDB．
6.如图，在等腰直角△ABC中，∠BAC＝90°，AB＝AC，点D、E分别在边BC、AC上，连接AD、DE，有∠ADE＝45°．
（1）证明：△BDA∽△CED．
（2）若BC＝6，当AE＝ED时，求BD的长．
7．（2022•安徽三模）如图，在四边形ABCD中，∠A＝∠D＝90°，AD＝AB，以BC为直径的半⊙O与边AD相切于点E．
（1）求证：∠BCE＝∠DCE；
（2）若，求DE的长．
8．（2022•钦州一模）已知下列各图中，△ABC是直角三角形，∠ABC＝90°．
【基本模型感知】如图1，分别过A，C两点作经过点B的直线的垂线，垂足分别为M、N．求证：△ABM∽△BCN；
【基本模型应用】如图2，点P是边BC上一点，∠BAP＝∠C，，求tanC的值；
【灵活运用】如图3，点D是边CA延长线上一点，AE＝AB，∠DEB＝90°，，，请直接写出tan∠BEC的值．
9．（2021•坪山区一模）如图，抛物线y＝x2+bx+c与x轴交于点A（﹣3，0）、B，与y轴交于点C（0，﹣3）．
（1）求抛物线的解析式；
（2）在抛物线上求点P，使S△BCP＝2S△BCO，求点P的坐标；
（3）如图2，直线y＝x+3交抛物线于第一象限的点M，若N是抛物线y＝x2+bx+c上一点，且∠MAN＝∠OCB，求点N的坐标．