高三数学【大题规范训练】30套（教师版+学生版）

这是一份高三数学【大题规范训练】30套（教师版+学生版），文件包含高三数学大题规范训练7教师版docx、高三数学大题规范训练10原卷版docx、高三数学大题规范训练4原卷版docx、高三数学大题规范训练1原卷版docx、高三数学大题规范训练16原卷版docx、高三数学大题规范训练20原卷版docx、高三数学大题规范训练3原卷版docx、高三数学大题规范训练2原卷版docx、高三数学大题规范训练5原卷版docx、高三数学大题规范训练6原卷版docx、高三数学大题规范训练30原卷版docx、高三数学大题规范训练7原卷版docx、高三数学大题规范训练8原卷版docx、高三数学大题规范训练29原卷版docx、高三数学大题规范训练28原卷版docx、高三数学大题规范训练27原卷版docx、高三数学大题规范训练26原卷版docx、高三数学大题规范训练25原卷版docx、高三数学大题规范训练23原卷版docx、高三数学大题规范训练22原卷版docx、高三数学大题规范训练9原卷版docx、高三数学大题规范训练21原卷版docx、高三数学大题规范训练24原卷版docx、高三数学大题规范训练12原卷版docx、高三数学大题规范训练11原卷版docx、高三数学大题规范训练13原卷版docx、高三数学大题规范训练14原卷版docx、高三数学大题规范训练19原卷版docx、高三数学大题规范训练15原卷版docx、高三数学大题规范训练17原卷版docx、高三数学大题规范训练18原卷版docx、高三数学大题规范训练14解析版docx、高三数学大题规范训练17解析版docx、高三数学大题规范训练12解析版docx、高三数学大题规范训练15解析版docx、高三数学大题规范训练20解析版docx、高三数学大题规范训练10解析版docx、高三数学大题规范训练18解析版docx、高三数学大题规范训练6解析版docx、高三数学大题规范训练8解析版docx、高三数学大题规范训练27解析版docx、高三数学大题规范训练25解析版docx、高三数学大题规范训练13解析版docx、高三数学大题规范训练21解析版docx、高三数学大题规范训练24解析版docx、高三数学大题规范训练2解析版docx、高三数学大题规范训练30解析版docx、高三数学大题规范训练3解析版docx、高三数学大题规范训练5解析版docx、高三数学大题规范训练19解析版docx、高三数学大题规范训练23解析版docx、高三数学大题规范训练4解析版docx、高三数学大题规范训练22解析版docx、高三数学大题规范训练16解析版docx、高三数学大题规范训练11解析版docx、高三数学大题规范训练28解析版docx、高三数学大题规范训练29解析版docx、高三数学大题规范训练9解析版docx、高三数学大题规范训练26解析版docx、高三数学大题规范训练1解析版docx等60份试卷配套教学资源，其中试卷共375页， 欢迎下载使用。

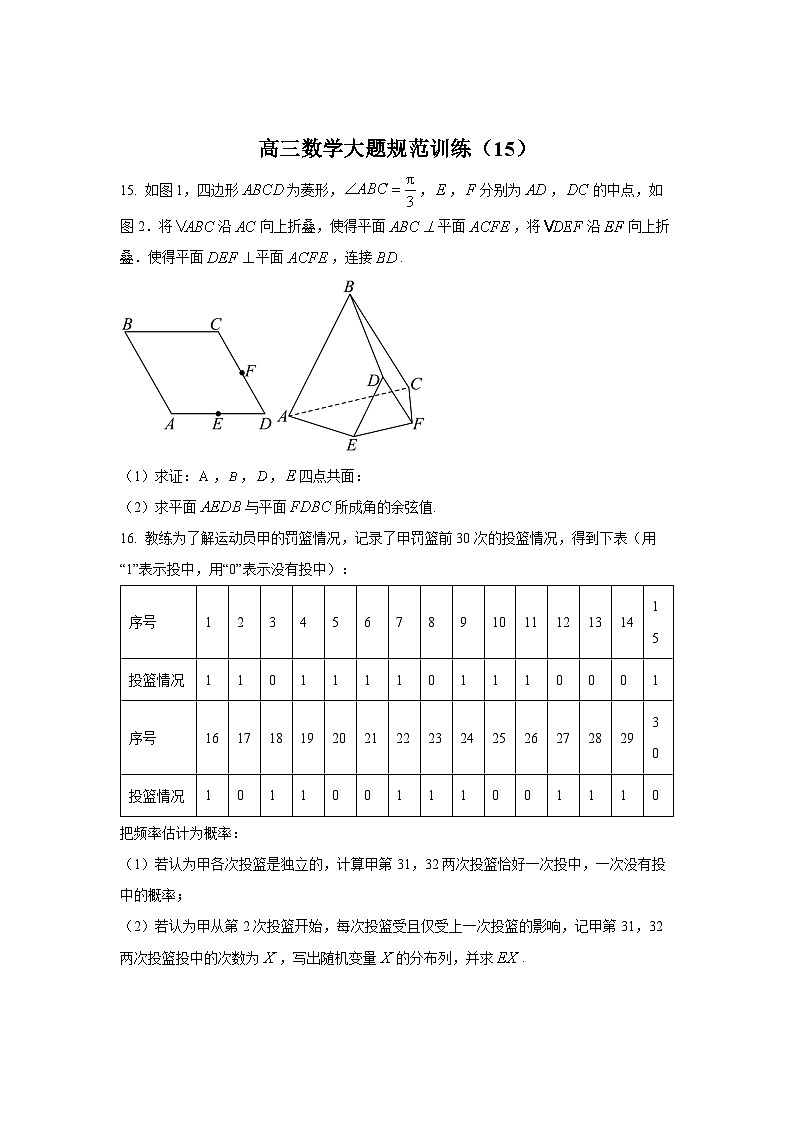
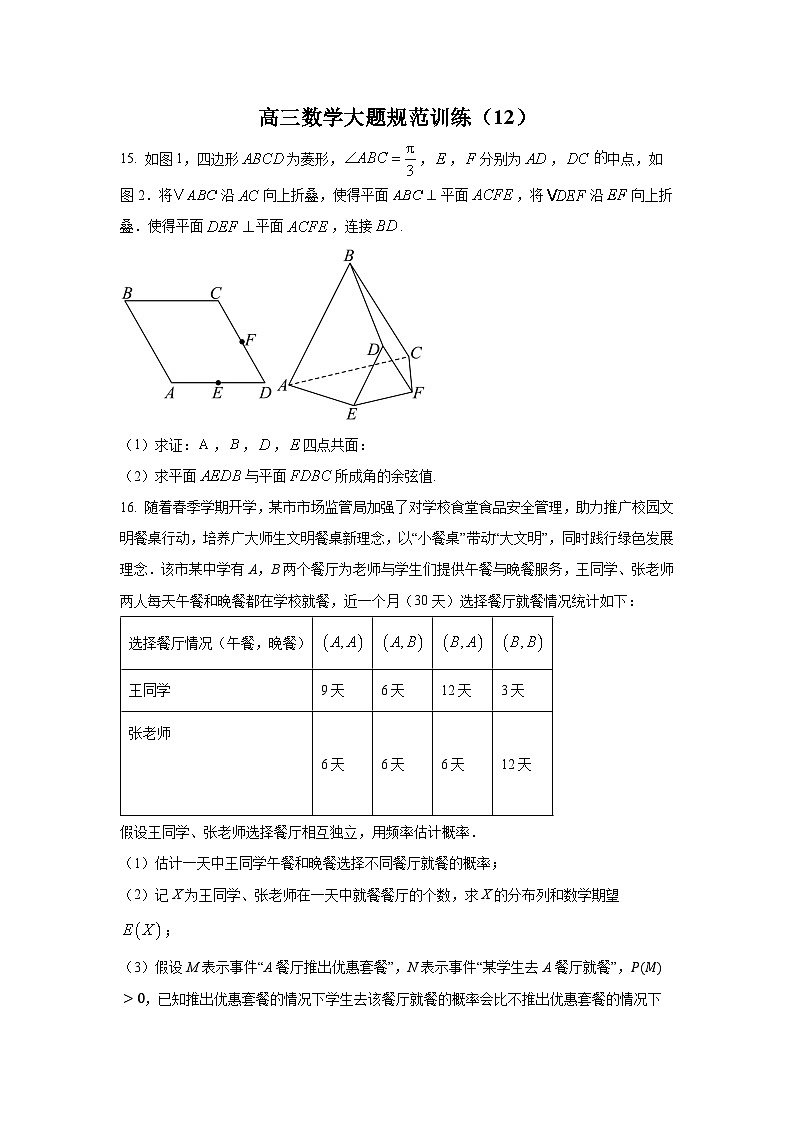
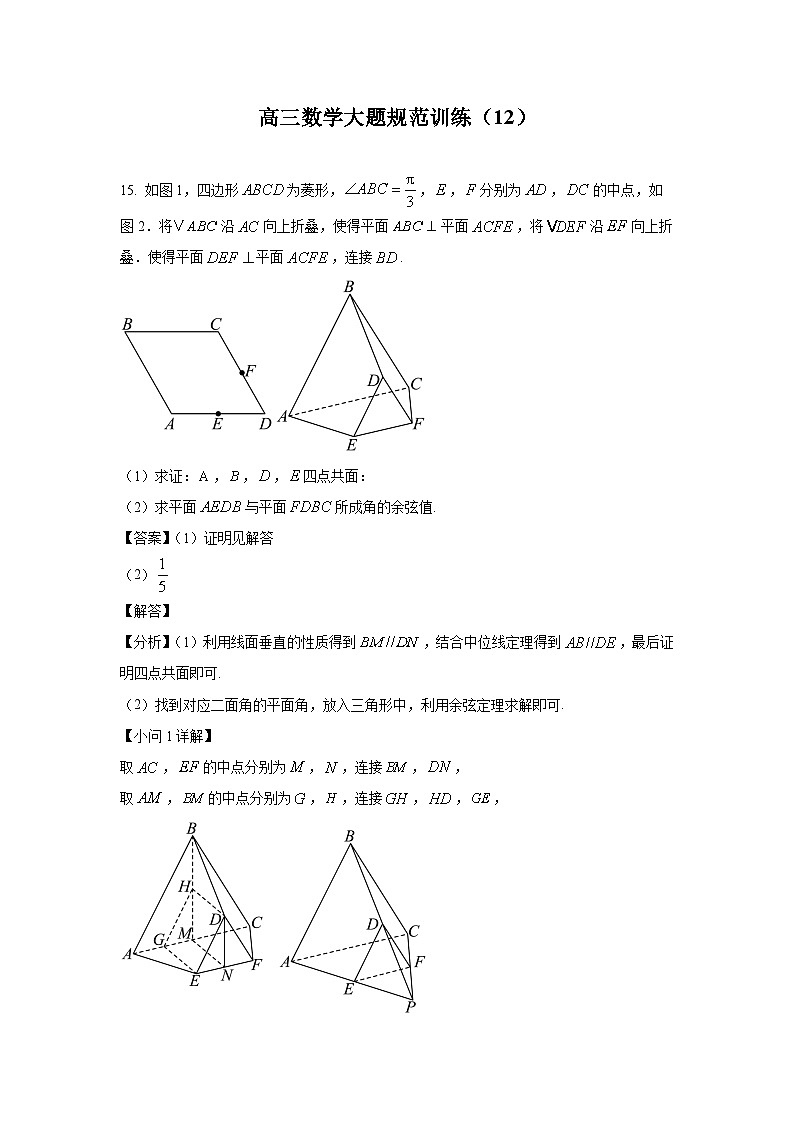
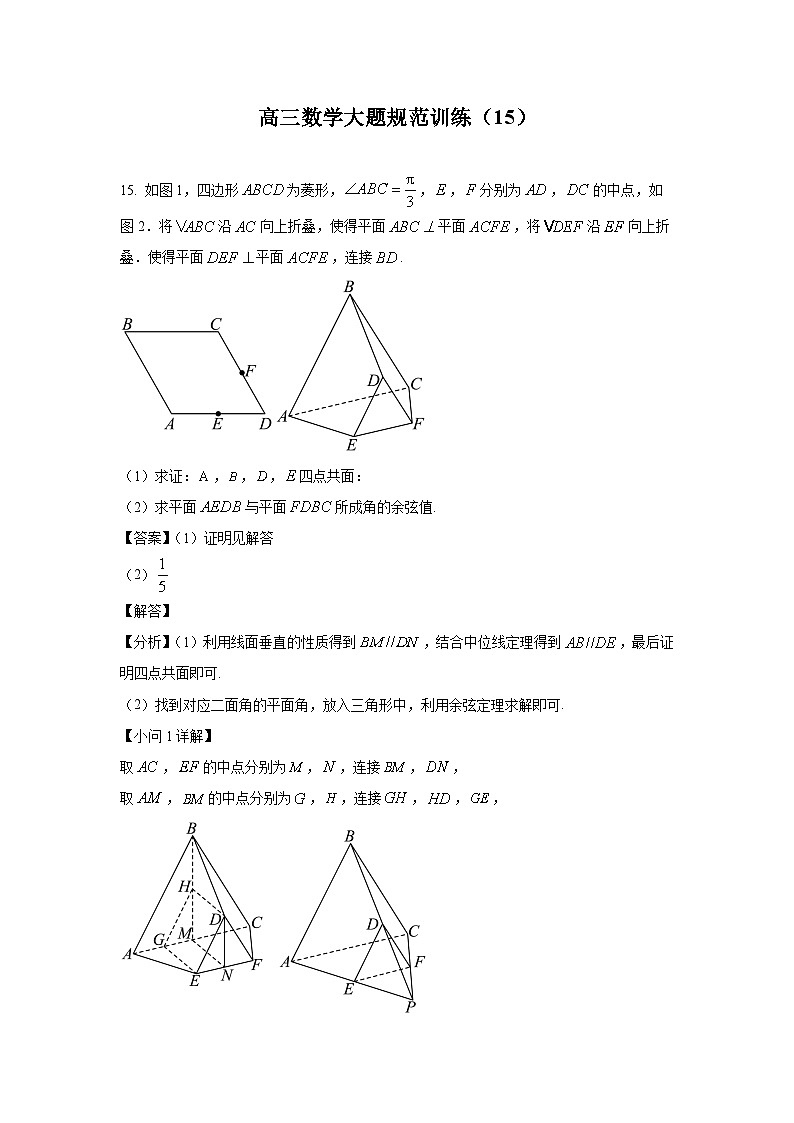
15. ，，分别为的内角，，的对边.已知.
（1）求；
（2）若，，求的周长.
【答案】（1）
（2）
【解答】
【分析】（1）利用正弦定理化简已知条件，求得，进而求得.
（2）利用余弦定理求得，进而求得的周长.
【小问1详解】
因为，
所以由正弦定理得，
即，又，所以，
所以为锐角，所以，
故 ；
【小问2详解】
因为，，
所以，
整理得，解得（负根舍去），
所以，，
所以的周长为.
16. 某视力研究中心为了解大学生的视力情况，从某大学抽取了60名学生进行视力测试，其中男生与女生的比例为，男生近视的人数占总人数的，男生与女生总近视人数占总人数的.
（1）完成下面列联表，并依据小概率值的独立性检验，能否认为是否近视与性别有关.
（2）按性别用分层抽样的方法从近视的学生中抽取8人，若从这8人中随机选出2人进行平时用眼情况调查，求选出的2人中女生人数的分布列和数学期望.
附：.
【答案】（1）表格见解答，无关
（2）分布列见解答，.
【解答】
【分析】（1）根据已知中的数据信息可以补全二阶列联表，并利用卡方公式进行计算，根据小概率值的独立性检验，把卡方值与6.635比较，从而作出判断.
（2）利用分层抽样确定样本中8人，男生有6人，女生有2人，再从中抽取2人，这就是超几何分布，由此可计算出结果.
【小问1详解】
由题意，男生与女生的人数之比是，所以男生有人，女生有人，男生近视的人数占总人数的，所以有人，男生中不近视的人数为15人，
男生与女生总的近视人数占总人数的，所以总的近视人数为，则女生中近视的人数为人.
可得如下列联表：
零假设为：性别与近视情况独立，即性别因素与学生近视情况无关；
所以，
根据小概率值的独立性检验，没有充分证据推断不成立，因此可以认为成立，即性别因素与学生近视情况无关.
【小问2详解】
男生与女生总的近视的学生一共有40人，其中男生近视人数是25人，女生近视人数是15人，从中抽取8人，抽到的男生人数､女生人数分别为：.
所以从这8人中随机抽取2人，其中女生人数的所有可能取值为.
，
所以的分布列为
即.
17. 如图，在四棱锥中，底面为平行四边形，侧面是边长为2的正三角形，平面平面，．
（1）求证：平面；
（2）若E为侧棱的中点，且点到平面的距离为，求平面与平面夹角的余弦值．
【答案】（1）证明见解答
（2）
【解答】
【分析】（1）设Q为AD的中点，连接PQ，证明平面ABCD，得， 从而可证线面垂直；
（2）建立如图所示的空间直角坐标系，用空间向量法求二面角．
【小问1详解】
设Q为AD的中点，连接PQ，
∵正三角形，∴，
又平面平面ABCD，平面平面，平面PAD ，
∴平面ABCD，
又平面ABCD，∴，
又，，平面PAD ，∴平面PAD；
【小问2详解】
在平面PAD内作，则．
∵平面PAD，平面PAD，平面PAD，∴，．
如图所示，以A为坐标原点，AB，AD，AM所在直线分别为x轴、y轴、z轴，
建立空间直角坐标系．
∵底面ABCD为平行四边形，，∴ABCD为矩形．
设，则，，，，，．
∴，
设平面ACE的法向量为，
由得
取，得平面ACE的一个法向量为．
又，所以点B到平面ACE的距离为，
解得．
∴，，，
设平面ABP的法向量为，
由得
取，得平面ABP的一个法向量为．
∴平面ACE与平面ABP夹角的余弦值为 ．
18. 已知椭圆的左，右焦点分别为，椭圆E的离心率为，椭圆E上的点到右焦点的最小距离为1．
（1）求椭圆E的方程；
（2）若过右焦点的直线l与椭圆E交于B，C两点，E的右顶点记为A，，求直线l的方程．
【答案】（1）
（2）或
【解答】
【分析】（1）利用椭圆焦半径公式及性质计算即可；
（2）设直线l方程，B、C坐标，根据平行关系得出两点纵坐标关系，联立椭圆方程结合韦达定理解方程即可.
【小问1详解】
设焦距为，由椭圆对称性不妨设椭圆上一点，
易知，则
，
显然时，
由题意得解得，
所以椭圆的方程为；
【小问2详解】
设，
因为，所以
所以①
设直线的方程为，联立得，整理得，
由韦达定理得，
把①式代入上式得，得，
解得，
所以直线的方程为：或.

19. 已知函数．
（1）求的极值；
（2）若在区间有2个零点，求的取值范围．
【答案】（1）当时，在处取极大值
（2）
【解答】
【分析】（1）根据题意，求导得，然后分与讨论，即可得到结果；
（2）根据题意，将问题转化为与在区间有2个交点，求得函数的值域，即可得到结果.
【小问1详解】
因为，定义域为，所以，
当时，由于，则恒成立，
所以在上单调递增，无极值，
当时，令，解得，
当时，，则在上单调递增；
当时，，则在上单调递减：
所以当时，在处取极大值，无极小值；
【小问2详解】
，
令，得，令，在区间有2个零点，
即与在区间有2个交点，
，，，
当，，在上单增，
当，，在上单减，
，的最大值为，，
与在区间有2个交点，则．近视
不近视
合计
男
女
合计
60
0.100
0.050
0.025
0010
0001
2.706
3.841
5.024
6.635
10.828
近视
不近视
合计
男
25
15
40
女
15
5
20
合计
40
20
60
0
1
2