苏科版（2024）七年级上册（2024）6.1 直线、射线、线段背景图ppt课件

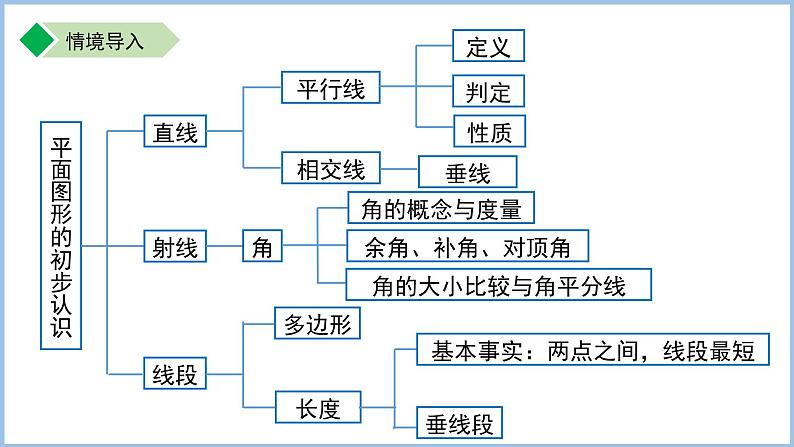
这是一份苏科版（2024）七年级上册（2024）6.1 直线、射线、线段背景图ppt课件，共30页。PPT课件主要包含了平面图形的初步认识，平行线，相交线，角的概念与度量，补角对顶角，多边形，垂线段，知识点一四组概念，AMAN，概念2角等内容，欢迎下载使用。
角的大小比较与角平分线
基本事实：两点之间，线段最短
概念1 直线、射线、线段
直线的特征：①笔直的；②没有端点；③向两方无限延伸；④无法度量，无长短.
射线的特征：①笔直的；②只有一个端点；③向一方无限延伸；④无法度量，无长短.
线段的特征：①笔直的；②有两个端点；③不可延伸；④可以度量，有长短.
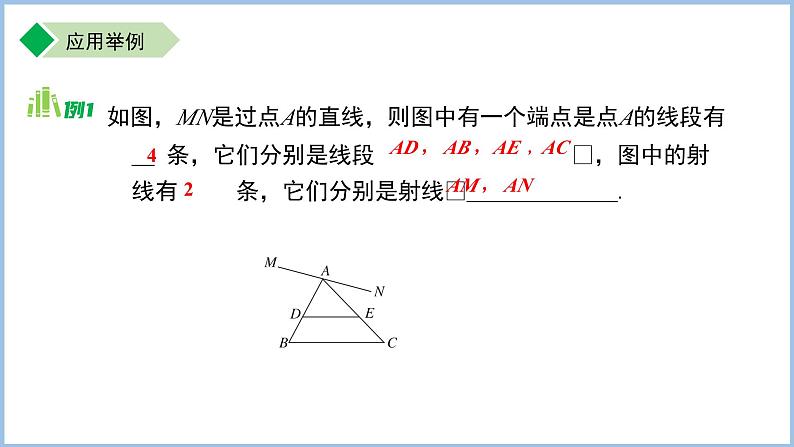
如图，MN是过点A的直线，则图中有一个端点是点A的线段有__ 条，它们分别是线段 ⁠，图中的射线有 条，它们分别是射线⁠______________.
AD ， AB ，AE ，AC
AM ， AN
定义:角是由两条具有公共端点的射线组成的。
表示:① 用三个英文大写字母表示（表示顶点的字母写在中间）
②当以某顶点的角只有一个时，也可以用顶点的大写字母来表示.
③ 用一个数字或者希腊字母表示
如图，能用一个大写字母表示的角有 ,可用三个大写字母表示的角是 ⁠___(任写三个)；以D为顶点的角是__________________
∠ ACD ，∠ DCB ，∠ ACB
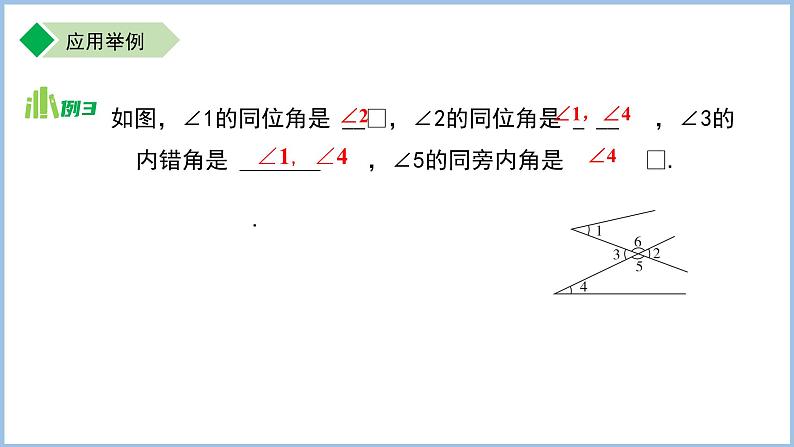
概念3 同位角、内错角、同旁内角
同位角： ∠1和∠2， ∠3和∠4， ∠5和∠6， ∠7和∠8
内错角： ∠7和∠2， ∠5和∠4
同旁内角： ∠7和∠4， ∠5和∠2
如图，∠1的同位角是 __⁠，∠2的同位角是 _ __ ，∠3的内错角是 _______ ，∠5的同旁内角是 ⁠.
概念4 多边形 (1)从六边形的一个顶点出发，可以画m 条对角线，它们将六边形分成 n 个三角形，则 m ＋ n 的值为(　　)
(2)如图，△ CAB 的外角等于120°，∠ B 等于40°，则∠ C 的度数是_________.
(1)尺规作图：已知∠α，∠β，作∠ AOB ，使∠ AOB ＝∠α＋∠β(不用写作法，保留作图痕迹).
解：作图如下，∠ AOB 即为所作.
作图2 垂线的作图
(2)如图所示，火车站、码头分别位于 A ，B 两点，直线a和b分 别表示河流与铁路.
①从火车站到码头怎样走最近?
沿 AB 走最近.理由：两点之间线段最短.
②从码头到铁路怎样走最近?
沿 AC 走最近.理由：直线外一点与直线上各点连接的所有线段中，垂线段最短.
作图3 平行线的作图
(3)如图，P 是∠AOB 外一点.
①过点 P 画 OA 的平行线，交 OB 于点 C.
②过点 P 画 OB 的平行线，交 OA 的反向延长线于点 D
③量出∠ AOB ，∠ PCO ，∠ PDO ，∠ CPD 的度数.你有什么发现？
解：∠ AOB ＝43°，∠ PCO ＝43°，∠ PDO ＝43°，∠ CPD ＝137°发现：如果两个角的两边互相平行，则这两个角相等或互补.
如图，已知线段 AB ＝4，延长 AB 到点 C ，使得 AB ＝2 BC ，反向延长 AB 到点 D ，使 AC ＝2 AD . (1)求线段 CD 的长；
解：(1)因为 AB ＝4， AB ＝2 BC ， 所以 BC ＝2.所以 AC ＝ AB ＋ BC ＝6. 又因为 AC ＝2 AD ，所以 AD ＝3. 所以 CD ＝ AC ＋ AD ＝6＋3＝9.
(1) 34.37°＝ ° ' ″；108°21'36″ ＝_________
(2)钟表在9点30分时，它的时针与分针所夹的角是 ⁠.
(3)已知一个角的补角比这个角的余角的3倍大10°，则这个角的度数是 ⁠.
(4)点 O 是直线 AB 上一点，∠ COD 是直角， OE 平分∠ BOC . ① 如图，若∠ DOE ＝25°，求∠ AOC 的度数；
解：(1)因为∠ COD ＝90°，∠ DOE ＝25°， 所以∠ COE ＝∠ COD －∠ DOE ＝90°－25°＝65°. 又因为 OE 平分∠ BOC ，所以∠ BOC ＝2∠ COE ＝130°. 所以∠ AOC ＝180°－∠ BOC ＝180°－130°＝50°.
(4)点 O 是直线 AB 上一点，∠ COD 是直角， OE 平分∠ BOC .
②将图中的∠ COD 绕点 O 按顺时针方向旋转至图所示位置.探究∠ DOE 与∠ AOC 之间的数量关系，写出你的结论，并说明理由.
知识点四：根据基本事实说理
(1)“把弯曲的公路改直，就能缩短路程”，其中蕴含的数学道理是_________________________.
(2)国庆节前，某绿化公司在公园的入口两边摆放时令花卉，小明观察到工人们先在两端各确定一点，并拉绳固定，再沿绳子规范地摆放中间的花，工人们这样操作，可用学过的知识解释为 ⁠.
知识点五：平行线的判定
判定:①同位角相等，两直线平行.
②内错角相等，两直线平行.
③同旁内角互补，两直线平行.
如图，在三角形 ABC 中，点 D ， F 在边 BC 上，点 E 在边 AB 上，点 G 在边 AC 上， EF 与 GD 的延长线交于点 H ，∠1＝∠ B ，∠2＋∠3＝180°.(1)判断 EH 与 AD 的位置关系，并说明理由；
解：(1) EH ∥ AD . 理由如下：因为∠1＝∠ B ，所以 AB ∥ GD . 所以∠2＝∠ BAD . 因为∠2＋∠3＝180°，所以∠ BAD ＋∠3＝180°.所以 EH ∥ AD .
(2)若∠ DGC ＝58°，且∠ H ＝∠4＋10°，求∠ H 的度数.
解：由(1)得 AB ∥ GD ，所以∠ DGC ＝∠ BAC . 因为∠ DGC ＝58°，所以∠ BAC ＝58°.因为 EH ∥ AD ，所以∠2＝∠ H . 又因为∠2＝∠ BAD ，
所以∠ H ＝∠ BAD . 所以∠ BAC ＝∠ BAD ＋∠4＝∠ H ＋∠4＝58°.又因为∠ H ＝∠4＋10°，所以∠4＋10°＋∠4＝58°，解得∠4＝24°.所以∠ H ＝34°.
知识点六：平行线的性质
性质：①两直线平行，同位角相等.
②两直线平行，内错角相等.
③两直线平行，同旁内角互补.
如图是一个汉字“互”的形状，其中 EG 的延长线与 AB 交于点 M ，HF 的延长线与 CD 交于点 N ， GH ∥ EF ， AB ∥ CD ，∠ EGH ＝∠ EFH . (1)试说明∠ MEF ＝∠ GHN ；
解：(1) 因为 GH ∥ EF ， 所以∠ EGH ＋∠ GEF ＝180°，∠ MGH ＝∠ MEF . 因为∠ EGH ＝∠ EFH ，所以∠ GEF ＋∠ EFH ＝180°. 所以 ME ∥ HN . 所以∠ MGH ＝∠ GHN . 所以∠ MEF ＝∠ GHN .
如图是一个汉字“互”的形状，其中EG 的延长线与 AB 交于点 M ，HF 的延长线与CD交于点N ， GH∥EF ， AB∥CD ，∠EGH ＝∠EFH . (2)若∠1＝70°，求∠2的度数.
解：(2) 如图，延长 ME 交 CD 于点 P . 因为AB∥CD ，所以∠1＝∠MPN . 由(1)知ME∥HN ，所以∠2＝∠MPN . 所以∠1＝∠2.又因为∠1＝70°，所以∠2＝70°.
2.点到直线的距离是（ ）A.点到直线的垂线段的长度B.点到直线的垂线段C.点到直线的垂线D.点到直线上一点的连线
3.如图，已知AC⊥BC,CD⊥AB于点D,AC=3,BC=4,则点B到直线AC的距离等于 ，点A到直线BC的距离等于 ，点C到直线AB的垂线段是线段 .
1.连接两点之间 叫做两点间的距离；
4.如图，正方形网格的边长为1，点P是∠AOB的边OB上的一格点.(1)过点P画OB的垂线，交OA于点C；(2)过点P画OA的垂线，垂直为H；(3)点P到OA的距离为 ；(4)试判断线段PC，PH，OC的大小关系，并说明理由.
OC>PC>PM理由：垂线段最短
5.如图，直线AB，CD相交于点O，OE平分∠BOD.(1)若∠AOC=50°，求∠BOE的度数；(2)若OF平分∠COB，能判断OE⊥OF吗？说明理由.
解：（1）因为∠AOC=50° 所以∠BOD=∠AOC=50°(对顶角相等） 因为OE平分∠BOD 所以∠BOE= ∠BOD=25°
解：(2) 因为OE平分∠BOD，∠BOD=50° 所以∠1=∠2=25°.（角平分线的定义） 因为∠BOD+∠BOC=180°，(平角的定义） 所以∠BOC=130°. 因为OF平分∠BOC， 所以∠3=65°， 所以∠3+∠2=65°+25°=90°， 所以OE⊥OF.