2021-2022学年广东省广州市越秀区铁一中学九年级（上）期末数学试卷（含答案）

这是一份2021-2022学年广东省广州市越秀区铁一中学九年级（上）期末数学试卷（含答案），共33页。试卷主要包含了选择题，解答题等内容，欢迎下载使用。
1．（3 分）下列四个图形中，是中心对称图形的是()
A． B． C． D．
2．（3 分）下面四组线段中，成比例的是()
A． a  1 ， b  2 ， c  2 ， d  4
B． a  2 ， b  3 ， c  4 ， d  5
C． a  4 ， b  6 ， c  8 ， d  10
D． a 
2,b 
3, c  3, d 
3
3．（3 分）下列事件中，随机事件的个数为()
①连续两次抛掷一枚骰子，两次都出现 2 点向上；②13 个人中至少有两个人生肖相同；③ 某人买彩票中奖；④任意买一张电影票，座位号是 2 的倍数．
A．1 个B．2 个C．3 个D．4 个
4．（3 分）已知O 的半径为 6， A 为线段 PO 的中点，当OP  12 时，点 A 与O 的位置关系为()
A．点 A 在O 上B．点 A 在O 外
C．点 A 在O 内D．点 A 与O 位置不确定
5．（3 分）如图，O 的直径CD 垂直弦 AB 于点 E ，且CE  4 ，OB  8 ，则 AB 的长为()
3
3
A． 4B．4C．6D． 8
6．（3 分）若 A(4, y ) ，B(3, y ) ，C(1, y ) 为二次函数 y  x2  4x 1的图象上的三点，则 y ，
1231
y2 ， y3 的大小关系是()
y1  y2  y3
y2  y1  y3
y3  y1  y2
y1  y3  y2
7．（3 分）根据下列表格对应值：
判断关于 x 的方程 ax2  bx  c  0(a  0) 的一个解 x 的范围是()
x
2.1
2.2
2.3
2.4
2.5
ax2  bx  c
0.12
0.03
0.01
0.06
0.18
A． 2.1  x  2.2
B． 2.2  x  2.3
C． 2.3  x  2.4
D． 2.4  x  2.5
8．（3 分）如图，正比例函数 y  k x 与反比例函数 y  k2 的图象相交于 A 、 B 两点，其中
112x
点 A 的横坐标为 1．当 y1  y2 时， x 的取值范围是()
A． x  1 或 x  1
C． 1  x  0 或0  x  1
B． 1  x  0 或 x  1
D． x  1 或0  x  1
9．（3 分）如图，在钝角三角形 ABC 中， AB  6cm ， AC  12cm ，动点 D 从点 A 出发沿 AB以1cm / s 的速度向点 B 运动，同时动点 E 从点 C 出发沿CA 以 2cm / s 的速度向点 A 运动， 当以 A ， D ， E 为顶点的三角形与ABC 相似时，运动时间是( )
A． 3s 或 4.8sB． 3sC． 4.5sD． 4.5s 或 4.8s
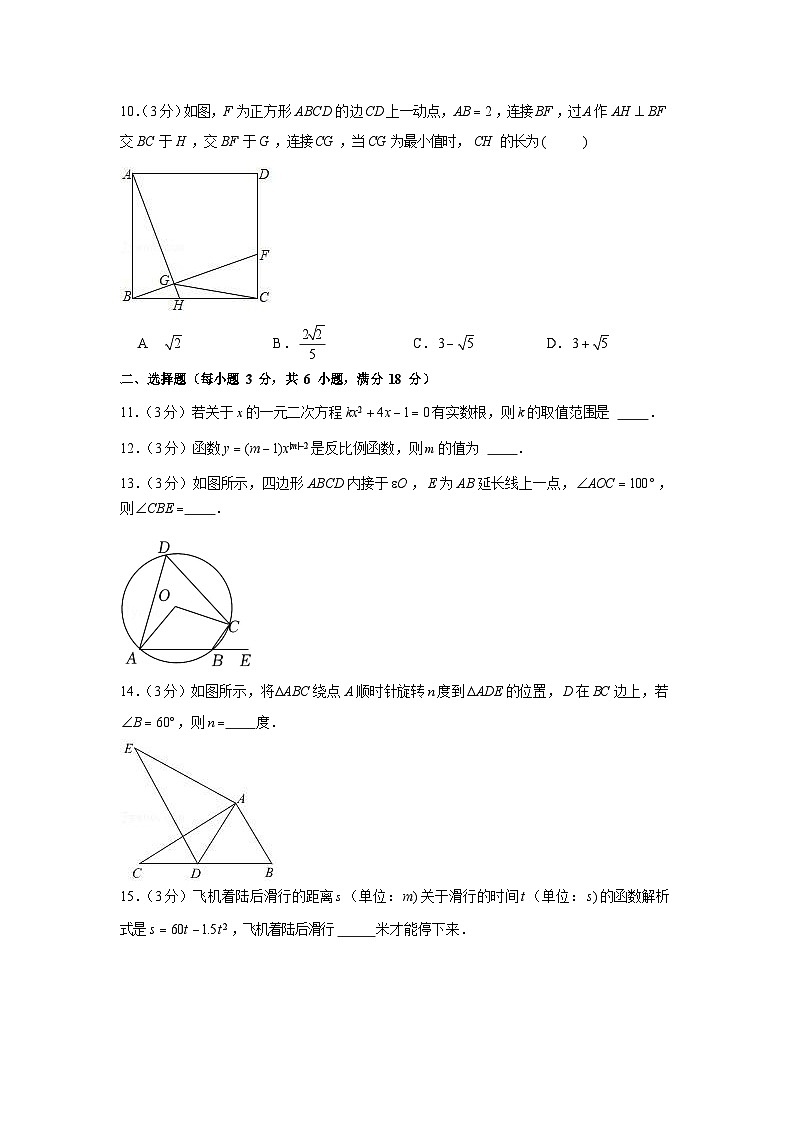
10．（3 分）如图，F 为正方形 ABCD 的边CD 上一动点，AB  2 ，连接 BF ，过 A 作 AH  BF
交 BC 于 H ，交 BF 于G ，连接CG ，当CG 为最小值时， CH 的长为()
2
2 2
5
B．
C． 3 D． 3 
5
5
二、选择题（每小题 3 分，共 6 小题，满分 18 分）
11．（3 分）若关于 x 的一元二次方程 kx2  4x  1  0 有实数根，则 k 的取值范围是 ．
12．（3 分）函数 y  (m 1)x|m|2 是反比例函数，则 m 的值为 ．
13．（3 分）如图所示，四边形 ABCD 内接于O ， E 为 AB 延长线上一点， AOC  100 ，则CBE ．
14．（3 分）如图所示，将ABC 绕点 A 顺时针旋转 n 度到ADE 的位置， D 在 BC 边上，若
B  60 ，则 n 度．
15．（3 分）飞机着陆后滑行的距离 s （单位： m) 关于滑行的时间t （单位： s) 的函数解析式是 s  60t  1.5t 2 ，飞机着陆后滑行米才能停下来．
16．（3 分）抛物线 y  ax2  bx  c 的对称轴是直线 x  1 ，且过点(1, 0) ．顶点位于第二象限，其部分图象如图所示，给出以下判断：① ab  0 且c  0 ；② 4a  2b  c  0 ；③ 8a  c  0 ；
④ c  3a  3b ；⑤直线 y  2x  2 与抛物线 y  ax2  bx  c 两个交点的横坐标分别为 x ， x ，
12
则 x1  x2  x1 x2  5 ．其中结论正确的是．
三、解答题（本大题共 9 小题，满分 102 分，解答应写出文字说明、证明过程或演算步骤）
17．（8 分）解方程： x2  2x ．
18．（8 分）如图，点C 、D 在线段 AB 上，PCD 是等边三角形，且ACP∽PDB ，求APB
的度数．
19．（10 分）如图，点O ， B 的坐标分别是(0, 0) ， (3, 0) ．将OAB 绕点O 逆时针旋转90 ，得到△ OA1B1 ．
画出平面直角坐标系和三角形△ OA1B1 ；
求旋转过程中点 B 走过的路径的长．
20．（10 分）二次函数图象上部分点的横坐标 x ，纵坐标 y 的对应值如表：
求这个二次函数的表达式；
在图中画出这个二次函数的图象；
当函数值 y  0 时，对应的 x 的取值范围是．
x

4
3
2
1
0
1
2

y

5
0
3
4
3
0
5

步数
频数
频率
0x  4000
8
0.16
4000x  8000
15
0.3
8000x  12000
12
a
12000x  16000
b
0.2
16000x  20000
3
0.06
20000x  24000
2
0.04
21．（12 分）随着“微信运动”被越来越多的人关注和喜爱，某数学兴趣小组随机调查了我区 50 名教师某日“微信运动”中的步数情况进行统计整理，绘制了如下的统计图表（不完整）:
请根据以上信息，解答下列问题：
写出 a ， b 的值并补全频数分布直方图；
我市约有 5000 名教师，用调查的样本数据估计日行走步数超过 12000 步（包含 12000
步）的教师有多少名？
若在 50 名被调查的教师中，选取日行走步数超过 16000 步（包含 16000 步）的两名教
师与大家分享心得，用树形图或列表法求被选取的两名教师恰好都在 20000 步（包含 20000
步）以上的概率．
22．（12 分）疫情肆虐，万众一心．由于医疗物资极度匮乏，许多工厂都积极宣布生产医疗物资以应对疫情．某工厂及时引进了 1 条口罩生产线生产口罩，开工第一天生产 300 万个，
第三天生产 432 万个，若每天生产口罩的个数增长的百分率相同，请解答下列问题：
每天增长的百分率是多少？
经调查发现，一条生产线最大产能是 900 万个/ 天，如果每增加 1 条生产线，每条生产线的最大产能将减少 30 万个/ 天．现该厂要保证每天生产口罩 3900 万个，在增加产能同时又要节省投入的条件下（生产线越多，投入越大），应该增加几条生产线？
23．（12 分）如图，一次函数 y  x  b 与反比例函数 y   k (x  0) 的图象交于点 A(m, 4) 和
x
B(4,1) ．
求b 、 k 、 m 的值；
根据图象直接写出x  b   k (x  0) 的解集；
x
点 P 是线段 AB 上一点，过点 P 作 PD  x 轴于点 D ，连接OP ，若POD 的面积为 S ，求 S 的最大值和最小值．
24．（15 分）如图，四边形 ABCD 内接于O ，AC 为直径，AC 和 BD 交于点 E ，AB  BC ．
求ADB 的度数；
过 B 作 AD 的平行线，交 AC 于 F ，试判断线段 EA ， CF ， EF 之间满足的等量关系， 并说明理由；
在（2）条件下过 E ， F 分别作 AB ， BC 的垂线，垂足分别为G ， H ，连接GH ，交
BO 于 M ，若 AG  3 ， S四边形AGMO : S四边形CHMO  8 : 9 ，求O 的半径．
25．（15 分）已知抛物线 y  ax2  bx  c(a  0) 与 x 轴交于 A(1, 0) 、 B 两点，与 y 轴交于点
C(0, 3a) ．
求点 B 的坐标；
若 a  1 ， 点 M 和点 N 在抛物线上，且 M 的横坐标为 4， 点 N 在第二象限，若
2
AMN  2OAM ，求点 N 的坐标；
（3）P 是第四象限内抛物线上的一个动点，直线 PA 、PB 分别交 y 轴于点 M 、N ，判断CM 与CN 的数量关系，并说明理由．
2021-2022 学年广东省广州市越秀区铁一中学九年级（上）期末数学试卷
参考答案与试题解析
一、选择题（每小题 3 分，共 10 小题，满分 30 分）
1．（3 分）下列四个图形中，是中心对称图形的是()
A． B．
C． D．
【分析】根据中心对称图形的概念对各图形分析判断即可得解．
【解答】解： A 、该图形不是中心对称图形，故本选项不合题意；
B 、该图形不是中心对称图形，故本选项不合题意； C 、该图形是中心对称图形，故本选项符合题意； D 、该图形不是中心对称图形，故本选项不合题意； 故选： C ．
【点评】本题考查了中心对称图形的概念，中心对称图形是要寻找对称中心，旋转 180 度后与原图形重合．
2．（3 分）下面四组线段中，成比例的是()
A． a  1 ， b  2 ， c  2 ， d  4
B． a  2 ， b  3 ， c  4 ， d  5
C． a  4 ， b  6 ， c  8 ， d  10
D． a 
2,b 
3, c  3, d 
3
【分析】如果其中两条线段的乘积等于另外两条线段的乘积，则四条线段叫成比例线段．对 选项一一分析，排除错误答案．
【解答】解： A 、1 4  2  2 ，故选项符合题意；
B 、 2  5  3  4 ，故选项不符合题意；
C 、 4 10  6  8 ，故选项不符合题意；
3
C 、 2  3  3 ，故选项不符合题意；
故选： A ．
【点评】此题考查了比例线段，根据成比例线段的概念，注意在相乘的时候，最小的和最大 的相乘，另外两个相乘，看它们的积是否相等．同时注意单位要统一．
3．（3 分）下列事件中，随机事件的个数为()
①连续两次抛掷一枚骰子，两次都出现 2 点向上；②13 个人中至少有两个人生肖相同；③ 某人买彩票中奖；④任意买一张电影票，座位号是 2 的倍数．
个B．2 个C．3 个D．4 个
【分析】事先能肯定它一定会发生的事件称为必然事件，事先能肯定它一定不会发生的事件 称为不可能事件，必然事件和不可能事件都是确定的．
【解答】解：①连续两次抛掷一枚骰子，两次都出现 2 点向上，是随机事件；
②13 个人中至少有两个人生肖相同，是必然事件；
③某人买彩票中奖，是随机事件；
④任意买一张电影票，座位号是 2 的倍数，是随机事件． 故选： C ．
【点评】本题主要考查了随机事件，在一定条件下，可能发生也可能不发生的事件，称为随 机事件．
4．（3 分）已知O 的半径为 6， A 为线段 PO 的中点，当OP  12 时，点 A 与O 的位置关
系为()
A．点 A 在O 上B．点 A 在O 外
C．点 A 在O 内D．点 A 与O 位置不确定
【分析】利用OP  12 ， A 为线段 PO 的中点，则OA  6 ，因而点 A 在O 上．
【解答】解： A 为线段 PO 的中点， OP  12 ，
OA  1 OP  6 ，
2
OA 与圆的半径相等，
点 A 在O 上． 故选： A ．
【点评】本题考查了对点与圆的位置关系的判断．设点到圆心的距离为 d ，则当 d  R 时， 点在圆上；当 d  R 时，点在圆外；当 d  R 时，点在圆内．
5．（3 分）如图，O 的直径CD 垂直弦 AB 于点 E ，且CE  4 ，OB  8 ，则 AB 的长为()
3
3
A． 4B．4C．6D． 8
【分析】根据勾股定理求出 BE ，再根据垂径定理解答即可．
【解答】解：OC  OB  8 ， CE  4 ，
82  42
3
OE  OC  CE  8  4  4 ，
OB2  OE2
在RtOBE 中， BE 
CD  AB ，
 4，
3
 AB  2BE  8，
故选： D ．
【点评】本题考查的是垂径定理、勾股定理，掌握垂直于弦的直径平分这条弦是解题的关键．
6．（3 分）若 A(4, y ) ，B(3, y ) ，C(1, y ) 为二次函数 y  x2  4x 1的图象上的三点，则 y ，
1231
y2 ， y3 的大小关系是()
y1  y2  y3
y2  y1  y3
y3  y1  y2
y1  y3  y2
【分析】分别计算出自变量为4 ， 3 和 1 所对应的函数值，然后比较函数值的大小即可．
【解答】解：当 x  4 时， y1  x  4x 1  16 16 1  1；
2
2
当 x  3 时， y  x2  4x 1  9 12 1  4 ；
当 x  1 时， y3  x  4x 1  1  4 1  4 ；
2
 y2  y1  y3 ， 故选： B ．
【点评】本题考查了二次函数图象上点的坐标特征：二次函数图象上点的坐标满足其解析式．
7．（3 分）根据下列表格对应值：
x
2.1
2.2
2.3
2.4
2.5
判断关于 x 的方程 ax2  bx  c  0(a  0) 的一个解 x 的范围是()
ax2  bx  c
0.12
0.03
0.01
0.06
0.18
A． 2.1  x  2.2
B． 2.2  x  2.3
C． 2.3  x  2.4
D． 2.4  x  2.5
【分析】从表格中的数据可以看出，当 x  2.3 时， y  0.01 ；当 x  2.4 时， y  0.06 ，函
数值由负数变为正数，此过程中存在方程 ax2  bx  c  0 的一个根．
【解答】解：当 x  2.3 时， y  0.01 ；当 x  2.4 时， y  0.06 ，
关于 x 的方程 ax2  bx  c  0(a  0) 的一个解 x 的范围是 2.3  x  2.4 ， 故选： C ．
【点评】本题考查了估算一元二次方程的近似值，对题目的正确估算是建立在对二次函数图 象和一元二次方程关系正确理解的基础上的．
8．（3 分）如图，正比例函数 y  k x 与反比例函数 y  k2 的图象相交于 A 、 B 两点，其中
112x
点 A 的横坐标为 1．当 y1  y2 时， x 的取值范围是()
A． x  1 或 x  1
C． 1  x  0 或0  x  1
B． 1  x  0 或 x  1
D． x  1 或0  x  1
【分析】直接利用正比例函数的性质得出 B 点横坐标，再利用函数图象得出 x 的取值范围．
【解答】解：正比例函 y  k x 与反比例函数 y  k2 的图象相交于 A 、B 两点，其中点 A
112x
的横坐标为 1．
 B 点的横坐标为： 1 ，
故当 y1  y2 时， x 的取值范围是： x  1 或0  x  1．
故选： D ．
【点评】此题主要考查了反比例函数与一次函数的交点问题，正确得出 B 点横坐标是解题关键．
9．（3 分）如图，在钝角三角形 ABC 中， AB  6cm ， AC  12cm ，动点 D 从点 A 出发沿 AB以1cm / s 的速度向点 B 运动，同时动点 E 从点 C 出发沿CA 以 2cm / s 的速度向点 A 运动， 当以 A ， D ， E 为顶点的三角形与ABC 相似时，运动时间是( )
A． 3s 或 4.8sB． 3sC． 4.5sD． 4.5s 或 4.8s
【分析】如果以点 A 、 D 、 E 为顶点的三角形与ABC 相似，由于 A 与 A 对应，那么分两种情况：① D 与 B 对应；② D 与C 对应．根据相似三角形的性质分别作答．
【解答】解：如果两点同时运动，设运动t 秒时，以点 A 、D 、 E 为顶点的三角形与ABC
相似，
则 AD  t(cm) ， CE  2t(cm) ， AE  AC  CE  (12  2t )(cm) ，
①当 D 与 B 对应时，有ADE∽ABC ，
 AD : AB  AE : AC ，
t : 6  (12  2t) :12 ，
t  3 ；
②当 D 与C 对应时，有ADE∽ACB ，
 AD : AC  AE : AB ，
t :12  (12  2t) : 6 ，
t  4.8 ，
当以点 A 、 D 、 E 为顶点的三角形与ABC 相似时，运动的时间是 3 秒或 4.8 秒， 故选： A ．
【点评】本题考查了相似三角形的判定，利用分类讨论思想解决问题是本题的关键． 10．（3 分）如图，F 为正方形 ABCD 的边CD 上一动点，AB  2 ，连接 BF ，过 A 作 AH  BF交 BC 于 H ，交 BF 于G ，连接CG ，当CG 为最小值时， CH 的长为()
2
A．B．
C． 3 D． 3 
2 2
5
5
5
【分析】如图 1 中，取 AB 的中点O ，连接OG ，OC ．首先证明O ，G ，C 共线时，CG 的值最小（如图 2 中），证明CF  CG  BH 即可解决问题（图 2 中）．
【解答】解：如图 1 中，取 AB 的中点O ，连接OG ， OC ．
四边形 ABCD 是正方形，
ABC  90 ，
 AB  2 ，
OB  OA  1 ，
OB2  BC2
12  22
5
OC ，
 AH  BF ，
AGB  90 ，
 AO  OB ，
OG  1 AB  1 ，
2
CGOC  OG ，
5
当O ， G ， C 共线时， CG 的值最小，最小值 1 （如图 2 中），
 OB  OG  1 ，
OBG  OGB ，
 AB / /CD ，
OBG  CFG ，
OGB  CGF ，
CGF  CFG ，
5
CF  CG  1 ，
ABH  BCF  AGB  90 ，
BAH  ABG  90 ， ABG  CBF  90 ，
BAH  CBF ，
 AB  BC ，
ABH  BCF (ASA) ，
5
 BH  CF  1 ，
5
CH  BC  BH  2  ( 5  1)  3 ， 故选： C ．
【点评】本题考查正方形的性质，全等三角形的判定和性质，直角三角形斜边中线的性质，
等腰三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决 问题，属于中考选择题中的压轴题．
二、选择题（每小题 3 分，共 6 小题，满分 18 分）
11．（3 分）若关于 x 的一元二次方程 kx2  4x  1  0 有实数根，则 k 的取值范围是 k 4
且 k  0 ．
【分析】根据二次项系数非零结合根的判别式△ 0 ，即可得出关于 k 的一元一次不等式组， 解之即可得出结论．
【解答】解：关于 x 的一元二次方程 kx2  4x  1  0 有实数根，
 k  0 且△  42  4k0 ，
解得： k 4 且 k  0 ．
故答案为： k 4 且 k  0 ．
【点评】本题考查了根的判别式以及一元二次方程的定义，牢记“当△0 时，方程有实数根”是解题的关键．
12．（3 分）函数 y  (m 1)x|m|2 是反比例函数，则 m 的值为 1 ．
【分析】根据反比例函数的定义．即 y  k (k  0) ，只需令|m|2  1 ， m  1  0 即可．
x
【解答】解：由题意得： |m|2  1 且， m  1  0 ； 解得 m  1 ，又 m  1 ；
 m  1 ． 故填 m  1 ．
【点评】本题考查了反比例函数的定义，重点是将一般式 y  k (k  0) 转化为 y  kx1(k  0)
x
的形式．
13．（3 分）如图所示，四边形 ABCD 内接于O ， E 为 AB 延长线上一点， AOC  100 ，则CBE  50 ．
【分析】根据圆周角定理求出ADC ，根据圆内接四边形的性质求出ABC ，再根据邻补角的概念计算，得到答案．
【解答】解：AOC  100 ，
ADC  1 AOC  50 ，
2
四边形 ABCD 内接于O ，
ABC  180  ADC  180  50  130 ，
CBE  180  130  50 ， 故答案为： 50 ．
【点评】本题考查的是圆内接四边形的性质、圆周角定理，掌握圆内接四边形的对角互补是 解题的关键．
14．（3 分）如图所示，将ABC 绕点 A 顺时针旋转 n 度到ADE 的位置， D 在 BC 边上，若
B  60 ，则 n  60度．
【分析】由旋转的性质得 AB  AD ，可证ABD 是等边三角形，从而得出 n  60 ．
【解答】解：将ABC 绕点 A 顺时针旋转 n 度到ADE 的位置，
 AB  AD ，
B  60 ，
ABD 是等边三角形，
BAD  60 ，
 n  60 ，
故答案为：60．
【点评】本题主要考查了旋转的性质，等边三角形的判定与性质等知识，熟练掌握旋转前后 对应边相等是解题的关键．
15．（3 分）飞机着陆后滑行的距离 s （单位： m) 关于滑行的时间t （单位： s) 的函数解析
式是 s  60t  1.5t 2 ，飞机着陆后滑行 600米才能停下来．
【分析】将函数解析式配方成顶点式求出 s 的最大值即可得．
【解答】解： s   3 t 2  60t   3 (t  20)2  600 ，
22
当t  20 时， s 取得最大值 600，即飞机着陆后滑行 600 米才能停下来， 故答案为：600．
【点评】本题主要考查二次函数的应用，理解题意得出飞机滑行的距离即为 s 的最大值是解题的关键．
16．（3 分）抛物线 y  ax2  bx  c 的对称轴是直线 x  1 ，且过点(1, 0) ．顶点位于第二象限，其部分图象如图所示，给出以下判断：① ab  0 且c  0 ；② 4a  2b  c  0 ；③ 8a  c  0 ；
④ c  3a  3b ；⑤直线 y  2x  2 与抛物线 y  ax2  bx  c 两个交点的横坐标分别为 x ， x ，
12
则 x1  x2  x1 x2  5 ．其中结论正确的是 ②④⑤ ．
【分析】根据二次函数的性质一一判断即可．
【解答】解：抛物线对称轴 x  1 ，经过(1, 0) ，
 b
2a
 1 ， a  b  c  0 ，
b  2a ， c  3a ，
 a  0 ，
b  0 ， c  0 ，
 ab  0 且c  0 ，故①错误，
抛物线对称轴 x  1 ，经过(1, 0) ，
(2, 0) 和(0, 0) 关于对称轴对称，
 x  2 时， y  0 ，
 4a  2b  c  0 ，故②正确，
抛物线与 x 轴交于(3, 0) ，
 x  4 时， y  0 ，
16a  4b  c  0 ，
 b  2a ，
16a  8a  c  0 ，即8a  c  0 ，故③错误，
 c  3a  3a  6a ， b  2a ，
c  3a  3b ，故④正确，
直线 y  2x  2 与抛物线 y  ax2  bx  c 两个交点的横坐标分别为 x ， x ，
12
方程 ax2  (b  2)x  c  2  0 的两个根分别为 x ， x ，
 x  x
  b  2 ， x  x
12
 c  2 ，
12a12a
 x  x  x x
  b  2  c  2   2a  2  3a  2  5 ，故⑤正确，

121 2
aaaa
故答案为②④⑤．
【点评】本题考查二次函数与系数的关系，二次函数图象上的点的特征，解题的关键是灵活 运用所学知识解决问题，属于中考常考题型．
三、解答题（本大题共 9 小题，满分 102 分，解答应写出文字说明、证明过程或演算步骤）
17．（8 分）解方程： x2  2x ．
【分析】原方程有公因式 x ，先提取公因式，然后再分解因式求解．
【解答】解： x2  2x ，
 x2  2x  0 ，
 x(x  2)  0 ，
 x  0 或 x  2  0 ，
 x1  0 ， x2  2 ．
【点评】考查了解一元二次方程  因式分解法，只有当方程的一边能够分解成两个一次因式， 而另一边是 0 的时候，才能应用因式分解法解一元二次方程．分解因式时，要根据情况灵活运用学过的因式分解的几种方法．
18．（8 分）如图，点C 、D 在线段 AB 上，PCD 是等边三角形，且ACP∽PDB ，求APB
的度数．
【分析】根据等边三角形的性质得到 PCD  60 ， 根据相似三角形的判定定理证明
ACP∽ABP ，根据相似三角形的性质得到答案．
【解答】解：PCD 是等边三角形，
PCD  60 ，
ACP  120 ，
ACP∽PDB ，
APC  B ，又A  A ，
ACP∽ABP ，
APB  ACP  120 ．
【点评】本题考查的是相似三角形的判定和性质，掌握相似三角形的对应角相等是解题的关
键．
19．（10 分）如图，点O ， B 的坐标分别是(0, 0) ， (3, 0) ．将OAB 绕点O 逆时针旋转90 ，得到△ OA1B1 ．
画出平面直角坐标系和三角形△ OA1B1 ；
求旋转过程中点 B 走过的路径的长．
【分析】（1）利用旋转变换的性质分别作出 A ， B 的对应点 A1 ， B1 即可；
（2）利用弧长公式求解即可．
【解答】解：（1）如图，三角形△ OA1B1 即为所求；
（2） OB  3 ，
点 B 走过的路径的长 90 3  3 ．
1802
【点评】本题考查作图 旋转变换，弧长公式等知识，解题的关键是掌握旋转变换的性质， 记住弧长公式l  nr ．
180
20．（10 分）二次函数图象上部分点的横坐标 x ，纵坐标 y 的对应值如表：
求这个二次函数的表达式；
在图中画出这个二次函数的图象；
x

4
3
2
1
0
1
2

y

5
0
3
4
3
0
5

当函数值 y  0 时，对应的 x 的取值范围是3  x  1 ．
【分析】（1）利用表中数据和抛物线的对称性可得到二次函数的顶点坐标为(1, 4) ，则可设顶点式 y  a(x  1)2  4 ，然后把点(0, 3) 代入求出 a 即可；
利用描点法画二次函数图象；
观察函数图象即可求解．
【解答】解：（1）由题意可得二次函数的顶点坐标为 (1, 4) ，设二次函数的解析式为： y  a(x  1)2  4 ，
把点(0, 3) 代入 y  a(x  1)2  4 得 a  1 ，
抛物线解析式为 y  (x  1)2  4 ；
如图所示：
观察函数图象知， y  0 时， x 的取值范围是3  x  1 ， 故答案为： 3  x  1 ．
【点评】本题考查了用待定系数法求二次函数的解析式：在利用待定系数法求二次函数关系
式时，要根据题目给定的条件，选择恰当的方法设出关系式，从而代入数值求解．数形结合
是解题的关键．
步数
频数
频率
0x  4000
8
0.16
4000x  8000
15
0.3
8000x  12000
12
a
12000x  16000
b
0.2
16000x  20000
3
0.06
20000x  24000
2
0.04
21．（12 分）随着“微信运动”被越来越多的人关注和喜爱，某数学兴趣小组随机调查了我区 50 名教师某日“微信运动”中的步数情况进行统计整理，绘制了如下的统计图表（不完整）:
请根据以上信息，解答下列问题：
写出 a ， b 的值并补全频数分布直方图；
我市约有 5000 名教师，用调查的样本数据估计日行走步数超过 12000 步（包含 12000
步）的教师有多少名？
若在 50 名被调查的教师中，选取日行走步数超过 16000 步（包含 16000 步）的两名教
师与大家分享心得，用树形图或列表法求被选取的两名教师恰好都在 20000 步（包含 20000
步）以上的概率．
【分析】（1）根据频率  频数 总数可得 a 、b 的值；
用总人数乘以样本中第 4、5、6 组的频率之和即可得；
步数超过 16000 步（包含 16000 步）的三名教师用 A 、 B 、C 表示，步数超过 20000
步（包含 20000 步）的两名教师用 a 、b 表示，画树状图列出所有等可能结果，从中找到符合条件的结果数，再根据概率公式计算可得．
【解答】解：（1） a  12  50  0.24 ， b  50  0.2  10 ，补全频数分布直方图如下：
（2） 5000  (0.2  0.06  0.04)  1500 ，
答：估计日行走步数超过 12000 步（包含 12000 步）的教师有 1500 名；
（3）步数超过 16000 步（包含 16000 步）的三名教师用 A 、 B 、C 表示，步数超过 20000
步（包含 20000 步）的两名教师用 a 、b 表示， 画树状图为：
共有 20 种等可能的结果数，其中被选取的两名教师恰好都在 20000 步（包含 20000 步）以
上的结果数为 2，
所以被选取的两名教师恰好都在 20000 步（包含 20000 步）以上的概率
2  1 ．
2010
【点评】本题考查了列表法与树状图法：利用列表法或树状图法展示所有可能的结果求出 n ， 再从中选出符合事件 A 或 B 的结果数目 m ，然后根据概率公式计算事件 A 或事件 B 的概 率．也考查了统计图．
22．（12 分）疫情肆虐，万众一心．由于医疗物资极度匮乏，许多工厂都积极宣布生产医疗物资以应对疫情．某工厂及时引进了 1 条口罩生产线生产口罩，开工第一天生产 300 万个，
第三天生产 432 万个，若每天生产口罩的个数增长的百分率相同，请解答下列问题：
每天增长的百分率是多少？
经调查发现，一条生产线最大产能是 900 万个/ 天，如果每增加 1 条生产线，每条生产线的最大产能将减少 30 万个/ 天．现该厂要保证每天生产口罩 3900 万个，在增加产能同时又要节省投入的条件下（生产线越多，投入越大），应该增加几条生产线？
【分析】（1）设每天增长的百分率是 x ，利用第三天的产量 第一天的产量(1  每天增长
的百分率） 2 ，即可得出关于 x 的一元二次方程，解之取其正值即可得出结论；
（2）设应该增加 y 条生产线，则每条生产线的最大产能为(900  30 y) 万个/ 天，根据该厂要保证每天生产口罩 3900 万个，即可得出关于 y 的一元二次方程，解之即可得出 y 值，再结合要节省投入，即可得出应该增加 4 条生产线．
【解答】解：（1）设每天增长的百分率是 x ，依题意得： 300(1  x)2  432 ，
解得： x1  0.2  20% ， x2  2.2 （不合题意，舍去）．
答：每天增长的百分率是 20% ．
（2）设应该增加 y 条生产线，则每条生产线的最大产能为(900  30 y) 万个/ 天， 依题意得： (900  30 y)(1  y)  3900 ，
整理得： y2  29 y  100  0 ， 解得： y1  4 ， y2  25 ．
又要节省投入，
 y  4 ．
答：应该增加 4 条生产线．
【点评】本题考查了一元二次方程的应用，找准等量关系，正确列出一元二次方程是解题的 关键．
23．（12 分）如图，一次函数 y  x  b 与反比例函数 y   k (x  0) 的图象交于点 A(m, 4) 和
x
B(4,1) ．
求b 、 k 、 m 的值；
根据图象直接写出x  b   k (x  0) 的解集；
x
点 P 是线段 AB 上一点，过点 P 作 PD  x 轴于点 D ，连接OP ，若POD 的面积为 S ，求 S 的最大值和最小值．
【分析】（1）将 B(4,1) 代入 y  x  b 得b  5 ，即得一次函数的解析式为 y  x  5 ，将 B(4,1)
代入 y   k 得 k  4 ，即得反比例函数的解析式为 y  4 ；
xx
（2）求出 A(1, 4) ，由图可得，  k  x  b 得解集为： 0  x  1或 x  4 ；
x
（ 3 ） 由 点 P 是 线 段 AB 上 一 点 ， 可 设 设
P(n, n  5)
， 且 1n4
， 可 得
S  1 OD  PD   1 (n  5 )2  25 ，即得当 n  5 时， S 有最大值 25 ，且最大值是 2，当 n  1
222828
或 n  4 时， S 有最小值，且最小值是 2．
【解答】解：（1）将 B(4,1) 代入 y  x  b 得：
1  4  b ，解得b  5 ，
一次函数的解析式为 y  x  5 ，
将 B(4,1) 代入 y   k 得：
x
1   k ，解得 k  4 ，
4
反比例函数的解析式为 y  4 ；
x
将 A(m, 4) 代入 y  x  5 得：
4  m  5 ，解得 m  1，
 A(1, 4) ，
b  5 ， k  4 ， m  1．
由图可得，  k  x  b 得解集为： 0  x  1或 x  4 ；
x
点 P 是线段 AB 上一点，设 P(n, n  5) ，
1n4 ，
 S  1 OD  PD  1  n(n  5)   1 (n2  5n)   1 (n  5 )2  25 ，
222228
 1  0 ，且1n4 ，
2
当 n  5 时， S 有最大值，且最大值是 25 ，
28
当 n  1 或 n  4 时， S 有最小值，且最小值是 2．
【点评】本题考查一次函数与反比例函数的综合应用，涉及待定系数法、不等式解集、三角 形面积等知识，解题的关键是用含 n 的代数式表示 S ．
24．（15 分）如图，四边形 ABCD 内接于O ，AC 为直径，AC 和 BD 交于点 E ，AB  BC ．
求ADB 的度数；
过 B 作 AD 的平行线，交 AC 于 F ，试判断线段 EA ， CF ， EF 之间满足的等量关系， 并说明理由；
在（2）条件下过 E ， F 分别作 AB ， BC 的垂线，垂足分别为G ， H ，连接GH ，交
BO 于 M ，若 AG  3 ， S四边形AGMO : S四边形CHMO  8 : 9 ，求O 的半径．
【分析】（1）由直径所对的圆周角为直角及等腰三角形的性质和互余关系可得答案；
线段 EA ，CF ，EF 之间满足的等量关系为：EA2  CF 2  EF 2 ．如图 2，设ABE  ，
CBF   ， 先证明  45 ， 再过 B 作 BN  BE ， 使 BN  BE ， 连接 NC ， 判定
AEB  CNB(SAS ) 、 BFE  BFN (SAS ) ， 然 后 在 RtNFC 中 ， 由 勾 股 定 理 得 ：
CF 2  CN 2  NF 2 ，将相关线段代入即可得出结论；
ABC矩形BGKH
如图 3，延长GE ，HF 交于 K ，由（2）知 EA2  CF 2  EF 2 ，变形推得 S S，
SBGM  S四边形COMH ，SBMH  S四边形AGMO ，结合已知条件 S四边形AGMO : S四边形CHMO  8 : 9 ，设 BG  9k ，
BH  8k ，则 CH  3  k ，求得 AE 的长，用含 k 的式子表示出 CF 和 EF ，将它们代入
EA2  CF 2  EF 2 ，解得 k 的值，则可求得答案．
【解答】解：（1）如图 1，
 AC 为直径，
ABC  90 ，
ACB  BAC  90 ，
 AB  BC ，
ACB  BAC  45 ，
ADB  ACB  45 ；
线段 EA ， CF ， EF 之间满足的等量关系为： EA2  CF 2  EF 2 ．理由如下： 如图 2，设ABE  ， CBF  ，
 AD / / BF ，
EBF  ADB  45 ， 又ABC  90 ，
  45 ，
过 B 作 BN  BE ，使 BN  BE ，连接 NC ，
 AB  CB ， ABE  CBN ， BE  BN ，
AEB  CNB (SAS ) ，
 AE  CN ， BCN  BAE  45 ，
FCN  90 ．
FBN    FBE ， BE  BN ， BF  BF ，
BFE  BFN (SAS ) ，
 EF  FN ，
在RtNFC 中， CF 2  CN 2  NF 2 ，
 EA2  CF 2  EF 2 ；
如图 3，延长GE ， HF 交于 K ，
由（2）知 EA2  CF 2  EF 2 ，
 1 EA2  1 CF 2  1 EF 2 ，
222
 SAGE  SCFH  SEFK ，
 SAGE  SCFH  S五边形BGEFH  SEFK  S五边形BGEFH ，
即 SABC  S矩形BGKH ，
 1 S
2
ABC
 1 S
2
矩形BGKH ，
 SGBH  SABO  SCBO ，
 SBGM  S四边形COMH ， SBMH  S四边形AGMO ，
 S四边形AGMO : S四边形CHMO  8 : 9 ，
 SBMH : SBGM  8 : 9 ，
 BM 平分GBH ，
 BG : BH  9 : 8 ，
设 BG  9k ， BH  8k ，
CH  3  k ，
 AG  3 ，
2
 AE  3，
CF 
2(k  3) ， EF 
2(8k  3) ，
 EA2  CF 2  EF 2 ，
 (3 2)2 [ 2(k  3)]2  [ 2(8k  3)]2 ，
整理得： 7k 2  6k 1  0 ，
解得： k   1 （舍去）， k  1 ．
172
 AB  12 ，
 AO 
2 AB  6，
2
2
2
O 的半径为6．
【点评】本题属于圆的综合题，考查了圆的相关性质及定理、全等三角形的判定与性质、多 边形的面积公式、勾股定理及解一元二次方程等知识点，熟练运用相关性质及定理是解题的 关键．
25．（15 分）已知抛物线 y  ax2  bx  c(a  0) 与 x 轴交于 A(1, 0) 、 B 两点，与 y 轴交于点
C(0, 3a) ．
求点 B 的坐标；
若 a  1 ， 点 M 和点 N 在抛物线上，且 M 的横坐标为 4， 点 N 在第二象限，若
2
AMN  2OAM ，求点 N 的坐标；
（3）P 是第四象限内抛物线上的一个动点，直线 PA 、PB 分别交 y 轴于点 M 、N ，判断CM 与CN 的数量关系，并说明理由．
c  3a
【分析】（ 1 ） 由 A(1, 0) 、 C(0, 3a) 在抛物线 y  ax2  bx  c 上， 可得 b  2a ， 即有

y  ax2  2ax  3a ，令 y  0 ，得 ax2  2ax  3a  0 ，而 a  0 ，可得 B(3, 0) ；
（2）连接 AM 交 y 轴于 D ，过 M 作 ME / / x 轴交 y 轴于 E ，在 y 轴上取 F ，使 EF  ED ，
作直线 MF 交抛物线于 N ， 根据 EMA  OAM
， EM 是 DF 的垂直平分线， 可证
AMN  2AME  2OAM ，而 a  1 时，抛物线为 y  1 x2  x  3 ，知 M (4, 5 ) ，直线 AM
2222
D(0, )
F (0, )
的解析式为 y  1 x  1 ，可求出1 ，从而求出 EF  DE  2 ，9 ，即可得直线 MF
2222
 y   1 x  9
为 y   1 x  9 ，最后由 22得 N (3, 6) ；


22 y 

1 x2  x  3
22
（ 3 ） 结 论 ：
CN  3CM
， 设 P(m, am2  2am  3a)
， 可 得 直 线 PA 解 析 式 为
y  (am  3a)x  am  3a ，从而得到 M (0, am  3a) ，即有 CM  am ，同理可得 CN  3am ， 故CN  3CM ．
【解答】解：（1） A(1, 0) 、C(0, 3a) 在抛物线 y  ax2  bx  c 上，
 0  a  b  c ，可得b  2a ，


3a  cc  3a
 y  ax2  2ax  3a ，
令 y  0 ，得 ax2  2ax  3a  0 ，而 a  0 ， 解得 x  1 或 x  3 ，
 B(3, 0) ；
连接 AM 交 y 轴于 D ，过 M 作 ME / / x 轴交 y 轴于 E ，在 y 轴上取 F ，使 EF  ED ， 作直线 MF 交抛物线于 N ，如图：
由作图可知： EMA  OAM ，直线 EM 是 DF 的垂直平分线，
FME  DME ，
AMN  2AME  2OAM ，
而 a  1 时，抛物线为 y  1 x2  x  3 ，
222
 M 的横坐标为 4，
5
 M (4, ) ，
2
由 A(1, 0) ， M (4, 5 ) 得直线 AM 的解析式为 y  1 x  1 ，
222
令 x  0 得 y  1 ，
2
1
 D(0, ) ，
2
 ME / / x 轴，
5
 E(0, ) ，
2
 EF  DE  2 ，
9
 F (0, ) ，
2
M (4, )
设直线 MF 为 y  kx  9 ，将5 代入得： 5  4k  9 ，
2222
 k   1 ，
2
直线 MF 为 y   1 x  9 ，
22
 y   1 x  9
x  4
由
22
13
x  3
得：或
 y  6 y  5
（舍去），

 y 

x2  x 
22
2
 N (3, 6) ；
CN  3CM ，理由如下： 设 P(m, am2  2am  3a) ，如图：
设直线 PA 解析式为 y  sx  t ，
am2  2am  3a  ms  t
则0  s  t

，解得s  am  3a ，

t  am  3a
直线 PA 解析式为 y  (am  3a)x  am  3a ， 令 x  0 得 y  am  3a ，
 M (0, am  3a) ， 而C(0, 3a) ，
CM  am ，
设直线 PB 解析式为 y  sx  t ，
0  3s  ts  am  a
则am2  2am  3a  s m  t  ，解得t  3am  3a ，

直线 PB 解析式为 y  (am  a)x  3am  3a ， 令 x  0 得 y  3am  3a ，
 N (0, 3am  3a) ， 而C(0, 3a) ，
CN  3am ，
CN  3CM ．
【点评】本题考查二次函数综合应用，涉及待定系数法、函数图象上点坐标的特征、数形结 合等知识，解题的关键是用含字母的代数式表示相关点的坐标及相关线段的长度．