2022-2023学年广东省广州八十九中九年级（上）期末数学试卷（含答案）

这是一份2022-2023学年广东省广州八十九中九年级（上）期末数学试卷（含答案），共26页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
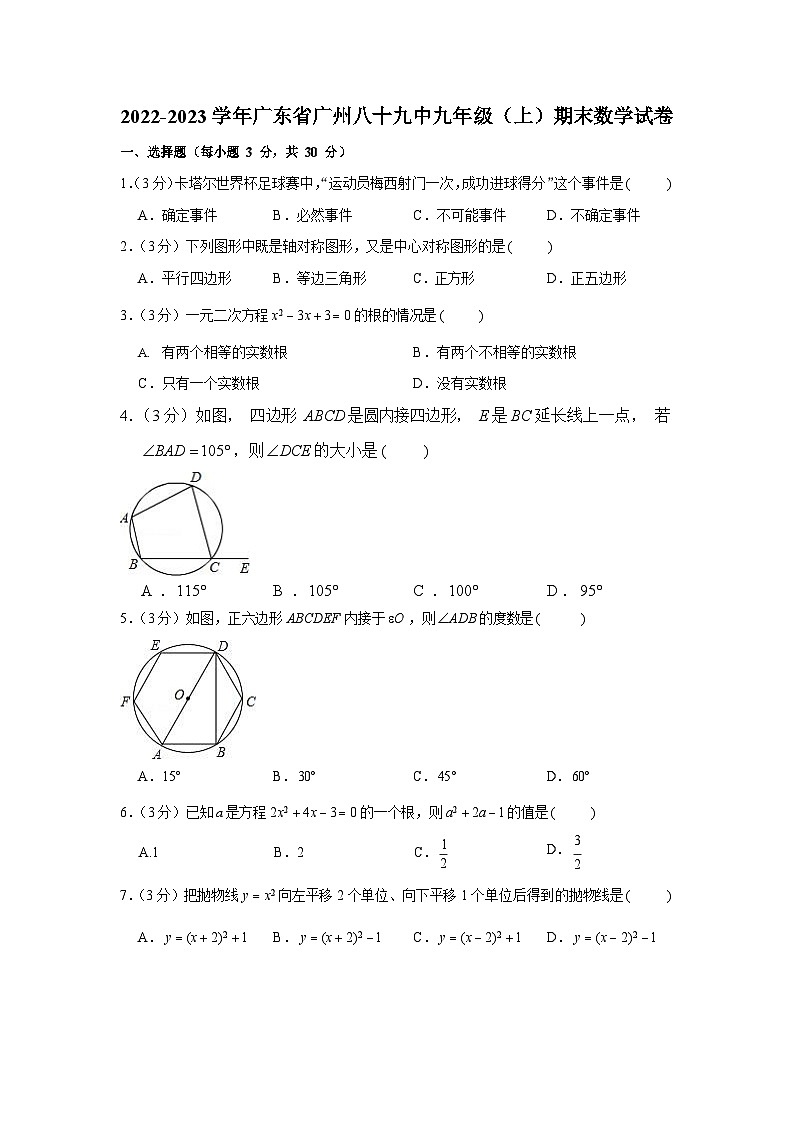
1．（3 分）卡塔尔世界杯足球赛中，“运动员梅西射门一次，成功进球得分”这个事件是()
A．确定事件B．必然事件C．不可能事件D．不确定事件2．（3 分）下列图形中既是轴对称图形，又是中心对称图形的是( )
A．平行四边形B．等边三角形C．正方形D．正五边形3．（3 分）一元二次方程 x2  3x  3  0 的根的情况是()
有两个相等的实数根B．有两个不相等的实数根
C．只有一个实数根D．没有实数根
4．（3 分）如图， 四边形 ABCD 是圆内接四边形， E 是 BC 延长线上一点， 若
BAD  105 ，则DCE 的大小是()
A ．115B ．105C ．100D ． 95
5．（3 分）如图，正六边形 ABCDEF 内接于O ，则ADB 的度数是()
A．15B． 30C． 45D． 60
6．（3 分）已知 a 是方程 2x2  4x  3  0 的一个根，则 a2  2a  1 的值是()
B．2C． 1 2
D． 3
2
7．（3 分）把抛物线 y  x2 向左平移 2 个单位、向下平移 1 个单位后得到的抛物线是()
A． y  (x  2)2  1
B． y  (x  2)2 1
C． y  (x  2)2  1
D． y  (x  2)2 1
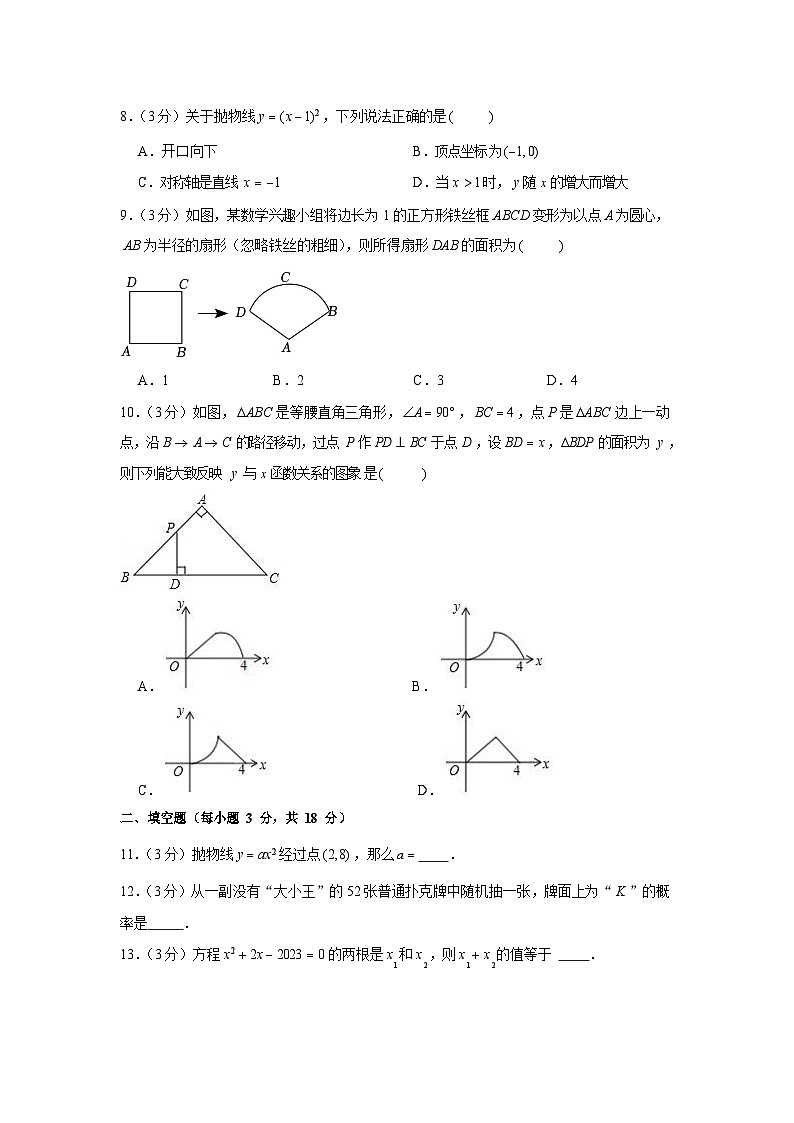
8．（3 分）关于抛物线 y  (x 1)2 ，下列说法正确的是()
A．开口向下B．顶点坐标为(1, 0)
C．对称轴是直线 x  1D．当 x  1 时， y 随 x 的增大而增大
9．（3 分）如图，某数学兴趣小组将边长为 1 的正方形铁丝框 ABCD 变形为以点 A 为圆心，
AB 为半径的扇形（忽略铁丝的粗细），则所得扇形 DAB 的面积为()
A．1B．2C．3D．4
10．（3 分）如图， ABC 是等腰直角三角形， A  90 ， BC  4 ，点 P 是ABC 边上一动点，沿 B  A  C 的路径移动，过点 P 作 PD  BC 于点 D ，设 BD  x ，BDP 的面积为 y ， 则下列能大致反映 y 与 x 函数关系的图象是()
A． B．
C． D．
二、填空题（每小题 3 分，共 18 分）
11．（3 分）抛物线 y  ax2 经过点(2,8) ，那么 a  ．
12．（3 分）从一副没有“大小王”的 52 张普通扑克牌中随机抽一张，牌面上为“ K ”的概率是．
13．（3 分）方程 x2  2x  2023  0 的两根是 x 和 x ，则 x  x 的值等于 ．
1212
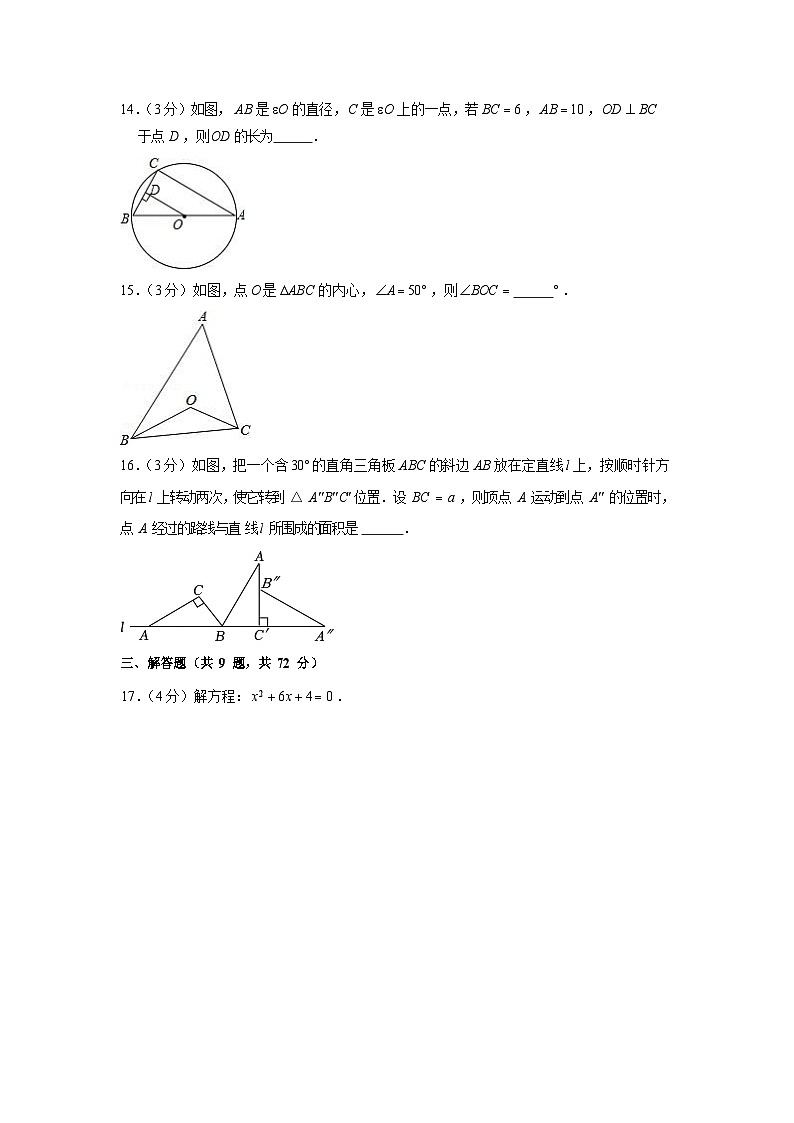
14．（3 分）如图， AB 是O 的直径， C 是O 上的一点，若 BC  6 ， AB  10 ， OD  BC
于点 D ，则OD 的长为．
15．（3 分）如图，点O 是ABC 的内心， A  50 ，则BOC   ．
16．（3 分）如图，把一个含30 的直角三角板 ABC 的斜边 AB 放在定直线l 上，按顺时针方向在l 上转动两次，使它转到△ ABC 位置．设 BC  a ，则顶点 A 运动到点 A 的位置时， 点 A 经过的路线与直线l 所围成的面积是．
三、解答题（共 9 题，共 72 分）
17．（4 分）解方程： x2  6x  4  0 ．
18．（10 分）如图：在平面直角坐标系中，点 A 、 B 、C 都在格点上
画出 ABC 关于原点对称的△ A1 B1C1 ，并写出 A 、B 、C 三点关于原点对称的坐标 A1 、
B1 、C1 ．
画出ABC 绕原点O 顺时针方向旋转90 得到的△ A2 B2C2 ，并求点 A 运动到 A2 的轨迹的弧长．
19．（5 分）如图，AB 是O 的直径，点C 、D 是O 上的两点，且 AC  CD ．求证：OC / / BD ．
20．（5 分）如图，在 ABC 中，BAC  120 ，以 BC 为边向形外作等边三角形 BCD ，把 ABD
绕着点 D 按顺时针方向旋转 60 后得到ECD （点 A ， C ， E 三点共线）．
ADE 的度数为．
若 AB  3 ， AC  2 ，求 DE 的长．
21．（9 分）在一个不透明的袋子中，装有除颜色外其余均相同的红、蓝两种球，已知其中红球有 3 个，且从中任意摸出一个红球的概率为 0.75．
根据题意，袋中有个蓝球；
若第一次随机摸出一球，不放回，再随机摸出第二个球，请用画树状图或列表法求“ 摸到两球中至少一个球为蓝球（记为事件 A) ”的概率 P （A）．
22．（9 分）如图，在 RtABC 中，ABC  90 ，以 AB 为直径作半圆O 交 AC 于点 D ，点 E
为 BC 中点，连接 DE ．
求证： DE 是半圆O 的切线；
若BAC  30 ， DE  1 ，求 AD 的长．
23．（10 分）如图，某学校要建一个中间有两道篱笆隔断的长方形花圃，花圃的一边靠墙（墙的最大可利用长度为10m) ，现有篱笆长 24m ．设花圃的宽 AB 为 x m ，面积为 S m2 ．
如果要围成面积为32m2 的花圃， AB 长是多少米？
能围成面积比32m2 更大的花园吗？如果能，请求出花圃的最大面积，并给出设计方案．如果不能，请说明理由．
24．（10 分）如图，在RtABC 中， C  90 ， BAC  30 ． D 是线段CA 延长线上的任意一点．连接 BD ，以点 B 为中心，将线段 BD 顺时针旋转60 ，得到线段 BE ，连接 AE ．
依题意补全图形，探究线段 AE 、 BE 的数量关系，并给予证明；
若 AB  a(a  0) 为常数，试用 a 表示 AE 2  CD2 的值．
25．（10 分）如图，抛物线 y  ax2  2x  3a 经过 A(1, 0) 、 B(b, 0) 、C(0, c) 三点．
求 a ， b ， c 的值；
在抛物线对称轴上找出一点 P ，使 PA  PC 的值最小，并求出此时ACP 的面积；
若点 M 为 x 轴上一动点，抛物线上是否存在一点 N ，使以 A ， C ， M ， N 四点构成的四边形为平行四边形？若存在，请直接写出点 N 的坐标；若不存在，请说明理由．
2022-2023 学年广东省广州八十九中九年级（上）期末数学试卷
参考答案与试题解析
一、选择题（每小题 3 分，共 30 分）
1．（3 分）卡塔尔世界杯足球赛中，“运动员梅西射门一次，成功进球得分”这个事件是()
A．确定事件B．必然事件C．不可能事件D．不确定事件
【解答】解：卡塔尔世界杯足球赛中，“运动员梅西射门一次，成功进球得分”这个事件是不确定事件，
故选： D ．
2．（3 分）下列图形中既是轴对称图形，又是中心对称图形的是()
A．平行四边形B．等边三角形C．正方形D．正五边形
【解答】解： A ．平行四边形是中心对称图形，不是轴对称图形，故此选项不合题意；
B ．等边三角形是轴对称图形，不是中心对称图形，故此选项不合题意； C ．正方形既是轴对称图形，又是中心对称图形，故此选项符合题意； D ．正五边形是轴对称图形，不是中心对称图形，故此选项不合题意． 故选： C ．
3．（3 分）一元二次方程 x2  3x  3  0 的根的情况是()
有两个相等的实数根B．有两个不相等的实数根
C．只有一个实数根D．没有实数根
【解答】解： x2  3x  3  0 ，
△  (3)2  4 1 3  3  0 ，
方程没有实数根． 故选： D ．
4．（3 分）如图， 四边形 ABCD 是圆内接四边形， E 是 BC 延长线上一点， 若
BAD  105 ，则DCE 的大小是()
A ．115B ．105C ．100D ． 95
【解答】解： 四边形 ABCD 是圆内接四边形，
BAD  BCD  180， 而BCD  DCE  180 ，
DCE  BAD ， 而BAD  105 ，
DCE  105． 故选： B ．
5．（3 分）如图，正六边形 ABCDEF 内接于O ，则ADB 的度数是()
A．15B． 30C． 45D． 60
【解答】解：连接OB ，
多边形 ABCDEF 是正多边形，
AOB  360  60 ，
6
ADB  1 AOB  1  60  30 ．
22
故选： B ．
6．（3 分）已知 a 是方程 2x2  4x  3  0 的一个根，则 a2  2a  1 的值是()
B．2C． 1 2
D． 3
2
【解答】解： a 是方程 2x2  4x  3  0 的一个根，
 2a2  4a  3  0 ，
整理得， a2  2a  3 ，
2
 a2  2a  1  3  1  1 ，
22
故选： C ．
7．（3 分）把抛物线 y  x2 向左平移 2 个单位、向下平移 1 个单位后得到的抛物线是()
A． y  (x  2)2  1
B． y  (x  2)2 1
C． y  (x  2)2  1
D． y  (x  2)2 1
【解答】解：原抛物线的顶点为(0, 0) ，向左平移 2 个单位，再向下平移 1 个单位，那么新抛物线的顶点为(2, 1) ．
可设新抛物线的解析式为 y  (x  2)2 1． 故选： B ．
8．（3 分）关于抛物线 y  (x 1)2 ，下列说法正确的是()
A．开口向下B．顶点坐标为(1, 0)
C．对称轴是直线 x  1D．当 x  1 时， y 随 x 的增大而增大
【解答】解： A ，由抛物线可看出 a  1  0 ，故开口向上，不符合题意；
B ，抛物线的顶点坐标是(1, 0) ，不符合题意．
C ，抛物线的对称轴是直线 x  1 ，错误，不符合题意；
D ，由于开口方向向上，对称轴为直线 x  1 ， x  1 时 y 随 x 的增大而增大，正确，符合题意；
故选： D ．
9．（3 分）如图，某数学兴趣小组将边长为 1 的正方形铁丝框 ABCD 变形为以点 A 为圆心，
AB 为半径的扇形（忽略铁丝的粗细），则所得扇形 DAB 的面积为()
A．1B．2C．3D．4
【解答】解：正方形的边长为 1，
 BD 的长度 2 ，
 S扇形DAB
 1 lr  1  2 1  1 ．
22
故选： A ．
10．（3 分）如图， ABC 是等腰直角三角形， A  90 ， BC  4 ，点 P 是ABC 边上一动点，沿 B  A  C 的路径移动，过点 P 作 PD  BC 于点 D ，设 BD  x ，BDP 的面积为 y ， 则下列能大致反映 y 与 x 函数关系的图象是()
A． B．
C． D．
【解答】解：过 A 点作 AH  BC 于 H ，
ABC 是等腰直角三角形，
B  C  45 ， BH  CH  AH  1 BC  2 ，
2
当0x2 时，如图 1，
B  45 ，
 PD  BD  x ，
 y  1  x  x  1 x2 ；
22
当 2  x4 时，如图 2，
C  45 ，
 PD  CD  4  x ，
 y  1  (4  x)  x   1 x2  2x ，
22
故选： B ．
二、填空题（每小题 3 分，共 18 分）
11．（3 分）抛物线 y  ax2 经过点(2,8) ，那么 a  2．
【解答】解：抛物线 y  ax2 经过点(2,8) ，
点(2,8) 满足抛物线方程 y  ax2 ，
8  4a ，解得， a  2 ； 故答案为：2．
12．（3 分）从一副没有“大小王”的 52 张普通扑克牌中随机抽一张，牌面上为“ K ”的概
率是1．
13
【解答】解：因为没有大、小王的扑克牌共有 52 张，其中数为“ K ”的共 4 种情况，
随机抽取一张，牌面上数为“ K ”的概率是 4  1 ．
故答案为： 1 ．
13
5213
13．（3 分）方程 x2  2x  2023  0 的两根是 x 和 x ，则 x  x 的值等于 2 ．
1212
【解答】解：方程 x2  2x  2023  0 的二次项系数 a  1 ，一次项系数b  2 ，
 x  x   b   2  2 ．
12a1
故答案为： 2 ．
14．（3 分）如图， AB 是O 的直径， C 是O 上的一点，若 BC  6 ， AB  10 ， OD  BC
于点 D ，则OD 的长为 4．
【解答】解： OD  BC ，
 BD  CD  1 BC  3 ，
2
 OB  1 AB  5 ，
2
OB2  BD2
OD 
 4 ．
故答案为 4．
15．（3 分）如图，点O 是ABC 的内心， A  50 ，则BOC  115  ．
【解答】解：点O 是ABC 的内心，
ABO  OBC ， ACO  OCB ，
A  50 ，
ABC  ACB  130 ，
ABO  ACO  OBC  OCB  65 ， 则BOC  180  65  115 ．
故答案为：115．
16．（3 分）如图，把一个含30 的直角三角板 ABC 的斜边 AB 放在定直线l 上，按顺时针方向在l 上转动两次，使它转到△ ABC 位置．设 BC  a ，则顶点 A 运动到点 A 的位置时，
点 A 经过的路线与直线l 所围成的面积是
25a2  3 a2．
122
【解答】解：由题意知：
90 ( 3a)2
120 (2a)21
S  a 3a 3603602
 4a2  3a2  3 a2
342
 25a2  3 a2 ．
122
故答案为： 25a2  3 a2 ．
122
三、解答题（共 9 题，共 72 分）
17．（4 分）解方程： x2  6x  4  0 ．
【解答】解：这里 a  1 ， b  6 ， c  4 ，
△  b2  4ac  36  16  20 ，
5
 x  6  2 5  3，
2
5
5
则 x1  3 ， x2   3 ．
18．（10 分）如图：在平面直角坐标系中，点 A 、 B 、C 都在格点上
画出 ABC 关于原点对称的△ A1 B1C1 ，并写出 A 、B 、C 三点关于原点对称的坐标 A1 、
B1 、C1 ．
画出ABC 绕原点O 顺时针方向旋转90 得到的△ A2 B2C2 ，并求点 A 运动到 A2 的轨迹的弧长．
【解答】解：（1）如图所示：△ A1 B1C1 即为所求， A1 (2,1) ， B1 (3, 3) ， C1 (0, 4) ；
（2）如图所示：△ A B C 即为所求，点 A 运动到 A 的轨迹的弧长为： 90 5  5 ．
2 2 2
21802
19．（5 分）如图，AB 是O 的直径，点C 、D 是O 上的两点，且 AC  CD ．求证：OC / / BD ．
【解答】证明： AC  CD ，
 AC  DC ，
ABC  DBC ，
OC  OB ，
OCB  OBC ，
OCB  DBC ，
OC / / BD ．
20．（5 分）如图，在 ABC 中，BAC  120 ，以 BC 为边向形外作等边三角形 BCD ，把 ABD
绕着点 D 按顺时针方向旋转 60 后得到ECD （点 A ， C ， E 三点共线）．
ADE 的度数为60 ．
若 AB  3 ， AC  2 ，求 DE 的长．
【解答】解：（1）把 ABD 绕着点 D 按顺时针方向旋转60 后得到ECD （点 A ， C ， E
三点共线），
 AD  DE ， EC  AB ， ADE  60 ； 故答案为： 60 ；
（2） AD  DE ， ADE  60 ，
ADE 是等边三角形，
 ED  AE  AC  CE  AC  AB  3  2  5 ．
21．（9 分）在一个不透明的袋子中，装有除颜色外其余均相同的红、蓝两种球，已知其中红球有 3 个，且从中任意摸出一个红球的概率为 0.75．
根据题意，袋中有 1个蓝球；
若第一次随机摸出一球，不放回，再随机摸出第二个球，请用画树状图或列表法求“ 摸到两球中至少一个球为蓝球（记为事件 A) ”的概率 P （A）．
【解答】解：（1）设袋中有 x 个蓝球，
根据题意得 3
x  3
 0.75 ，解得 x  1 ，
即袋中有 1 个蓝球． 故答案为 1；
（2）画树状图为：
共有 12 种等可能的结果数，其中两球中至少一个球为蓝球的结果数为 6 种，
所以 P （A）  6  1 ．
122
22．（9 分）如图，在 RtABC 中，ABC  90 ，以 AB 为直径作半圆O 交 AC 于点 D ，点 E
为 BC 中点，连接 DE ．
求证： DE 是半圆O 的切线；
若BAC  30 ， DE  1 ，求 AD 的长．
【解答】（1）证明：连接OD 、OE 、 BD ，如图所示：
 AB 为圆O 的直径，
ADB  BDC  90 ，
在RtBDC 中， E 为斜边 BC 的中点，
 DE  BE ，
在OBE 和ODE 中，


OB  OD OE  OE ，

BE  DE
OBE  ODE (SSS ) ，
ODE  ABC  90 ， 又 OD 为半径，
 DE 为圆O 的切线；
（2）解：在RtABC 中， BAC  30 ，
 BC  1 AC ，
2
 BC  2DE  2 ，
 AC  4 ，
又C  60 ， DE  CE ，
DEC 为等边三角形，即 DC  DE  1 ， 则 AD  AC  DC  3 ．
23．（10 分）如图，某学校要建一个中间有两道篱笆隔断的长方形花圃，花圃的一边靠墙（墙的最大可利用长度为10m) ，现有篱笆长 24m ．设花圃的宽 AB 为 x m ，面积为 S m2 ．
如果要围成面积为32m2 的花圃， AB 长是多少米？
能围成面积比32m2 更大的花园吗？如果能，请求出花圃的最大面积，并给出设计方案．如果不能，请说明理由．
【解答】解：（1） BC  24  4x ，
 S  x(24  4x)  4x2  24x ， 当 S  32 时， 4x2  24x  32 ， 解得 x1  2 ， x2  4 ，
墙的最大可利用长度为10m ，
 0  24  4x10, 7 x  6 ，
2
 x1  2 （舍去）， x2  4 ，
即花圃的宽 AB 为 4m ，
答：如果要围成面积为32m2 的花圃， AB 的长是 4 米．
（2）能围成面积比32m2 更大的花圃，
 S  4x2  24x  4(x  3)2  36 ，
当 x  3 时， S 随 x 的增大而减小，
 7 x  6 ，
2
 当x  7 时, S
2最大
 4( 7  3)2  36  35  32
2
能围成面积比32m2 更大的花圃，最大面积为35m2 ，
方案： 24  4  7  10 ，
2
花圃的长为 10 米，宽为 3.5 米，
答：能围成面积比32m2 更大的花圃，最大面积是35m2 ，方案是花圃的长为 10 米，宽为 3.5
米．
24．（10 分）如图，在RtABC 中， C  90 ， BAC  30 ． D 是线段CA 延长线上的任意一点．连接 BD ，以点 B 为中心，将线段 BD 顺时针旋转60 ，得到线段 BE ，连接 AE ．
依题意补全图形，探究线段 AE 、 BE 的数量关系，并给予证明；
若 AB  a(a  0) 为常数，试用 a 表示 AE 2  CD2 的值．
【解答】解：（1）如图，
AE  BE ．
理由如下：作 EH  AB 于 H 点，如图，
C  90 ， BAC  30 ，
 AB  2BC ， ABC  60 ，
线段 BD 顺时针旋转60 ，得到线段 BE ，
 BE  BD ， DBE  60 ，
ABC  DBA  DBE  DBA ， 即DBC  EBH ，
在DBC 和EBH 中，
C  BHE

DBC  EBH ，

DB  EB
DBC  EBH (AAS ) ，
 BC  BH ，
 AB  2BC ，
 AH  BH ，
 EH 垂直平分 AB ，
 AE  BE ；
（2）连接 DE ，如图，
线段 BD 顺时针旋转60 ，得到线段 BE ，
 BE  BD ， DBE  60 ，
BDE 为等边三角形，
 DB  BE ，
 BE  AE ，
 BE  AE ， 在RtDBC 中，
 DB2  CD2  BC 2 ，
 DB2  CD2  a2 ，
 AE 2  CD2  a2 ．
25．（10 分）如图，抛物线 y  ax2  2x  3a 经过 A(1, 0) 、 B(b, 0) 、C(0, c) 三点．
求 a ， b ， c 的值；
在抛物线对称轴上找出一点 P ，使 PA  PC 的值最小，并求出此时ACP 的面积；
若点 M 为 x 轴上一动点，抛物线上是否存在一点 N ，使以 A ， C ， M ， N 四点构成的四边形为平行四边形？若存在，请直接写出点 N 的坐标；若不存在，请说明理由．
【解答】解：（1）把 A(1, 0) 代入抛物线 y  ax2  2x  3a ，可得： a  2  3a  0 ，
解得 a  1 ．
抛物线的解析式为： y  x2  2x  3 ；
把 B(b, 0) ， C(0, c) 代入 y  x2  2x  3 ， 可得： b  1 或b  3 ， c  3 ，
 A(1, 0) ，
b  3 ．
 a  1 ， b  3 ， c  3 ；
抛物线的解析式为： y  x2  2x  3 ，
其对称轴为直线 x   b
2a
连接 BC ，如图 1 所示，
 1，
 B(3, 0) ， C(0, 3) ，
设直线 BC 的解析式为 y  kx  3(k  0) ，
3k  3  0 ， 解得 k  1 ，
直线 BC 的解析式为 y  x  3 ，
当 x  1 时， y  1  3  2 ，
 P(1, 2) ，
ACP 的面积 ABC 的面积ABP 的面积 1  (3  1)  3  1  (3  1)  2  2 ；
22
存在点 N ，使以 A ， C ， M ， N 四点构成的四边形为平行四边形．
如图 2 所示，
①当点 N 在 x 轴下方时，
抛物线的对称轴为直线 x  1 ， C(0, 3) ，
 N (2, 3) ；
②当点 N 在 x 轴上方时，
如图 2，过点 N  作 N D  x 轴于点 D ， 在△ AN D 与△ M CO 中，
N DA  COM 

CM A  N AD ，

 AN   CM 
△ AN D  △ M CO(AAS ) ，
 N D  OC  3 ，即 N  点的纵坐标为 3．
3  x2  2x  3 ，
7
7
解得 x  1 或 x  1 ，
7
7
 N (1 ， 3) ， N “ (1 ， 3) ．
7
7
综上所述，符合条件的点 N 的坐标为(2, 3) ， (1 ， 3) 或(1 ， 3) ．