2022-2023学年广东省广州市海珠区中山大学附中九年级（上）期末数学试卷（含答案）

这是一份2022-2023学年广东省广州市海珠区中山大学附中九年级（上）期末数学试卷（含答案），共28页。试卷主要包含了下列事件是必然事件的是等内容，欢迎下载使用。
1．（3 分）下列图形中，是中心对称图形但不是轴对称图形的是()
A．等边三角形B．圆C．矩形D．平行四边形2．（3 分）抛物线 y  2(x  4)2  3 顶点坐标是()
A． (4,3)B． (4, 3)
C． (4, 3)
D． (3, 4)
3．（3 分）下列事件是必然事件的是()
太阳从东方升起
汽车累计行驶 1 万千米，从未出现故障
姚明在罚球线上投篮一次，投中 D．经过有交通信号灯的路口，遇到绿灯
4．（3 分）已知 x  1 是关于 x 的一元二次方程 x2  mx  0 的一个根，则 m 的值是()
A． 1
B．0C．1D．2
5．（3 分）已知反比例函数图象经过点(2, 3) 当 y  3 时， x 的取值范围是()
x  2
x  2 或 x  0
x  2
x  0
6．（3 分）如图，在平面直角坐标系中，ABC 与DEF 是以原点O 为位似中心的位似图形，若 A(2, 0) ， D(3, 0) ， BC  3 ，则 EF 的长为()
A．2B．4.5C．4D．6
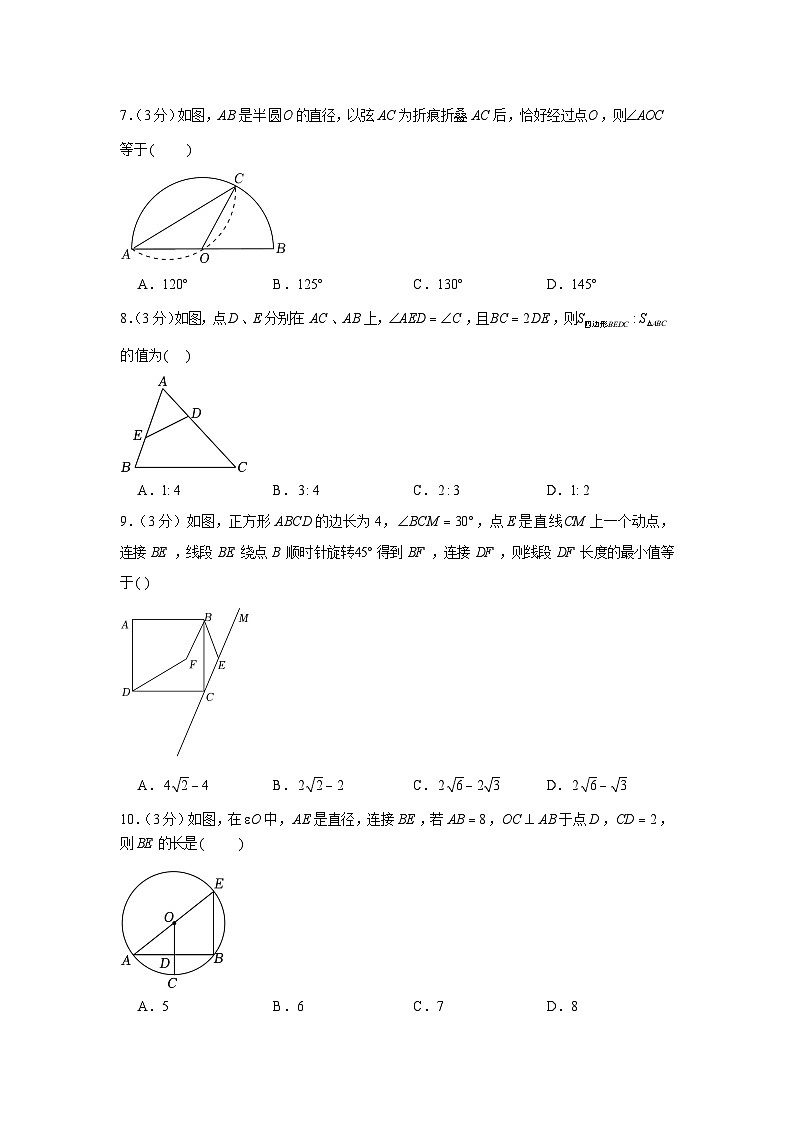
7．（3 分）如图，AB 是半圆O 的直径，以弦 AC 为折痕折叠 AC 后，恰好经过点O ，则AOC
等于()
A．120B．125C．130D．145
8．（3 分）如图，点 D 、E 分别在 AC 、AB 上，AED  C ，且 BC  2DE ，则 S四边形BEDC : SABC
的值为( )
A．1: 4B． 3 : 4C． 2 : 3D．1: 2
9．（3 分）如图，正方形 ABCD 的边长为 4， BCM  30 ，点 E 是直线CM 上一个动点，连接 BE ，线段 BE 绕点 B 顺时针旋转45 得到 BF ，连接 DF ，则线段 DF 长度的最小值等于( )
2
A． 4 4
B． 2 2
C． 2 2
D． 2
2
6
3
6
3
10．（3 分）如图，在O 中， AE 是直径，连接 BE ，若 AB  8 ，OC  AB 于点 D ，CD  2 ，则 BE 的长是()
A．5B．6C．7D．8
二．填空题（本大题共 6 小题，每小题 3 分，共 18 分）
11．（3 分）平面直角坐标系中，一点 P(2, 3) 关于原点的对称点 P 的坐标是 ．
12．（3 分）圆锥的底面半径为 2，母线长为 6，则它的侧面积为 ．
1
13．（3 分）已知二次函数 y  ax2  bx  c(a  0) 图象的对称轴为直线 x  1 ，且经过点(1, y ) ，
(0, y2 ) ，则 y1 y2 （填“  ”“  ”或“  ” )
14．（3 分）在某一时刻，测得一根高为1.2m 的竹竿的影长为3m ，同时测得一栋楼的影长为
60m ，则这栋楼的高度为m ．
15．（3 分）在平面直角坐标系中，以点(3, 2) 为圆心，3 为半径的圆与 y 轴的位置关系为．
16．（3 分）如图，AB 是半圆直径，半径OC  AB 于点O ，AD 平分CAB 交弧 BC 于点 D ，连接CD 、OD ，给出以下四个结论：① AC / /OD ；② CE  OE ；③ ODE∽ADO ；④ 2CD2  CEAB ．其中正确结论的序号是．
三．解答题（本大题共 9 小题，满分 72 分，解答应写出文字说明、证明过程或演算步骤）
17．（4 分）解方程： (2x 1)2  4 ．
18．（4 分）如图，在平面直角坐标系中，ABC 三个顶点的坐标分别为 A(2, 2) ，B(3, 2) ，
C(1, 0) ．
在平面直角坐标系中，点 P 的坐标为(1, 1) ，请在平面直角坐标系中画出ABC 关于点 P 成中心对称的新图形△ A1B1C1 ．
请直接写出以O 为位似中心，△ A2 B2C2 与ABC 位似比为 2 :1 时顶点 A2 的坐标．
19．（6 分）如图，正比例函数 y  x 的图象与反比例函数 y  k (x  0) 的图象交于点 A(1, a) ，
x
在ABC 中， ACB  90 ， CA  CB ，点C 坐标为(2, 0) ．
求 k 的值；
求 AB 所在直线的解析式．
20．（6 分）“双减”政策下，为了切实提高课后服务质量，红星中学开展了丰富多彩的课后服务活动，设置了体育活动、劳动技能、经典阅读、科普活动四大板块课程（依次记为 A ， B ， C ， D) ．若该校小慧和小丽随机选择一个板块课程．
小慧选科普活动课程的概率是；
用画树状图或列表的方法，求小慧和小丽选同一个板块课程的概率．
21．（8 分）已知关于 x 的一元二次方程 x2  2mx  m2  m  0 有实数根．
求 m 的取值范围；
若该方程的两个实数根分别为 x 、 x ，且 x2  x2  12 ，求 m 的值．
1212
22．（10 分）如图，在RtABC 中， ACB  90 ， CD 是斜边 AB 上的中线，以CD 为直径
的O 分别交 AC 、 BC 于点 M 、 N ，过点 N 作 NE  AB ，垂足为点 E ．
若O 的半径为13 ， AC  5 ，求 BN 的长；
4
求证： NE 是O 的切线．
23．（10 分）某旅游景点的门票价格是 20 元/ 人，日接待游客 500 人，进入旅游旺季时，景点想提高门票价格增加盈利．经过市场调查发现，门票价格每提高 5 元，日接待游客人数就 会减少 50 人．设提价后的门票价格为 x （元/ 人） (x  20) ，日接待游客的人数为 y （人) ．
求 y 与 x(x  20) 的函数关系式；
已知景点每日的接待成本为 z （元) ， z 与 y 满足函数关系式是 z  100  10 y ．求景点的门票价格为多少元时，每日获取的利润为 7900 元？（利润 门票收入 接待成本）
24．（12 分）如图，正方形 ABCD 和正方形 DEFG 有公共顶点 D ．
如图 1，连接 AG 和CE ，直接写出 AG 和CE 的数量及位置关系；
如图 2，连接 AE ， M 为 AE 中点，连接 DM 、CG ，探究 DM 、CG 的数量及位置关系，并说明理由；
25．（12 分）已知抛物线 y  ax2  bx  c 与 x 轴交于 A(2, 0) 、 B(6, 0) 两点，与 y 轴交于点
C(0, 3) ．
求抛物线的表达式；
点 P 为直线 BC 下方的抛物线上一个动点，当PBC 面积最大时，求点 P 的坐标；
点 P 在直线 BC 下方的抛物线上，连接 AP 交 BC 于点 M ，当 PM 最大时，求点 P 的
AM
横坐标及 PM 的最大值．
AM
2022-2023 学年广东省广州市海珠区中山大学附中九年级（上） 期末数学试卷
参考答案与试题解析
一．选择题（本大题共 10 小题，每小题 3 分，共 30 分）
1．（3 分）下列图形中，是中心对称图形但不是轴对称图形的是()
A．等边三角形B．圆C．矩形D．平行四边形
【解答】解：等边三角形不是中心对称图形，是轴对称图形， A 不合题意； 圆是中心对称图形，也是轴对称图形， B 不合题意；
矩形是中心对称图形，是轴对称图形， C 不合题意；
平行四边形是中心对称图形但不是轴对称图形， D 符合题意， 故选： D ．
2．（3 分）抛物线 y  2(x  4)2  3 顶点坐标是()
A． (4,3)B． (4, 3)
C． (4, 3)
D． (3, 4)
【解答】解：抛物线顶点式解析式为： y  2(x  4)2  3 ，
顶点坐标为(4,3) ， 故选： A ．
3．（3 分）下列事件是必然事件的是()
太阳从东方升起
汽车累计行驶 1 万千米，从未出现故障
姚明在罚球线上投篮一次，投中 D．经过有交通信号灯的路口，遇到绿灯
【解答】解： A ．太阳从东方升起，这是必然事件，故 A 符合题意；
B ．汽车累计行驶 1 万千米，从未出现故障，这是随机事件，故 B 不符合题意；
C ．姚明在罚球线上投篮一次，投中，这是随机事件，故C 不符合题意；
D ．经过有交通信号灯的路口，遇到绿灯，这是随机事件，故 D 不符合题意． 故选： A ．
4．（3 分）已知 x  1 是关于 x 的一元二次方程 x2  mx  0 的一个根，则 m 的值是()
A． 1
B．0C．1D．2
【解答】解：把 x  1 代入方程 x2  mx  0 得： 1  m  0 ， 解得： m  1．
故选： A ．
5．（3 分）已知反比例函数图象经过点(2, 3) 当 y  3 时， x 的取值范围是()
x  2
x  2 或 x  0
x  2
x  0
【解答】解：把(2, 3) 代入 y  k 得 k  2  3  6 ，
x
反比例函数的图象位于二、四象限，在每个象限 y 随 x 的增大而增大，
把 y  3 代入 y   6 ，得3   6 ，
xx
解得 x  2 ，
当 y  3 时， x 的取值范围是 x  2 或 x  0 ． 故选： B ．
6．（3 分）如图，在平面直角坐标系中，ABC 与DEF 是以原点O 为位似中心的位似图形，若 A(2, 0) ， D(3, 0) ， BC  3 ，则 EF 的长为()
A．2B．4.5C．4D．6
【解答】解： A(2, 0) ， D(3, 0) ，
OA  2 ， OD  3 ，
OA : OD  2 : 3 ，
ABC 与DEF 是以坐标原点O 为位似中心的位似图形，
ABC∽DEF ，
 BC : EF  OA : OD  2 : 3 ，
 BC  3 ，
 EF  4.5 ， 故选： B ．
7．（3 分）如图，AB 是半圆O 的直径，以弦 AC 为折痕折叠 AC 后，恰好经过点O ，则AOC
等于()
A．120B．125C．130D．145
【解答】解： O 关于直线 AC 的对称点是Q ，连接OQ ，交 AC 于 M ，
则 AC 垂直平分OQ ，
即 AQ  AO ， OM  AC ，
 OQ  OA ，
OQ  AQ  OA ，
AQO 是等边三角形，
AOQ  60 ，
 OQ  AC ， OA  OC ，
COQ  AOQ  60 ，
AOC  60  60  120 ， 故选： A ．
8．（3 分）如图，点 D 、E 分别在 AC 、AB 上，AED  C ，且 BC  2DE ，则 S四边形BEDC : SABC
的值为()
A．1: 4B． 3 : 4C． 2 : 3D．1: 2
【解答】解：AED  C ， A  A ，
AED∽ACB ，
 BC  2DE ，
 SADE  ( DE )2 
( 1 )2  1 ，
SABCBC24
 S四边形BEDC : SABC  3 : 4 ， 故选： B ．
9．（3 分）如图，正方形 ABCD 的边长为 4， BCM  30 ，点 E 是直线CM 上一个动点，连接 BE ，线段 BE 绕点 B 顺时针旋转45 得到 BF ，连接 DF ，则线段 DF 长度的最小值等于( )
2
A． 4 4
B． 2 2
C． 2 2
D． 2
2
6
3
6
3
【解答】解：如图，连接 BD ，在 BD 上截取 BG ，使得 BG  BC ，连接 FG ，过点 D 作 DH  GF
于点 H ．
四边形 ABCD 是正方形，
CBD  45 ， CD  CB  4 ， DCB  90 ，
2
 BD  4， BG  BC  4 ，
2
 DG  BD  BG  4 4 ，
CBG  EBF  45 ，
CBE  GBF ， 在CBE 和GBF 中，
CB  GB

CBE  GBF ，

BE  BF
CBE  GBF (SAS ) ，
BCE  BGF  30 ，
点 F 在直线GF 上运动，当点 F 与 H 重合时， DF 的值最小，
 DH  FH ， DGH  BGF  30
2
 DH  1 DG  2
2
 DF 的最小值为 2
 2 ，
2
 2 ，
故选： B ．
10．（3 分）如图，在O 中， AE 是直径，连接 BE ，若 AB  8 ，OC  AB 于点 D ，CD  2 ，则 BE 的长是()
A．5B．6C．7D．8
【解答】解： OC 是O 的半径， OC  AB ，
 AD  1 AB  4 ．
2
在RtADO 中，
设OC  OA  x ，则OD  x  2 ． 由勾股定理，得 x2  (x  2)2  42 ，
解得 x  5 ，即OA  5 ．
 AE  2  OA  10 ．
 AE 是直径，
B  90 ． 在RtABE 中，
AE2  AB2
 BE 
102  82

 6 ．
故选： B ．
二．填空题（本大题共 6 小题，每小题 3 分，共 18 分）
11．（3 分）平面直角坐标系中，一点 P(2, 3) 关于原点的对称点 P 的坐标是 (2, 3) ．
【解答】解：根据中心对称的性质，得点 P(2, 3) 关于原点对称点 P 的坐标是(2, 3) ． 故答案为： (2, 3) ．
12．（3 分）圆锥的底面半径为 2，母线长为 6，则它的侧面积为 12 ．
【解答】解：根据圆锥的侧面积公式：rl   2  6  12， 故答案为：12．
1
13．（3 分）已知二次函数 y  ax2  bx  c(a  0) 图象的对称轴为直线 x  1 ，且经过点(1, y ) ，
(0, y2 ) ，则 y1  y2 （填“  ”“  ”或“  ” )
【解答】解：二次函数 y  ax2  bx  c(a  0) 图象的对称轴为直线 x  1 ，
当 x  1 时， y 随 x 的增大而增大，当 x  1 时， y 随 x 的增大而减小，
该函数经过点(1, y1 ) ， (0, y2 ) ， | 1 1| 2 ， | 0  1 | 1 ，
 y1  y2 ，
故答案为：  ．
14．（3 分）在某一时刻，测得一根高为1.2m 的竹竿的影长为3m ，同时测得一栋楼的影长为
60m ，则这栋楼的高度为 24m ．
【解答】解：设这栋楼的高度为 h m ，
在某一时刻，测得一根高为1.2m 的竹竿的影长为3m ，同时测得一栋楼的影长为60m ，
 1.2  h ，
360
解得 h  24 ． 故答案为：24．
15．（3 分）在平面直角坐标系中，以点(3, 2) 为圆心，3 为半径的圆与 y 轴的位置关系为 相
切 ．
【解答】解：点(3, 2) 到 y 轴的距离为 3，且以点(3, 2) 为圆心的圆的半径为 3，
点(3, 2) 到 y 轴的距离等于圆的半径，
该圆与 y 轴的位置关系是相切， 故答案为：相切．
16．（3 分）如图，AB 是半圆直径，半径OC  AB 于点O ，AD 平分CAB 交弧 BC 于点 D ，连接CD 、OD ，给出以下四个结论：① AC / /OD ；② CE  OE ；③ ODE∽ADO ；④ 2CD2  CEAB ．其中正确结论的序号是 ①④ ．
【解答】解：① AB 是半圆直径，
 AO  OD ，
OAD  ADO ，
 AD 平分CAB 交弧 BC 于点 D ，
CAD  DAO  1 CAB ，
2
CAD  ADO ，
 AC / /OD ，
①正确．
②过点 E 作 EF  AC ，
 OC  AB ， AD 平分CAB 交弧 BC 于点 D ，
OE  EF ，
在RtEFC 中， CE  EF ，
CE  OE ，
②错误．
③在ODE 和ADO 中，只有ADO  EDO ，
COD  2CAD  2OAD ，
DOE  DAO ，
不能证明ODE 和ADO 相似，
③错误；
④ AD 平分CAB 交弧 BC 于点 D ，
CAD  1  45  22.5 ，
2
COD  45 ，
 AB 是半圆直径，
OC  OD ，
OCD  ODC  67.5
CAD  ADO  22.5 （已证），
CDE  ODC  ADO  67.5  22.5  45 ，
CED∽CDO ，
 CD  CE ，
COCD
CD2  OCCE  1 ABCE ，
2
 2CD2  CEAB ．
④正确．
综上所述，只有①④正确． 故答案为：①④．
三．解答题（本大题共 9 小题，满分 72 分，解答应写出文字说明、证明过程或演算步骤）
17．（4 分）解方程： (2x 1)2  4 ．
【解答】解：(2x 1)2  4 ，
 2x  1  2 ，
 2x  1  2 或 2x  1  2 ，
 x  3 ， x   1 ．
1222
18．（4 分）如图，在平面直角坐标系中，ABC 三个顶点的坐标分别为 A(2, 2) ，B(3, 2) ，
C(1, 0) ．
在平面直角坐标系中，点 P 的坐标为(1, 1) ，请在平面直角坐标系中画出ABC 关于点 P 成中心对称的新图形△ A1B1C1 ．
） 请直接写出以 O 为位似中心， △ A2 B2C2 与 ABC 位似比为 2 :1 时顶点 A2 的坐标
(4, 4) 或(4, 4) ．
【解答】解：（1）如图，△ A1 B1C1 为所作；
（2）利用△ A2 B2C2 与ABC 位似比为 2 :1 ，
 A2 (4, 4) 或(4, 4) ．
故答案为： (4, 4) 或(4, 4) ．
19．（6 分）如图，正比例函数 y  x 的图象与反比例函数 y  k (x  0) 的图象交于点 A(1, a) ，
x
在ABC 中， ACB  90 ， CA  CB ，点C 坐标为(2, 0) ．
求 k 的值；
求 AB 所在直线的解析式．
【解答】解：（1）正比例函数 y  x 的图象经过点 A(1, a) ，
 a  1 ，
 A(1,1) ，
点 A 在反比例函数 y  k (x  0) 的图象上，
x
 k  11  1 ；
（2）作 AD  x 轴于点 D ， BE  x 轴于点 E ，
 A(1,1) ， C(2, 0) ，
 AD  1 ， CD  3 ，
ACB  90 ，
ACD  BCE  90 ，
ACD  CAD  90 ，
BCE  CAD ， 在BCE 和CAD 中，
BCE  CAD

BEC  CDA  90 ，

CB  AC
BCE  CAD(AAS ) ，
CE  AD  1 ， BE  CD  3 ，
 B(3, 3) ，
设直线 AB 的解析式为 y  mx  n ，
m   1
 m  n  1
3m  n  3

，解得 2 ，


n  3
2
直线 AB 的解析式为 y   1 x  3 ．
22
20．（6 分）“双减”政策下，为了切实提高课后服务质量，红星中学开展了丰富多彩的课后服务活动，设置了体育活动、劳动技能、经典阅读、科普活动四大板块课程（依次记为 A ， B ， C ， D) ．若该校小慧和小丽随机选择一个板块课程．
小慧选科普活动课程的概率是1；
4
用画树状图或列表的方法，求小慧和小丽选同一个板块课程的概率．
【解答】解：（1）小慧选科普活动课程的概率是 1 ，
4
故答案为： 1 ；
4
（2）画树状图如下：
共有 16 种等可能的结果，其中小慧和小丽选同一个板块课程的结果有 4 种，
小慧和小丽选同一个板块课程的概率为 4  1 ．
164
21．（8 分）已知关于 x 的一元二次方程 x2  2mx  m2  m  0 有实数根．
求 m 的取值范围；
若该方程的两个实数根分别为 x 、 x ，且 x2  x2  12 ，求 m 的值．
1212
【解答】解：（1）根据题意得△  (2m)2  4(m2  m)0 ，
解得 m0 ．
故 m 的取值范围是 m0 ；
（2）根据题意得 x  x  2m ， x x
 m2  m ，
121 2
121212
 x2  x2  (x  x )2  2x  x  12 ，
(2m)2  2(m2  m)  12 ，即 m2  m  6  0 ， 解得 m1  2 ， m2  3 （舍去）．
故 m 的值为2 ．
22．（10 分）如图，在RtABC 中， ACB  90 ， CD 是斜边 AB 上的中线，以CD 为直径的O 分别交 AC 、 BC 于点 M 、 N ，过点 N 作 NE  AB ，垂足为点 E ．
若O 的半径为13 ， AC  5 ，求 BN 的长；
4
求证： NE 是O 的切线．
【解答】解：（1）连接 DN ， ON ，
O 的半径为13 ，
4
CD  13 ，
2
ACB  90 ， CD 是斜边 AB 上的中线，
 BD  CD  AD  13 ．
2
 AB  13 ，
AB2  AC2
 BC  12 ，
 CD 为直径，
CND  90 ，且 BD  CD ．
 BN  NC  6 ．
（2）ACB  90 ， D 为斜边的中点，
CD  DA  DB  1 AB ．
2
BCD  B ，
 OC  ON ，
BCD  ONC ．
ONC  B ．
ON / / AB ，
 NE  AB ，
ON  NE ．
 NE 为O 的切线．
23．（10 分）某旅游景点的门票价格是 20 元/ 人，日接待游客 500 人，进入旅游旺季时，景点想提高门票价格增加盈利．经过市场调查发现，门票价格每提高 5 元，日接待游客人数就 会减少 50 人．设提价后的门票价格为 x （元/ 人） (x  20) ，日接待游客的人数为 y （人) ．
求 y 与 x(x  20) 的函数关系式；
已知景点每日的接待成本为 z （元) ， z 与 y 满足函数关系式是 z  100  10 y ．求景点的门票价格为多少元时，每日获取的利润为 7900 元？（利润 门票收入 接待成本）
【解答】解：（1）根据题意得： y  500  20  x  50  10x  700 ，
5
 y 与 x(x  20) 的函数关系式为 y  10x  700 ；
（2） z  100  10 y  100  10(10x  700)  100x  7100 ，
 x(10x  700)  (100x  7100)  7900 ， 解得 x  50 或 x  30 ，
景点的门票价格为 50 元或 30 元时，每日获取的利润为 7900 元，
24．（12 分）如图，正方形 ABCD 和正方形 DEFG 有公共顶点 D ．
） 如图 1， 连接 AG 和 CE ， 直接写出 AG 和 CE 的数量及位置关系 AG  CE 且
AG  CE ；
如图 2，连接 AE ， M 为 AE 中点，连接 DM 、CG ，探究 DM 、CG 的数量及位置关系，并说明理由；
【解答】解：（1） AG  CE 且 AG  CE ，理由如下：
四边形 ABCD 和四边形 DEFG 是正方形，
ADC  GDE  90 ， AD  CD ， DG  DE ，
ADG  CDE ，
ADG  CDE (SAS ) ，
 AG  CE ，
ADC  GDE  90 ， 由旋转可知： AG  CE ； 故 AG  CE 且 AG  CE ；
（2） DM 、CG 的关系是： DM  1 CG ，且 DM  CG ，理由如下：
2
如图 2，延长 AD 至 H ，使 AD  DH ，连接 EH ，
GDE  CDH  90 ，
GDE  CDE  CDH  CDE ，即CDG  HDE ，
 CD  DH ， GD  DE ，
DGC  DEH (SAS ) ，
CG  EH ，
 M 是 AE 的中点， AD  DH ，
 DM 是AEH 的中位线，
 DM / / EH ， DM  1 EH ，
2
 DM  1 CG ，
2
GDE  CDH  90 ，
DGC 绕点逆时针旋转90 到DEH ，
CG  EH ，
 DM  CG ．
 DM 、CG 的关系是： DM  1 CG ，且 DM  CG ．
2
25．（12 分）已知抛物线 y  ax2  bx  c 与 x 轴交于 A(2, 0) 、 B(6, 0) 两点，与 y 轴交于点
C(0, 3) ．
求抛物线的表达式；
点 P 为直线 BC 下方的抛物线上一个动点，当PBC 面积最大时，求点 P 的坐标；
点 P 在直线 BC 下方的抛物线上，连接 AP 交 BC 于点 M ，当 PM 最大时，求点 P 的
AM
横坐标及 PM 的最大值．
AM
【解答】解：（1）将点 A(2, 0) 、 B(6, 0) 、C(0, 3) 代入 y  ax2  bx  c ，
a  1
4a  2b  c  04
得36a  6b  c  0 ，解得： b  1 ，


c  3
 y  1 x2  x  3 ；
4


c  3

设直线l 交 BC 于点 H ，
设直线 BC 的解析式为 y  kx  d ，
6k  d  0
k  1

 d  3
，解得： 2 ，

 y  1 x  3 ，
2
d  3
设 P(t, 1 t 2  t  3) ，则 H (t, 1 t  3) ，
4
则PBC 面积 S
PHB
2
SPHC
 1  PH  BO 1  3  1 t 2  t  3)   3 t 2  9 t ，
3( t
22442
  3  0 ，故PBC 面积有最大值，
4
当t  3 时， PBC 面积有最大值，此时点 P(3,  15) ；
4
如图 1，过点 A 作 AE  x 轴交直线 BC 于点 E ，过 P 作 PF  x 轴交直线 BC 于点 F ，
 PF / / AE ，
 MP  PF ，
AMAE
设 P(t, 1 t 2  t  3) ，则 F (t, 1 t
 3) ，
42
 PF  1 t  3  1 t 2  t  3   1 t 2  3 t ，
2442
 A(2, 0) ，
 E(2, 4) ，
 AE  4 ，
 MP  PE 
 1 t 2  3 t
42
  1 (t  3)2 
9  9 ，
AMAE4161616
当t  3 时， MP 有最大值 9 ，
AM16
 P(3,  15) ，
4
即点 P 的横坐标为 3， MP 有最大值 9 ．
AM16