

2022-2023学年广东省广州市荔湾区真光中学九年级(上)期末数学试卷(含答案)
展开
这是一份2022-2023学年广东省广州市荔湾区真光中学九年级(上)期末数学试卷(含答案),共30页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
1.(3 分)一元二次方程3x2 x 2 0 的二次项系数是 3,它的一次项系数是()
1
2
C.1D.0
2.(3 分)如图所示,将矩形纸片 ABCD 折叠,使点 D 与点 B 重合,点C 落在点C 处,折痕为 EF ,若ABE 20 ,那么EFC 的度数为()
A.115B.120C.125D.130 3.(3 分)一元二次方程 x2 2(3x 2) (x 1) 0 的一般形式是()
A. x2 5x 5 0
B. x2 5x 5 0
C. x2 5x 5 0
D. x2 5 0
4.(3 分)“凤鸣”文学社在学校举行的图书共享仪式上互赠图书,每个同学都把自己的图书向本组其他成员赠送一本,某组共互赠了 210 本图书,如果设该组共有 x 名同学,那么依题意,可列出的方程是( )
A. x(x 1) 210
B. x(x 1) 210
C. 2x(x 1) 210
D. 1 x(x 1) 210
2
5.(3 分)在一个不透明的布袋中,红色、黑色、白色的玻璃球共有 40 个,除颜色外其他完全相同,小明通过多次摸球试验后发现其中摸到红色球、黑色球的频率稳定在15% 和45% ,则口袋中白色球的个数可能是( )
A.24B.18C.16D.6
6.(3 分)路边有一根电线杆 AB 和一块长方形广告牌,有一天小明突然发现在太阳光照射下,电线杆顶端 A 的影子刚好落在长方形广告牌的上边中点G 处,而长方形广告牌的影子刚好落在地面上 E 点(如图),已知 BC 5 米,长方形广告牌的长 HF 4 米,高 HC 3 米, DE 4 米,则电线杆 AB 的高度是()
A.6.75 米B.7.75 米C.8.25 米D.10.75 米
7.(3 分)如图,在正方形 ABCD 中,点 E 为 AB 边的中点,点 F 在 DE 上, CF CD ,过点 F 作 FG FC 交 AD 于点 G .下列结论:① GF GD ;② AG AE ;③ AF DE ;④ DF 4EF .正确的是( )
A.①②B.①③C.①③④D.③④
8.(3 分)设 x , x 是一元二次方程 x2 2x 3 0 的两根,则 x2 x2 ()
1212
A.2B. 2
1
D.10
9.(3 分)若关于 x 的方程 x2 2x m 1 0 有两个实根 x 、 x ,则 x x (x2 x2 ) 2x2 4x
121 2 1211
的最大值是(
)
A.3
B.4
C.4.5
D.5
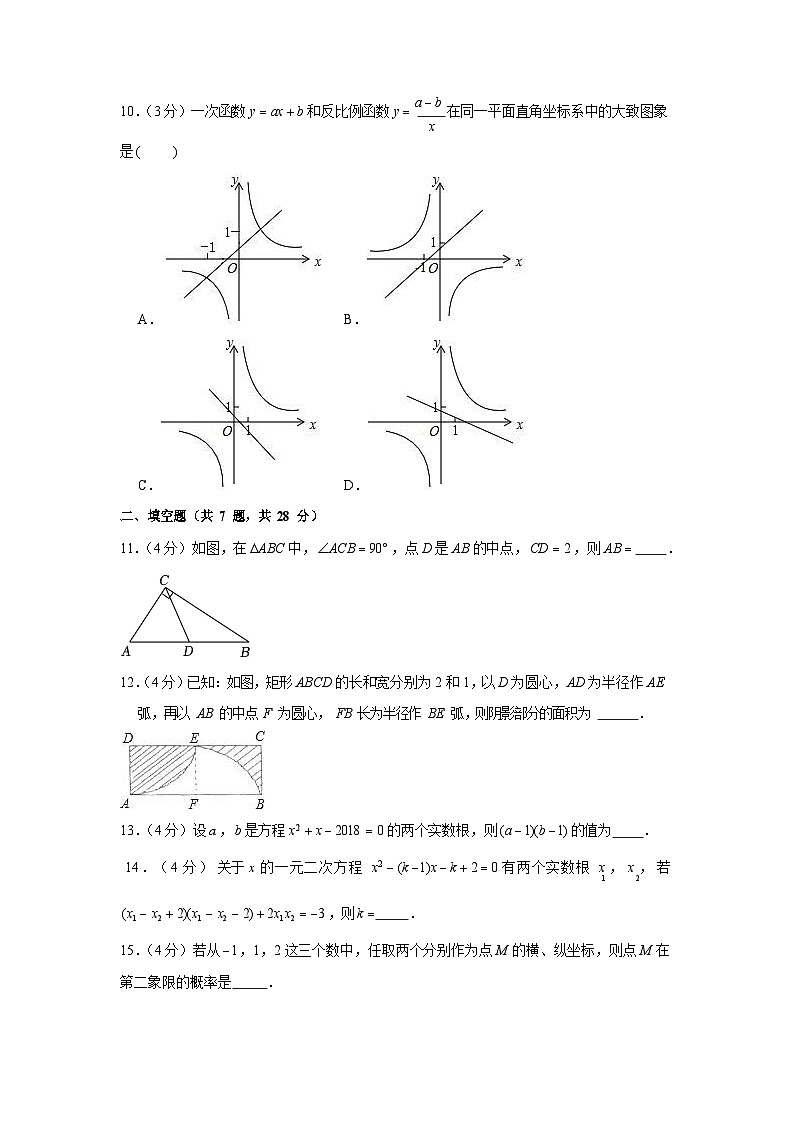
10.(3 分)一次函数 y ax b 和反比例函数 y a b 在同一平面直角坐标系中的大致图象
x
是()
A. B.
C. D.
二、填空题(共 7 题,共 28 分)
11.(4 分)如图,在ABC 中, ACB 90 ,点 D 是 AB 的中点, CD 2 ,则 AB .
12.(4 分)已知:如图,矩形 ABCD 的长和宽分别为 2 和 1,以 D 为圆心,AD 为半径作 AE
弧,再以 AB 的中点 F 为圆心, FB 长为半径作 BE 弧,则阴影部分的面积为.
13.(4 分)设 a , b 是方程 x2 x 2018 0 的两个实数根,则(a 1)(b 1) 的值为 .
14 .( 4 分) 关于 x 的一元二次方程 x2 (k 1)x k 2 0 有两个实数根 x , x , 若
12
(x1 x2 2)(x1 x2 2) 2x1 x2 3 ,则 k .
15.(4 分)若从1 ,1,2 这三个数中,任取两个分别作为点 M 的横、纵坐标,则点 M 在第二象限的概率是.
16.(4 分)如图,在矩形 ABCD 中, AB 1 , BC 2 , P 为线段 BC 上的一动点,且和 B 、 C 不重合,连接 PA ,过点 P 作 PE PA 交CD 于 E ,将 PEC 沿 PE 翻折到平面内,使点C 恰好落在 AD 边上的点 F ,则 BP 长为.
17.(4 分)如图,函数 y x 与 y 4 的图象相交于 A 、 B 两点,过 A 、 B 两点分别作 x 轴
x
垂线,垂足分别为点C 、 D ,则四边形 ACBD 的面积为.
三、解答题(共 8 题,共 62 分)
18.(6 分)先观察如图的立体图形,再分别画出从它的正面、左面、上面三个方向所看到的平面图形.
19.(6 分)已知关于 x 的方程 x2 2mx m2 4m 1 0
若这个方程有实数根,求 m 的取值范围;
若此方程有一个根是 1,请求出 m 的值.
20.(6 分)将 A , B , C , D 四人随机分成甲、乙两组参加羽毛球比赛,每组两人.
A 在甲组的概率是多少?
A , B 都在甲组的概率是多少?
21.(8 分)如图,点 D , E 在线段 BC 上, ADE 是等边三角形,且BAC 120
求证: ABD∽CAE ;
若 BD 2 , CE 8 ,求 BC 的长.
22.(8 分)如图,在平行四边形 ABCD 中, AB 3 , BC 5 .
尺规作图:作ABC 的平分线 BF ,分别与 AC 、 AD 交于点 E 、 F .
求 AE 的值.
EC
23.(8 分)如图,一棵大树在一次强台风中折断倒下,未折断树杆 AB 与地面仍保持垂直的关系,而折断部分 AC 与未折断树杆 AB 形成53 的夹角.树杆 AB 旁有一座与地面垂直的铁塔 DE ,测得 BE 6 米,塔高 DE 9 米.在某一时刻的太阳照射下,未折断树杆 AB 落在地面的影子 FB 长为 4 米,且点 F 、 B 、C 、 E 在同一条直线上,点 F 、 A 、 D 也在同一条直线上.求这棵大树没有折断前的高度.(参考数据:sin 53 0.8 ,cs 53 0.6 , tan 53 1.33)
24.(10 分)如图 1,在平面直角坐标系中, OABC 的一个顶点与坐标原点重合, OA 边落
在 x 轴上,且OA 4 , OC 2
, COA 45 .反比例函数 y k (k 0, x 0) 的图象
2
x
经过点C ,与 AB 交于点 D ,连接 AC , CD .
试求反比例函数的解析式;
求证: CD 平分ACB ;
如图 2,连接OD ,在反比例函数图象上是否存在一点 P ,使得 S
存在,请直接写出点 P 的坐标.如果不存在,请说明理由.
POC
1 S
2
COD
?如果
25.(10 分)如图 1,在ABC 中,点 D 、 E 分别在 AB 、 AC 上, DE / / BC , AD AE ,
(1)求证: B C ;
若BAC 90 ,把 ADE 绕点 A 逆时针旋转到图 2 的位置,点 M ,P ,N 分别为 DE ,
DC , BC 的中点,连接 MN , PM , PN .
①判断PMN 的形状,并说明理由;
②把ADE 绕点 A 在平面内自由旋转,若 AD 4 , AB 10 ,试问PMN 面积是否存在最大值;若存在,求出其最大值.若不存在,请说明理由.
2022-2023 学年广东省广州市荔湾区真光中学九年级(上)期末数学试卷
参考答案与试题解析
一、选择题(共 10 题,共 30 分)
1.(3 分)一元二次方程3x2 x 2 0 的二次项系数是 3,它的一次项系数是()
1
2
D.0
【解答】解:一次项系数为1 , 故选: A .
2.(3 分)如图所示,将矩形纸片 ABCD 折叠,使点 D 与点 B 重合,点C 落在点C 处,折痕为 EF ,若ABE 20 ,那么EFC 的度数为()
A.115B.120C.125D.130
【解答】解: RtABE 中, ABE 20 ,
AEB 70 ;
由折叠的性质知: BEF DEF ; 而BED 180 AEB 110 ,
BEF 55 ;
易知EBC D BCF C 90 ,
BE / /CF ,
EFC 180 BEF 125 . 故选: C .
3.(3 分)一元二次方程 x2 2(3x 2) (x 1) 0 的一般形式是()
A. x2 5x 5 0
B. x2 5x 5 0
C. x2 5x 5 0
D. x2 5 0
【解答】解:一元二次方程 x2 2(3x 2) (x 1) 0 的一般形式是 x2 5x 5 0 .
故选: A .
4.(3 分)“凤鸣”文学社在学校举行的图书共享仪式上互赠图书,每个同学都把自己的图书向本组其他成员赠送一本,某组共互赠了 210 本图书,如果设该组共有 x 名同学,那么依题意,可列出的方程是( )
A. x(x 1) 210
B. x(x 1) 210
C. 2x(x 1) 210
D. 1 x(x 1) 210
2
【解答】解:由题意得, x(x 1) 210 , 故选: B .
5.(3 分)在一个不透明的布袋中,红色、黑色、白色的玻璃球共有 40 个,除颜色外其他
完全相同,小明通过多次摸球试验后发现其中摸到红色球、黑色球的频率稳定在15% 和
45% ,则口袋中白色球的个数可能是()
A.24B.18C.16D.6
【解答】解:摸到红色球、黑色球的频率稳定在15% 和 45% ,
摸到白球的频率为1 15% 45% 40% ,
故口袋中白色球的个数可能是 40 40% 16 个. 故选: C .
6.(3 分)路边有一根电线杆 AB 和一块长方形广告牌,有一天小明突然发现在太阳光照射下,电线杆顶端 A 的影子刚好落在长方形广告牌的上边中点G 处,而长方形广告牌的影子刚好落在地面上 E 点(如图),已知 BC 5 米,长方形广告牌的长 HF 4 米,高 HC 3 米, DE 4 米,则电线杆 AB 的高度是()
A.6.75 米B.7.75 米C.8.25 米D.10.75 米
【解答】解:过点G 作GQ BE 于点Q , GP AB 于点 P ,
根据题意,四边形 BQGP 是矩形,
BP GQ 3 米,
APG∽FDE ,
AP 5 2 ,
34
AP 21 ,
4
AB 21 3 8.25 (米) ,
4
故选: C .
7.(3 分)如图,在正方形 ABCD 中,点 E 为 AB 边的中点,点 F 在 DE 上, CF CD ,过点 F 作 FG FC 交 AD 于点 G .下列结论:① GF GD ;② AG AE ;③ AF DE ;④ DF 4EF .正确的是( )
A.①②B.①③C.①③④D.③④
【解答】解:连接CG 交 ED 于点 H .如图所示:
四边形 ABCD 是正方形,
ADC 90 ,
FG FC ,
GFC 90 ,
在RtCFG 与RtCDG 中, CG CG ,
CF CD
RtCFG RtCDG(HL) ,
GF GD ,①正确.
CF CD , GF GD ,
点G 、C 在线段 FD 的中垂线上,
FH HD , GC DE ,
EDC DCH 90 ,
ADE EDC 90 ,
ADE DCH ,
四边形 ABCD 是正方形,
AD DC AB , DAE CDG 90 ,
EAD GDC
在ADE 和DCG 中, AD DC,
ADE DCH
ADE DCG (ASA) ,
AE DG ,
点 E 是边 AB 的中点,
点G 是边 AD 的中点,
AE AG ,②不正确;
点 H 是边 FD 的中点,
GH 是AFD 的中位线,
GH / / AF ,
AFD GHD ,
GH FD ,
GHD 90 ,
AFD 90 ,
即 AF DE ,③正确;
AD AB , AB 2AE ,
AD 2 AE ,
AFE 90 DAE , AEF DEA ,
ADE∽FAE ,
DE AD AE 2 ,
AEAFEF
DE 2AE , AE 2EF ,
DF 4EF ,④正确; 故选: C .
8.(3 分)设 x , x 是一元二次方程 x2 2x 3 0 的两根,则 x2 x2 ()
1212
A.2B. 2
C. 1
D.10
【解答】解:根据根与系数的关系可得 x1 x2 2 , x1 x2 3 ,
12121 2
所以 x2 x2 (x x )2 2x x 4 2 (3) 10 .
故选: D .
9.(3 分)若关于 x 的方程 x2 2x m 1 0 有两个实根 x 、 x ,则 x x (x2 x2 ) 2x2 4x
121 2 1211
【解答】解:关于 x 的方程 x2 2x m 1 0 有两个实根 x 、 x ,
12
△ 4 4(m 1) 8 4m0 ,
m2 ,
的最大值是(
)
A.3
B.4
C.4.5
D.5
x x 2 , x x m 1 , x2 2x
m 1 ,
121211
12121 2
x2 x2 (x x )2 2x x 4 2(m 1) 6 2m ,
x x (x2 x2 ) 2x2 4x
m2 ,
(m 1)(6 2m) 2(m 1) 2m2 10m 8 2(m 5 )2 9 ,
1 2 1211
22
1 2 1211
当 m 2 时, x x (x2 x2 ) 2x2 4x 的最大值 4 ,
故选: B .
10.(3 分)一次函数 y ax b 和反比例函数 y a b 在同一平面直角坐标系中的大致图象
x
是()
A.
B. C. D.
【解答】解:图 A 、 B 直线 y ax b 经过第一、二、三象限,
a 0 、b 0 ,
y 0 时, x b ,即直线 y ax b 与 x 轴的交点为( b , 0)
aa
由图 A 、 B 的直线和 x 轴的交点知: b 1 ,
a
即b a , 所以b a 0
a b 0 ,
此时双曲线在第一、三象限.
故选项 B 不成立,选项 A 正确.
图C 、 D 直线 y ax b 经过第二、一、四象限,
a 0 , b 0 ,
此时 a b 0 ,双曲线位于第二、四象限, 故选项C 、 D 均不成立;
故选: A .
二、填空题(共 7 题,共 28 分)
11.(4 分)如图,在ABC 中, ACB 90 ,点 D 是 AB 的中点,CD 2 ,则 AB 4.
【解答】解:ACB 90 , D 为 AB 中点,
CD 1 AB ,
2
AB 2CD ,
CD 2 ,
AB 2CD 4 . 故答案为:4.
12.(4 分)已知:如图,矩形 ABCD 的长和宽分别为 2 和 1,以 D 为圆心,AD 为半径作 AE
弧,再以 AB 的中点 F 为圆心, FB 长为半径作 BE 弧,则阴影部分的面积为 1.
【解答】解: AF BF , AD 1 , AB 2 ,
AD BF 1 ,
扇形 DAE 的面积 扇形 FBE 的面积,
阴影部分的面积 11 1. 故答案为 1.
13.(4 分)设 a ,b 是方程 x2 x 2018 0 的两个实数根,则(a 1)(b 1) 的值为 2016 .
【解答】解:
a , b 是方程 x2 x 2018 0 的两个实数根,
a b 1 , ab 2018 ,
(a 1)(b 1) ab a b 1 ab (a b) 1 2018 (1) 1 2016 , 故答案为: 2016 .
14 .( 4 分) 关于 x 的一元二次方程 x2 (k 1)x k 2 0 有两个实数根 x , x , 若
12
(x1 x2 2)(x1 x2 2) 2x1 x2 3 ,则 k 2.
【解答】解:关于 x 的一元二次方程 x2 (k 1)x k 2 0 的两个实数根为 x , x ,
12
x1 x2 k 1 , x1 x2 k 2 .
(x x 2)(x x 2) 2x x 3 ,即(x x )2 2x x
4 3 ,
12121 2121 2
(k 1)2 2k 4 4 3 , 解得: k 2 .
关于 x 的一元二次方程 x2 (k 1)x k 2 0 有实数根,
△ [(k 1)]2 4 1 (k 2)0 ,
2
解得: k2
1或 k 2
1 ,
2
k 2 .
故答案为:2.
15.(4 分)若从1 ,1,2 这三个数中,任取两个分别作为点 M 的横、纵坐标,则点 M 在
第二象限的概率是1.
3
【解答】解:列表如下:
由表可知,共有 6 种等可能结果,其中点 M 在第二象限的有 2 种结果,
所以点 M 在第二象限的概率是 2 1 ,
63
故答案为: 1 .
3
16.(4 分)如图,在矩形 ABCD 中, AB 1 , BC 2 , P 为线段 BC 上的一动点,且和 B 、
C 不重合,连接 PA ,过点 P 作 PE PA 交CD 于 E ,将 PEC 沿 PE 翻折到平面内,使点C
恰好落在 AD 边上的点 F ,则 BP 长为1 或 1.
3
【解答】解:作 PH AD 于 H ,如图,设 BP x ,则CP 2 x .
PE PA ,
2 3 90 ,
1 2 90 ,
1 3 ,
RtABP∽RtPCE ,
AB BP .即 1
x .
PCCE
2 xCE
CE x(2 x) .
PEC 沿 PE 翻折到PEF 位置,使点 F 落到 AD 上,
EF CE x(2 x) , PF PC 2 x , PFE C 90 ,
DE DC CE 1 x(2 x) (x 1)2 .
5 6 90 .
4 6 90 ,
5 4 .
RtPHF∽RtFDE ,
PH PF ,即 1 2 x .
FDFE
FD x ,
在RtDFE 中,
FDx(2 x)
DE2 DF 2 FE2 ,
[(x 1)2 ]2 x2 [x(2 x)]2 ,
解得 x 1 , x 1 ,
132
1
BP 的长为
或 1.
3
解法二:过点 A 作 AM BF 于 M .
PEF 由PEC 翻折得到,
PEF PEC ,
PF PC , FPE EPC ,
又BPA EPC 90 , APM EPF 90 ,
APB APM ,
又B AMP 90 , AP AP ,
ABP AMP (AAS ) ,
AB AM 1, BP PM ,
令 BP x ,则 PC PF 2 x , BP PM x ,
MF 2 x x 2 2x ,
AD / / BC ,
APB PAD ,
又APB APF ,
APF 为等腰三角形,
AF PF 2 x ,
在AMF 中, AF 2 AM 2 MF 2 ,
(2 x)2 12 (2 2x)2 ,
x 1 或 1 .
3
1
故答案为:
或 1.
3
17.(4 分)如图,函数 y x 与 y 4 的图象相交于 A 、 B 两点,过 A 、 B 两点分别作 x 轴
x
垂线,垂足分别为点C 、 D ,则四边形 ACBD 的面积为 8.
【解答】解:设 A 的坐标是(m, n) ,则 B 的坐标是(m, n) , mn 4
则 AC n , CD 2m .
则四边形 ACBD 的面积 AC CD 2mn 8 . 故答案为:8.
三、解答题(共 8 题,共 62 分)
18.(6 分)先观察如图的立体图形,再分别画出从它的正面、左面、上面三个方向所看到的平面图形.
【解答】解:如图所示:
19.(6 分)已知关于 x 的方程 x2 2mx m2 4m 1 0
若这个方程有实数根,求 m 的取值范围;
若此方程有一个根是 1,请求出 m 的值.
【解答】解:(1)根据题意知△ (2m)2 4(m2 4m 1)0 ,
解得: m 1 ;
4
(2)将 x 1 代入方程得1 2m m2 4m 1 0 , 整理,得: m2 6m 0 ,
解得: m1 0 , m2 6 ,
m 1 ,
4
m 0 和 m 6 均符合题意, 故 m 0 或 m 6 .
20.(6 分)将 A , B , C , D 四人随机分成甲、乙两组参加羽毛球比赛,每组两人.
A 在甲组的概率是多少?
A , B 都在甲组的概率是多少?
【解答】解:所有可能出现的结果如下:
总共有 6 种结果,每种结果出现的可能性相同.
所有的结果中,满足 A 在甲组的结果有 3 种,所以 A 在甲组的概率是 1 .(2 分)
2
甲组
乙组
结果
AB
CD
( AB, CD)
AC
BD
( AC, BD)
AD
BC
( AD, BC)
BC
AD
(BC, AD)
BD
A C
(BD, AC)
CD
AB
(CD, AB)
所有的结果中,满足 A ,B 都在甲组的结果有 1 种,所以 A ,B 都在甲组的概率是 1 .(6
6
分)
21.(8 分)如图,点 D , E 在线段 BC 上, ADE 是等边三角形,且BAC 120
求证: ABD∽CAE ;
若 BD 2 , CE 8 ,求 BC 的长.
【解答】(1)证明: BAC 120 , DAE 60 ,
BAD EAC 60 ,
ADE 是等边三角形,
ADE AED 60 ,
BAD B 60 , ADB AEC 120 ,
B EAC ,又ADB AEC ,
ABD∽CAE ;
(2)解: ABD∽CAE ,
BD AD ,即 AD2 BDCE 16 ,
AECE
解得, AD 4 ,则 DE 4 ,
BC BD DE EC 14 .
22.(8 分)如图,在平行四边形 ABCD 中, AB 3 , BC 5 .
尺规作图:作ABC 的平分线 BF ,分别与 AC 、 AD 交于点 E 、 F .
求 AE 的值.
EC
【解答】(1)解:如图所示:
(2)证明: ABCD 中 AD / / BC ,
AFB FBC ,
又ABF FBC ,
ABF AFB ,
AB AF ,
AFE CBE , AEF CEB ,
AEF∽CEB ,
当 AB 3 , BC 5 时,
AF 3 ,
AE AF 3 .
ECBC5
23.(8 分)如图,一棵大树在一次强台风中折断倒下,未折断树杆 AB 与地面仍保持垂直的关系,而折断部分 AC 与未折断树杆 AB 形成53 的夹角.树杆 AB 旁有一座与地面垂直的铁塔 DE ,测得 BE 6 米,塔高 DE 9 米.在某一时刻的太阳照射下,未折断树杆 AB 落在地面的影子 FB 长为 4 米,且点 F 、 B 、C 、 E 在同一条直线上,点 F 、 A 、 D 也在同一条直线上.求这棵大树没有折断前的高度.(参考数据:sin 53 0.8 ,cs 53 0.6 , tan 53 1.33)
【解答】解: AB EF , DE EF ,
ABC 90 , AB / / DE ,
FAB∽FDE ,
AB FB ,
DEFE
FB 4 米, BE 6 米, DE 9 米,
AB
4,得 AB 3.6 米,
94 6
ABC 90 , BAC 53 , csBAC AB ,
AC
AC
AB
csBAC
3.6 6 米,
0.6
AB AC 3.6 6 9.6 米,
即这棵大树没有折断前的高度是 9.6 米.
24.(10 分)如图 1,在平面直角坐标系中, OABC 的一个顶点与坐标原点重合, OA 边落
在 x 轴上,且OA 4 , OC 2
, COA 45 .反比例函数 y k (k 0, x 0) 的图象
2
x
经过点C ,与 AB 交于点 D ,连接 AC , CD .
试求反比例函数的解析式;
求证: CD 平分ACB ;
如图 2,连接OD ,在反比例函数图象上是否存在一点 P ,使得 S
存在,请直接写出点 P 的坐标.如果不存在,请说明理由.
【解答】解:(1)如图 1,过点C 作CE x 轴于 E ,
CEO 90 ,
COA 45 ,
OCE 45 ,
POC
1 S
2
COD
?如果
2
OC 2,
OE CE 2 ,
C(2, 2) ,
点C 在反比例函数图象上,
k 2 2 4 ,
反比例函数解析式为 y 4 ,
x
(2)如图 2,过点 D 作 DG x 轴于G ,交 BC 于 F ,
CB / / x 轴,
GF CB ,
OA 4 ,
由(1)知, OE CE 2 ,
AE EC 2 ,
ECA 45 , OCA 90 ,
OC / / AB ,
BAC OCA 90 ,
AD AC ,
A(4, 0) , AB / /OC ,
直线 AB 的解析式为 y x 4 ①,
反比例函数解析式为 y 4 ②,
x
2
联立①②解得, x 2
2x 2 2
2
或
(舍) ,
2
2
2
y 2 2 y 2 2
2
D(2
2 , 2
2) ,
2
AG DG 2 2 ,
2
AD 2DG 4 2,
2
DF 2 (2 2 2) 4 2,
AD DF ,
AD AC , DF CB ,
点 D 是ACB 的角平分线上, 即: CD 平分ACB ;
(3)存在,点C(2, 2) ,
2
2
直线OC 的解析式为 y x , OC 2,
2
D(2
2 , 2
2) ,
2
CD 2 2
Ⅰ、如图 3,当点 P 在点C 右侧时,即:点 P 的横坐标大于 2,
SPOC
1 S
2
COD ,
设CD 的中点为 M ,
2
M ( 2 , 2) ,
过点 M 作 MP / /OC 交双曲线于 P ,
直线 PM 的解析式为 y x 2 ③,
反比例函数解析式为 y 4 ④,
x
联立③④解得,
5
5
x 1 或 x 1
5
(舍) ,
5
y 1
y 1
5
P(
1 ,
1) ;
5
Ⅱ、当点 P 在点C 左侧时,即:点 P 的横坐标大于 0 而小于 2, 设点 M 关于OC 的对称点为 M , M (m, n) ,
m
2 2 2 , n
2 2 ,
22
2
2
m 2 , n 4 ,
2
M (2 , 4
2) ,
PM / /OC ,
直线 PM 的解析式为 y x 2 ⑤,
5
联立④⑤解得, x 1 或x 1
5
(舍) ,
5
5
5
y 1
y 1
5
5
5
5
P(
1 ,
1) .
5
即:点 P 的坐标为(
1 ,
1) 或 P(
1 ,
1) .
25.(10 分)如图 1,在ABC 中,点 D 、 E 分别在 AB 、 AC 上, DE / / BC , AD AE ,
(1)求证: B C ;
(2)若BAC 90 ,把 ADE 绕点 A 逆时针旋转到图 2 的位置,点 M ,P ,N 分别为 DE ,
DC , BC 的中点,连接 MN , PM , PN .
①判断PMN 的形状,并说明理由;
②把ADE 绕点 A 在平面内自由旋转,若 AD 4 , AB 10 ,试问PMN 面积是否存在最大值;若存在,求出其最大值.若不存在,请说明理由.
【解答】解:(1) AD AE ,
ADE AED ,
DE / / BC ,
ADE B , AED C ,
B C .
(2)① PMN 是等腰直角三角形,
理由:点 P , M 分别是CD , DE 的中点,
PM 1 CE , PM / /CE ,
2
点 N , M 分别是 BC , DE 的中点,
PN 1 BD , PN / / BD ,
2
BD CE ,
PM PN ,
PMN 是等腰三角形,
PM / /CE ,
DPM DCE ,
PN / / BD ,
PNC DBC ,
DPN DCB PNC DCB DBC ,
MPN DPM DPN
DCE DCB DBC
BCE DBC
ACB ACE DBC
ACB ABD DBC
ACB ABC ,
BAC 90 ,
ACB ABC 90 ,
MPN 90 ,
PMN 是等腰直角三角形,
②由①知, PMN 是等腰直角三角形, PM PN 1 BD ,
2
PM 最大时, PMN 面积最大,
点 D 在 AB 的延长线上,
BD AB AD 14 ,
PM 7 ,
SPMN最大
1 PM 2 1 72 49 .
222
故答案为 49
2
相关试卷
这是一份2022-2023学年广东省广州市荔湾区九年级(上)期末数学试卷(含答案),共32页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份2022-2023学年广东省广州市荔湾区广雅中学九年级(上)期末数学试卷2(含答案),共24页。试卷主要包含了填空题,解答题等内容,欢迎下载使用。
这是一份广东省广州市荔湾区真光中学2024-—2025学年 上学期9月月考九年级数学试卷,共8页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。









