2022-2023学年广东省广州市天河区华南师大附中九年级（上）期末数学试卷（含答案）

这是一份2022-2023学年广东省广州市天河区华南师大附中九年级（上）期末数学试卷（含答案），共32页。试卷主要包含了填空题，解答题等内容，欢迎下载使用。

有一个是正确的）
1．（3 分）下列图形中，既是轴对称图形，又是中心对称图形的是()
A． B． C． D．
2．（3 分）如图，一个游戏转盘中，红、黄、蓝三个扇形的圆心角度数分别为60 ，90 ，210 ．让转盘自由转动，指针停止后落在黄色区域的概率是()
1
6
1
4
1
3
7
12
3．（3 分）将二次函数 y  x2 图象向左平移 1 个单位，再向下平移 2 个单位后，所得图象的函数是()
A． y  (x  1)2  2
B． y  (x 1)2  2
C． y  (x  1)2  2
D． y  (x 1)2  2
4．（3 分）如图， AB 是O 的直径， CD 为弦， CD  AB 于点 E ，则下列结论中不成立的是()
AC  AD
BC  BD
OE  BE
CE  DE
5．（3 分）已知关于 x 的一元二次方程 x2  2x  m  0 有两个不相等的实数根，则()
m  1
m  1
m  0
D． 0  m  1
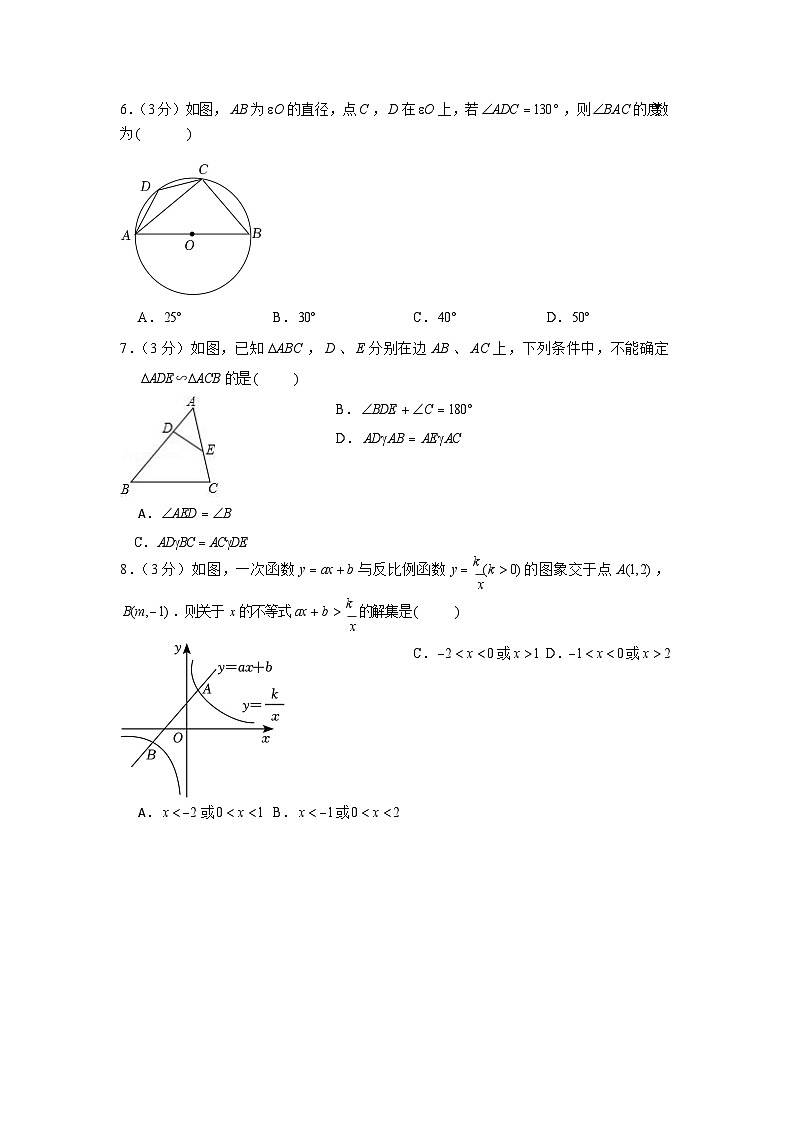
6．（3 分）如图， AB 为O 的直径，点C ， D 在O 上，若ADC  130 ，则BAC 的度数为()
A． 25B． 30C． 40D． 50
7．（3 分）如图，已知 ABC ， D 、 E 分别在边 AB 、 AC 上，下列条件中，不能确定
ADE∽ACB 的是()
A． AED  B
C． ADBC  ACDE
B． BDE  C  180
D． AD AB  AE AC
8．（3 分）如图，一次函数 y  ax  b 与反比例函数 y  k (k  0) 的图象交于点 A(1, 2) ，
x
B(m, 1) ．则关于 x 的不等式 ax  b  k 的解集是()
x
A． x  2 或0  x  1
B． x  1 或0  x  2
C． 2  x  0 或 x  1 D．1  x  0 或 x  2
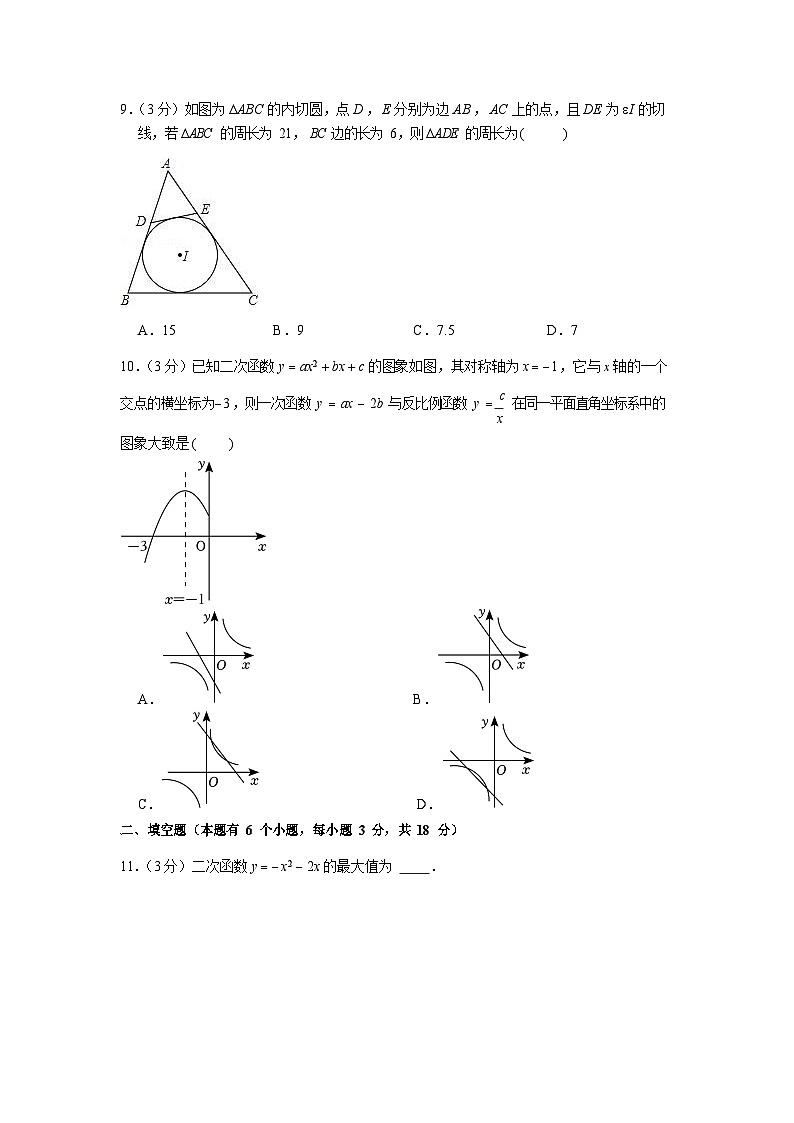
9．（3 分）如图为ABC 的内切圆，点 D ， E 分别为边 AB ， AC 上的点，且 DE 为I 的切线，若ABC 的周长为 21， BC 边的长为 6，则ADE 的周长为()
A．15B．9C．7.5D．7
10．（3 分）已知二次函数 y  ax2  bx  c 的图象如图，其对称轴为 x  1 ，它与 x 轴的一个
交点的横坐标为3 ，则一次函数 y  ax  2b 与反比例函数 y  c 在同一平面直角坐标系中的
x
图象大致是()
A．
B．
C． D．
二、填空题（本题有 6 个小题，每小题 3 分，共 18 分）
11．（3 分）二次函数 y  x2  2x 的最大值为 ．
12．（3 分）如图，乐器上的一根弦 AB 的长度为30cm ，两个端点 A 、B 固定在乐器板面上，支撑点C 是弦 AB 靠近点 B 的黄金分割点，则线段 AC 的长度为 cm ．（结果保留根号，
参考数据：黄金分割数： 5  1)
2
13．（3 分）如图，点 A 是反比例函数 y  2 (x  0) 的图象上任意一点， AB / / x 轴交反比例函
x
数 y   3 的图象于点 B ，以 AB 为边作平行四边形 ABCD ，其中C 、D 在 x 轴上，则 S
x
为．
ABCD
14．（3 分）如图放置的一个圆锥，它的主视图是直角边长为 2 的等腰直角三角形，则该圆锥侧面展开扇形的弧长为 ．（结果保留)
15．（3 分）如图，BE 是ABC 的中线，点 F 在 BE 上，延长 AF 交 BC 于点 D ．若 BF  3FE ，则 BD ．
DC
16．（3 分）如图，四边形 ABCD 、CEFG 都是正方形，点G 在线段CD 上，连接 BG 、DE ，
DE 和 FG 相交于点 O ， 设 AB  a ， CG  b(a  b) ． 下列结论： ① BCG  DCE ； ②
BG  DE ；③ DG  GO ；④ (a  b)2  S
GCCE
EFO
 b2  S
DGO
．其中结论正确的是．
三、解答题（本题有 9 小题，共 72 分，解答要求写出文字说明，证明过程或计算步骤）
17．（4 分）如图，若ADE  B ， BAD  CAE ．求证： ADE∽ABC ．
18．（4 分）如图， AB 是O 的直径， AC 的中点 D 在O 上， DE  BC 于 E ．求证： DE是O 的切线．
19．（6 分）先化简，再求值： (m  4m  4)  m  2 ，其中 m 是方程 2x2  4x 1  0 的根．
mm2
20．（6 分）已知一艘轮船上装有 100 吨货物，轮船到达目的地后开始卸货．设平均卸货速度为 v （单位：吨/ 小时），卸完这批货物所需的时间为t （单位：小时）．
求v 关于t 的函数表达式．
若要求不超过 5 小时卸完船上的这批货物，那么平均每小时至少要卸货多少吨？
21．（8 分）在平面直角坐标系中，ABC 的三个顶点坐标分别为 A(2, 4) ，B(3, 2) ，C(6, 3) ．
画出ABC 关于 x 轴对称的△ A1 B1C1 ；
以 M 点为位似中心，在网格中画出△ A1 B1C1 的位似图形△ A2 B2C2 ，使△ A2 B2C2 与△
A1B1C1 的相似比为2 :1 ．
22．（10 分）为了弘扬我国古代数学发展的伟大成就，某校九年级进行了一次数学知识竞赛，并设立了以我国古代数学家名字命名的四个奖项：“祖冲之奖”、“刘徽奖”、“赵爽奖”、“秦九韶奖”．根据获奖情况绘制了如图所示的条形统计图和扇形统计图．
获最高奖项“祖冲之奖”的学生成绩统计表：
根据图形信息，解答下列问题：
获得“秦九韶奖”的学生有多少人，并补全条形统计图；
获得“祖冲之奖”的学生成绩的中位数是分，众数是分；
若从获得“祖冲之奖”且得分为 95 分的甲，乙，丙，丁四名同学中随机抽取 2 名参加市级数学知识竞赛，请用列表法或画树状图的方法，求出恰好抽到甲和乙的概率．
分数/ 分
80
85
90
95
人数/ 人
4
2
10
4
23．（10 分）如图，在平面直角坐标系中，菱形 ABCD 的顶点 D 在 y 轴上， A ，C 两点的坐
标分别为(4, 0) ，(4, m) ，直线CD : y  ax  b(a  0) 与反比例函数 y  k (k  0) 的图象交于C ，
x
P(8, 2) 两点．
求该反比例函数的解析式及 m 的值；
判断点 B 是否在该反比例函数的图象上，并说明理由．
24．（12 分）如图，抛物线 y   1 x2  3 x  2 与 x 轴交于 A 、B 两点（点 A 在点 B 的左边），
22
与 y 轴交于点C ，连接 BC ．
求点 A 、 B 、C 的坐标；
设 x 轴上的一个动点 P 的横坐标为t ，过点 P 作直线 PN  x 轴，交抛物线于点 N ，交直线 BC 于点 M ．
①当点 P 在线段 AB 上时，设 MN 的长度为 s ，求 s 与t 的函数关系式；
②当点 P 在线段OB 上时，是否存在点 P ，使得以O 、P 、N 三点为顶点的三角形与COB
相似？若存在，请求出点 P 的坐标；若不存在，请说明理由．
25．（12 分）如图①，已知O 是ABC 的外接圆，ABC  ACB  (45   90 ， D 为
AB 上一点，连接CD 交 AB 于点 E ．
连接 BD ，若CDB  40 ，求的大小；
如图②，若点 B 恰好是CD 中点，求证： CE 2  BE  BA ；
如图③，将CD 分别沿 BC 、 AC 翻折得到CM 、CN ，连接 MN ，若CD 为直径，请问 AB 是否为定值，如果是，请求出这个值，如果不是，请说明理由．
MN
2022-2023 学年广东省广州市天河区华南师大附中九年级（上） 期末数学试卷
参考答案与试题解析
一、选择题（本题有 10 个小题，每小题 3 分，满分 30 分，每小题给出的四个选项中，只有一个是正确的）
1．（3 分）下列图形中，既是轴对称图形，又是中心对称图形的是()
A． B． C． D．
【解答】解： A ．该图形既不是中心对称图形，也不是轴对称图形，故此选项不合题意；
B ．该图形既是轴对称图形，又是中心对称图形，故此选项符合题意； C ．该图形不是中心对称图形，是轴对称图形，故此选项不合题意； D ．该图形是轴对称图形，不是中心对称图形，故此选项不合题意． 故选： B ．
2．（3 分）如图，一个游戏转盘中，红、黄、蓝三个扇形的圆心角度数分别为60 ，90 ，210 ．让转盘自由转动，指针停止后落在黄色区域的概率是()
1
6
1
4
1
3
7
12
【解答】解：黄扇形区域的圆心角为90 ，
所以黄区域所占的面积比例为 90  1 ，
3604
即转动圆盘一次，指针停在黄区域的概率是 1 ，
4
故选： B ．
3．（3 分）将二次函数 y  x2 图象向左平移 1 个单位，再向下平移 2 个单位后，所得图象的函数是()
A． y  (x  1)2  2
B． y  (x 1)2  2
C． y  (x  1)2  2
D． y  (x 1)2  2
【解答】解：原抛物线的顶点为(0, 0) ，向左平移 1 个单位，再向下平移 2 个单位，那么新
抛物线的顶点为(1, 2) ，
可设新抛物线的解析式为： y  (x  h)2  k ， 代入得： y  (x  1)2  2 ．
所得图象的解析式为： y  (x  1)2  2 ；
故选： C ．
4．（3 分）如图， AB 是O 的直径， CD 为弦， CD  AB 于点 E ，则下列结论中不成立的是()
AC  AD
BC  BD
OE  BE
CE  DE
【解答】解：如图， AB 是O 的直径， CD 是弦， CD  AB 于点 E ，
弧 BD  弧 BC ，弧 AC  弧 AD ， CE  DE ，
选项 A 、 B 、 D 正确，不符合题意；
OE 和 BE 的大小关系不能证明，故选项C 符合题意； 故选： C ．
5．（3 分）已知关于 x 的一元二次方程 x2  2x  m  0 有两个不相等的实数根，则()
m  1
m  1
m  0
D． 0  m  1
【解答】解：根据题意得△  (2)2  4m  0 ，
解得 m  1． 故选： A ．
6．（3 分）如图， AB 为O 的直径，点C ， D 在O 上，若ADC  130 ，则BAC 的度
数为()
A． 25B． 30C． 40D． 50
【解答】解：四边形 ABCD 是圆内接四边形，
ADC  B  180 ，
ADC  130 ，
B  180  130  50 ，
 AB 是O 的直径，
ACB  90 ，
BAC  90  B  40 ． 故选： C ．
7．（3 分）如图，已知 ABC ， D 、 E 分别在边 AB 、 AC 上，下列条件中，不能确定
ADE∽ACB 的是()
AED  B
BDE  C  180C．ADBC  ACDE
D． AD AB  AE AC
【解答】解： A 、由AED  B ， A  A ，则可判断ADE∽ACB ；
B 、由BDE  C  180 ， ADE  BDE  180 ，得ADE  C ， A  A ，则可判断
ADE∽ACB ；
C 、由 ADBC  ACDE ，得 AD  DE 不能判断ADE∽ACB ；
ACBC
D 、由 AD AB  AE AC 得 AD  AE ， A  A ，故能确定ADE∽ACB ，
ACAB
故选： C ．
8．（3 分）如图，一次函数 y  ax  b 与反比例函数 y  k (k  0) 的图象交于点 A(1, 2) ，
x
B(m, 1) ．则关于 x 的不等式 ax  b  k 的解集是()
x
A． x  2 或0  x  1 B． x  1 或0  x  2
【解答】解： A(1, 2) 在反比例函数图象上，
 k  1 2  2 ，
反比例函数解析式为 y  2 ，
x
 B(m, 1) 在反比例函数图象上，
C． 2  x  0 或 x  1 D．1  x  0 或 x  2
 m 
2  2 ，
1
 B(2, 1) ，
由题意得关于 x 的不等式 ax  b  k 的解集即为一次函数图象在反比例函数图象上方时自变
x
量的取值范围，
关于 x 的不等式 ax  b  k 的解集为2  x  0 或 x  1 ，
x
故选： C ．
9．（3 分）如图为ABC 的内切圆，点 D ， E 分别为边 AB ， AC 上的点，且 DE 为I 的切线，若ABC 的周长为 21， BC 边的长为 6，则ADE 的周长为()
A．15B．9C．7.5D．7
【解答】解：ABC 的周长为 21， BC  6 ，
 AC  AB  21  6  15 ，
设I 与ABC 的三边 AB 、 BC 、 AC 的切点为 M 、 N 、Q ，切 DE 为 P ，
 DM  DP ， BN  BM ， CN  CQ ， EQ  EP ，
 BM  CQ  BN  CN  BC  6 ，
ADE 的周长 AD  DE  AE  AD  AE  DP  PE
 AD  DM  AE  EQ
 AB  BM  AC  CQ
 AC  AB  (BM  CQ)
 15  6  9 ， 故选： B ．
10．（3 分）已知二次函数 y  ax2  bx  c 的图象如图，其对称轴为 x  1 ，它与 x 轴的一个交点的横坐标为3 ，则一次函数 y  ax  2b 与反比例函数 y  c 在同一平面直角坐标系中的
x
图象大致是()
A．
B．
C． D．
【解答】解：二次函数 y  ax2  bx  c 的图象开口向下，
 a  0 ，
其对称轴为 x  1 ，即 b
2a
 1，
b  2a ，
b  0 ，
图象与 y 轴的交点在 y 轴正半轴，
 c  0 ，
一次函数 y  ax  2b 的图象过一、二、四象限，
反比例函数 y  c 的图象过一、三象限，
x
由图象可知，二次函数 y  ax2  bx  c 的图象过点(3, 0) ，
 0  9a  3b  c ，
 b  2a ，
9a  6a  c  0 ，
 c  3a ，
令 c  ax  2b ，
x
 ax2  2bx  c  0 ， 即 ax2  4ax  3a  0 ，
△  (4a)2  4  a  3a  4a2  0 ，
一次函数 y  ax  2b 与反比例函数 y  c 有两个交点．
x
综上，一次函数 y  ax  2b 的图象过一、二、四象限，反比例函数 y  c 的图象过一、三象
x
限，且一次函数 y  ax  2b 与反比例函数 y  c 有两个交点．
x
故选： C ．
二、填空题（本题有 6 个小题，每小题 3 分，共 18 分）
11．（3 分）二次函数 y  x2  2x 的最大值为 1．
【解答】解： y  x2  2x  (x  1)2  1 ，
当 x  1 时， y 有最大值为 1．
故答案为：1．
12．（3 分）如图，乐器上的一根弦 AB 的长度为30cm ，两个端点 A 、B 固定在乐器板面上，
5
支撑点C 是弦 AB 靠近点 B 的黄金分割点，则线段 AC 的长度为(15
果保留根号，参考数据：黄金分割数： 5  1)
2
【解答】解：点C 是弦 AB 靠近点 B 的黄金分割点， AB  30cm ，
 15) cm ．（结
 AC 
5 1 AB 
5 1  30  (15 5  15)(cm ) ，
22
5
故答案为： (15
15) ．
13．（3 分）如图，点 A 是反比例函数 y  2 (x  0) 的图象上任意一点， AB / / x 轴交反比例函
x
数 y   3 的图象于点 B ，以 AB 为边作平行四边形 ABCD ，其中C 、D 在 x 轴上，则 S
x
为 5．
【解答】解：设点 A 的纵坐标为b ， 所以， 2  b ，
x
ABCD
解得 xA
 2 ，
b
 AB / / x 轴，
点 B 的纵坐标为 3  b ，
x
解得 xB
  3 ，
b
 AB  2  ( 3)  5 ，
bbb
 S ABCD
 5  b  5 ．
b
故答案为：5．
14．（3 分）如图放置的一个圆锥，它的主视图是直角边长为 2 的等腰直角三角形，则该圆锥侧面展开扇形的弧长为 2 2 ．（结果保留)
【解答】解：某圆锥的主视图是一个腰长为 2 的等腰直角三角形，
2
斜边长为 2，
则底面圆的周长为 2 2，
该圆锥侧面展开扇形的弧长为 2 2，
故答案为 2 2．
15．（3 分）如图，BE 是ABC 的中线，点 F 在 BE 上，延长 AF 交 BC 于点 D ．若 BF  3FE ，
则 BD 3．
DC2
【解答】解：如图， BE 是ABC 的中线，
点 E 是 AC 的中点，
 AE  1 ，
AC2
过点 E 作 EG / / DC 交 AD 于G ，
AGE  ADC ， AEG  C ，
AGE∽ADC ，
 GE  AE  1 ，
DCAC2
 DC  2GE ，
 BF  3FE ，
 EF  1 ，
BF3
GE / / BD ，
GEF  FBD ， EGF  BDF ，
GFE∽DFB ，
 GE  EF  1 ，
DBBF3
 DC  2 ，
DB3
 BD  3 ，
DC2
故答案为： 3 ．
2
16．（3 分）如图，四边形 ABCD 、CEFG 都是正方形，点G 在线段CD 上，连接 BG 、DE ，
DE 和 FG 相交于点 O ， 设 AB  a ， CG  b(a  b) ． 下列结论： ① BCG  DCE ； ②
BG  DE ；③ DG  GO ；④ (a  b)2  S
GCCE
EFO
 b2  S
DGO
．其中结论正确的是①②④ ．
【解答】解：①四边形 ABCD 和四边形CEFG 是正方形，
 BC  DC ， CG  CE ， BCD  ECG  90 ，
BCG  DCE ， 在BCG 和DCE 中，
BD  CD

BCG  DCE ，

CG  CE
BCG  DCE (SAS ) ， 故①正确；
②延长 BG 交 DE 于点 H ，
BCG  DCE ，
CBG  CDE ，
又CBG  BGC  90 ，
CDE  DGH  90 ，
DHG  90 ，
 BH  DE ；
 BG  DE ． 故②正确；
③ DC / / EF ，
GDO  OEF ，
GOD  FOE ，
OGD∽OFE ，
 SDGO  (
DG )2  (
a  b )2
(a  b)2

，
SEFOEF
bb2
EFODGO
(a  b)2  S b2  S． 故④正确；
故答案为：①②④．
三、解答题（本题有 9 小题，共 72 分，解答要求写出文字说明，证明过程或计算步骤）
17．（4 分）如图，若ADE  B ， BAD  CAE ．求证： ADE∽ABC ．
【解答】证明：BAD  CAE ，
BAD  BAE  BAE  CAE ，
DAE  BAC ，
ADE  B ，
ADE∽ABC ．
18．（4 分）如图， AB 是O 的直径， AC 的中点 D 在O 上， DE  BC 于 E ．求证： DE是O 的切线．
【解答】证明：连接OD ，
 AO  OB ， D 为 AC 的中点，
OD / / BC ，
 DE  BC ，
 DE  OD ，
 OD 是O 的半径，
 DE 是O 的切线．
19．（6 分）先化简，再求值： (m  4m  4)  m  2 ，其中 m 是方程2x2  4x 1  0 的根．
mm2
【解答】解：原式
m2  4m  4m2




(m  2)2m2


mm  2
mm  2
 m2  2m ．
 m 是方程2x2  4x 1  0 的根，
 2m2  4m  1  0 ．
 m2  2m  1 ，
2
原式 1 ．
2
20．（6 分）已知一艘轮船上装有 100 吨货物，轮船到达目的地后开始卸货．设平均卸货速度为 v （单位：吨/ 小时），卸完这批货物所需的时间为t （单位：小时）．
求v 关于t 的函数表达式．
若要求不超过 5 小时卸完船上的这批货物，那么平均每小时至少要卸货多少吨？
【解答】解：（1）由题意可得：100  vt ，
则v  100 (t  0) ；
t
（2）不超过 5 小时卸完船上的这批货物，
t5 ，
则v100  20 ，
5
答：平均每小时至少要卸货 20 吨．
21．（8 分）在平面直角坐标系中，ABC 的三个顶点坐标分别为 A(2, 4) ，B(3, 2) ，C(6, 3) ．
画出ABC 关于 x 轴对称的△ A1 B1C1 ；
以 M 点为位似中心，在网格中画出△ A1 B1C1 的位似图形△ A2 B2C2 ，使△ A2 B2C2 与△
A1B1C1 的相似比为2 :1 ．
【解答】解：（1）如图所示：△ A1 B1C1 ，即为所求；
（2）如图所示：△ A2 B2C2 ，即为所求．
22．（10 分）为了弘扬我国古代数学发展的伟大成就，某校九年级进行了一次数学知识竞赛，并设立了以我国古代数学家名字命名的四个奖项：“祖冲之奖”、“刘徽奖”、“赵爽奖”、“秦九韶奖”．根据获奖情况绘制了如图所示的条形统计图和扇形统计图．
获最高奖项“祖冲之奖”的学生成绩统计表：
根据图形信息，解答下列问题：
获得“秦九韶奖”的学生有多少人，并补全条形统计图；
获得“祖冲之奖”的学生成绩的中位数是 90分，众数是分；
若从获得“祖冲之奖”且得分为 95 分的甲，乙，丙，丁四名同学中随机抽取 2 名参加市级数学知识竞赛，请用列表法或画树状图的方法，求出恰好抽到甲和乙的概率．
【解答】解：（1）本次获奖人数有： 20 10%  200 （人) ，
则获得“秦九韶奖”的人数有 200  46%  92 （人) ．
则刘徽奖的人数为 200  (1  24%  46% 10%)  40 （人) ， 补全条形统计图如解图所示：
获得“祖冲之奖”的学生成绩的中位数是 90 分，众数是 90 分； 故答案为：90，90；
分数/ 分
80
85
90
95
人数/ 人
4
2
10
4
树状图如图所示，
从四人中随机抽取两人共有 12 种情况，并且每种情况出现的可能性相等，恰好是甲和乙
的有 2 种可能，分别是（甲，乙），（乙，甲）．
抽取两人恰好是甲和乙的概率是 2  1 ．
126
23．（10 分）如图，在平面直角坐标系中，菱形 ABCD 的顶点 D 在 y 轴上， A ，C 两点的坐
标分别为(4, 0) ，(4, m) ，直线CD : y  ax  b(a  0) 与反比例函数 y  k (k  0) 的图象交于C ，
x
P(8, 2) 两点．
求该反比例函数的解析式及 m 的值；
判断点 B 是否在该反比例函数的图象上，并说明理由．
【解答】解：（1）把 P(8, 2) 代入 y  k 得：
x
2  k ，
8
解得 k  16 ，
反比例函数的解析式为 y  16 ，
x
 C(4, m) 在反比例函数 y  16 的图象上，
x
 m  16  4 ；
4
反比例函数的解析式为 y  16 ， m  4 ；
x
（2） B 在反比例函数 y  16 的图象上，理由如下：
x
连接 AC ， BD 交于 H ，如图：
把C(4, 4) ， P(8, 2) 代入 y  ax  b 得：
4a  b  4

8a  b  2 ，

a  1
解得2 ，
b  2
直线CD 的解析式是 y  1 x  2 ，
2
在 y  1 x  2 中，令 x  0 得 y  2 ，
2
 D(0, 2) ，
四边形 ABCD 是菱形，
 H 是 AC 中点，也是 BD 中点， 由 A(4, 0) ， C(4, 4) 可得 H (4, 2) ，
设 B( p, q) ，
 D(0, 2) ，
 p  0  4
  2，

 q  2
 2
 2
q  2
解得 p  8 ，

 B(8, 2) ，
在 y  16 中，令 x  8 得 y  2 ，
x
 B 在反比例函数 y  16 的图象上．
x
24．（12 分）如图，抛物线 y   1 x2  3 x  2 与 x 轴交于 A 、B 两点（点 A 在点 B 的左边），
22
与 y 轴交于点C ，连接 BC ．
求点 A 、 B 、C 的坐标；
设 x 轴上的一个动点 P 的横坐标为t ，过点 P 作直线 PN  x 轴，交抛物线于点 N ，交直线 BC 于点 M ．
①当点 P 在线段 AB 上时，设 MN 的长度为 s ，求 s 与t 的函数关系式；
②当点 P 在线段OB 上时，是否存在点 P ，使得以O 、P 、N 三点为顶点的三角形与COB
相似？若存在，请求出点 P 的坐标；若不存在，请说明理由．
【解答】解：（1）点 A 、 B 、C 在二次函数图象上，
把 x  0 代入 y   1 x2  3 x  2 ，得 y  2 ，
22
把 y  0 代入 y   1 x2  3 x  2 ，得 x  1 ， x  4 ，
2212
 A(1, 0) ， B(4, 0) ， C(0, 2) ；
（2）①设直线 BC 的解析式为 y  kx  b(k  0) ，
b  2
把 B(4, 0) ， C(0, 2) 代入，得4k  b  0 ，


k   1
解得： 2 ，
b  2
直线 BC 的解析式为 y   1 x  2 ，
2
OP  t ，
 P(t, 0) ， M (t,  1 t  2) ， N (t,  1 t 2  3 t  2) ，如图：
222
 S  N P  M P   1 t 2  3 t  2  ( 1 t  2)   1 t 2  2t(0  t  4) ，
11 11 1
S2  M 2 P2  N2 P2
2222
  1 t  2  ( 1 t 2  3 t  2)  1 t 2  2t(1  t  0) ，
2222
 1 t 2  2t(1  t  0)
即 S   2；
1


 t 2  2t(0  t  4)
 2
②存在，理由： 如图：
若OPN∽COB ，当OP 与OC 是对应边时，则 OP  NP ，
COBO
即 1 t 
 1 t 2  3 t  2
22，
24
化简得： t 2  t  4  0 ，
解得： t  1 
2
17 （舍去负值），
若OPN∽BOC ，当OP 与OB 是对应边时，则 OP  PN ，
BOCO
即 t 
 1 t 2  3 t  2
22，
42
5
化简得： t 2  2t  4  0 ，
5
解得： t  1 ，（舍去负值），
符合题意的点 P 的坐标为( 1 
2
17 ， 0) 和(1 ， 0) ．
25．（12 分）如图①，已知O 是ABC 的外接圆，ABC  ACB  (45   90 ， D 为
AB 上一点，连接CD 交 AB 于点 E ．
连接 BD ，若CDB  40 ，求的大小；
如图②，若点 B 恰好是CD 中点，求证： CE 2  BE  BA ；
如图③，将CD 分别沿 BC 、 AC 翻折得到CM 、CN ，连接 MN ，若CD 为直径，请问 AB 是否为定值，如果是，请求出这个值，如果不是，请说明理由．
MN
【解答】解：（1） BC  BC ，
CAB  CDB  40 ，
ABC  ACB  CAB  180 ， ABC  ACB  ，
 1  (180  40)  70 ；
2
证明：点 B 是CD 的中点，
 BD  BC ，
DCB  A ，
ABC  CBE ，
BCE∽BAC ，
 BC  BE ，
BABC
 BC 2  BE  BA ，
ACB  ACD  BCD ， BEC  ACD  A ， BCD  A ，
ABC  ACB  BEC ，
 CB  CE ，
CE 2  BE  BA ；
是定值．
方法一：将CD 分别沿 BC 、 AC 翻折得到CM 、CN ，
DCN  2DCA ， DCM  2DCB ， CN  CD  CM  2r ，
MCN  2ACB  2，
过点C 作CQ  MN 于点Q ，则 MN  2NQ ， NCQ  1 MCN  ， CQN  90 ，
2
连接 AO 并延长交O 于点 P ，连接 BP ，则ABP  90 ，
 AB  AB ，
P  ACB  NCQ  ，
 AP  CN ， ABP  90  NQC ，
ABP  NQC (AAS ) ，
 AB  NQ  1 MN ，
2
 AB  1 ， AB 为定值．
MN2MN
方法二：连接OA ， OB ，
则OA  OB  r ， CN  MC  CD  2r ，
AOB  2ACB  MCN  2， OA  OB
CNCM
 1 ，
2
CNM ∽OAB ，
 AB MN
 1 ．
2