2023-2024学年山东省临沂市沂水实验中学九年级（上）期末数学试卷

这是一份2023-2024学年山东省临沂市沂水实验中学九年级（上）期末数学试卷，共31页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
1．（3分）下列各式中，计算结果为﹣4的是（ ）
A．﹣（﹣4）B．﹣|﹣4|C．（﹣2）2D．8÷（）
2．（3分）下列图案中既是中心对称图形，又是轴对称图形的是（ ）
A．B．
C．D．
3．（3分）一组数据共100个，分为6组，第1～4组的频数分别为10，14，16，20，第5组的频率为0.20，则第6组的频数为（ ）
A．20B．22C．24D．30
4．（3分）判断下列哪一组的a、b、c，可使二次函数y＝ax2+bx+c﹣5x2﹣3x+7在坐标平面上的图形有最高点（ ）
A．a＝0，b＝4，c＝8B．a＝7，b＝4，c＝﹣8
C．a＝8，b＝﹣4，c＝8D．a＝6，b＝﹣4，c＝﹣8
5．（3分）在某校“我的中国梦”演讲比赛中，有9名学生参加决赛，他们决赛的最终成绩各不相同．其中的一名学生想要知道自己能否进入前5名，不仅要了解自己的成绩，还要了解这9名学生成绩的（ ）
A．众数B．中位数C．平均数D．方差
6．（3分）如图，在由小正方形组成的网格中，小正方形的边长均为1，点A，B，O都在小正方形的顶点上，则∠AOB的正弦值是（ ）
A．B．C．D．
7．（3分）下列长度的三条线段能组成锐角三角形的是（ ）
A．2，3，4B．2，3，5C．3，4，4D．3，4，5
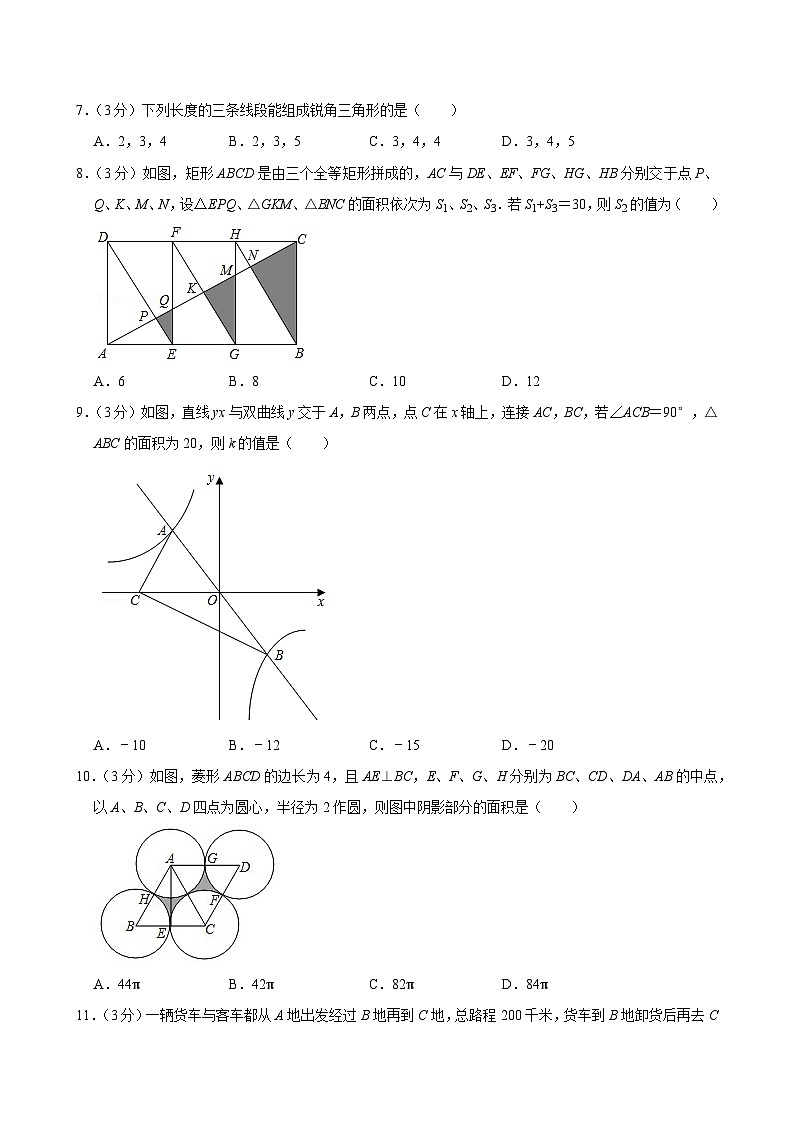
8．（3分）如图，矩形ABCD是由三个全等矩形拼成的，AC与DE、EF、FG、HG、HB分别交于点P、Q、K、M、N，设△EPQ、△GKM、△BNC的面积依次为S1、S2、S3．若S1+S3＝30，则S2的值为（ ）
A．6B．8C．10D．12
9．（3分）如图，直线yx与双曲线y交于A，B两点，点C在x轴上，连接AC，BC，若∠ACB＝90°，△ABC的面积为20，则k的值是（ ）
A．﹣10B．﹣12C．﹣15D．﹣20
10．（3分）如图，菱形ABCD的边长为4，且AE⊥BC，E、F、G、H分别为BC、CD、DA、AB的中点，以A、B、C、D四点为圆心，半径为2作圆，则图中阴影部分的面积是（ ）
A．44πB．42πC．82πD．84π
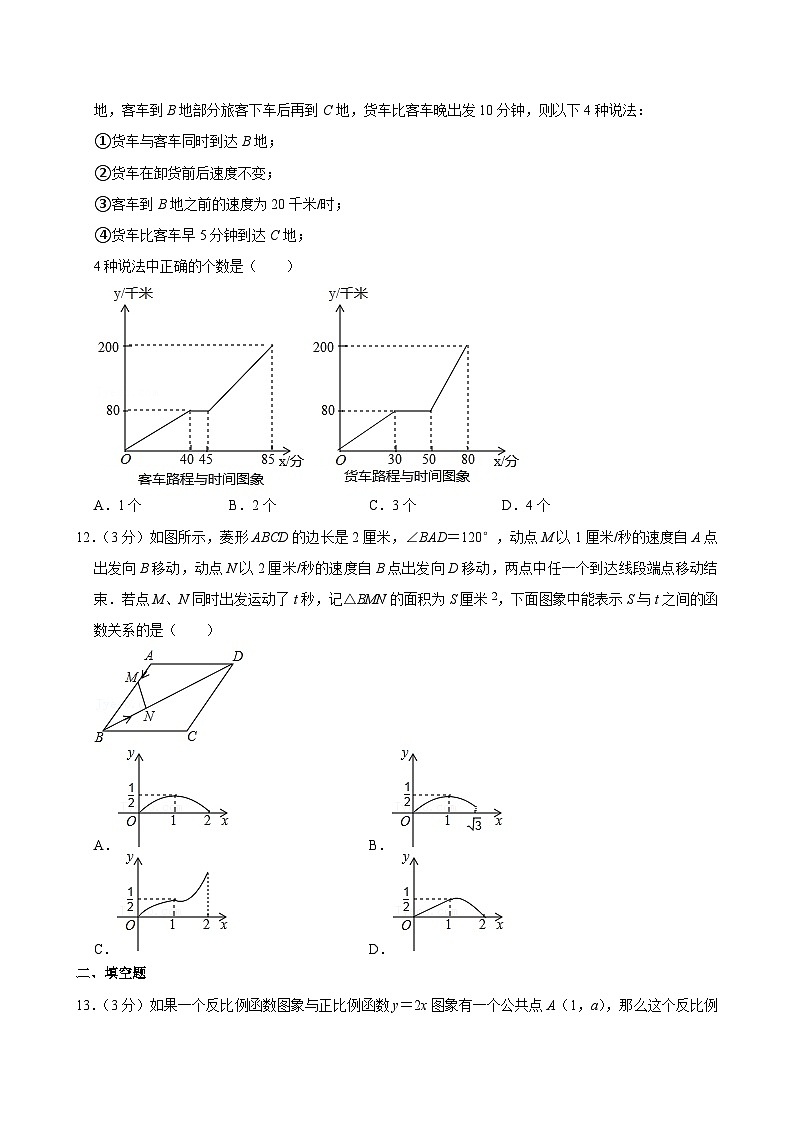
11．（3分）一辆货车与客车都从A地出发经过B地再到C地，总路程200千米，货车到B地卸货后再去C地，客车到B地部分旅客下车后再到C地，货车比客车晚出发10分钟，则以下4种说法：
①货车与客车同时到达B地；
②货车在卸货前后速度不变；
③客车到B地之前的速度为20千米/时；
④货车比客车早5分钟到达C地；
4种说法中正确的个数是（ ）
A．1个B．2个C．3个D．4个
12．（3分）如图所示，菱形ABCD的边长是2厘米，∠BAD＝120°，动点M以1厘米/秒的速度自A点出发向B移动，动点N以2厘米/秒的速度自B点出发向D移动，两点中任一个到达线段端点移动结束．若点M、N同时出发运动了t秒，记△BMN的面积为S厘米2，下面图象中能表示S与t之间的函数关系的是（ ）
A．B．
C．D．
二、填空题
13．（3分）如果一个反比例函数图象与正比例函数y＝2x图象有一个公共点A（1，a），那么这个反比例函数的解析式是 ．
14．（3分）设a，b是方程x2+x﹣2018＝0的两个实数根，则a2+2a+b的值为 ．
15．（3分）如图，一位同学用我们数学课本上采用的科学计算器进行计算，两次计算的按键顺序如下：，那么第一次按键输出的结果减去第二次按键输出结果的差等于 ．
16．（3分）如图，矩形纸片ABCD，AD＝4，AB＝3．如果点P在边BC上，将纸片沿AP折叠，使点B落在点E处，连接EC，当△EPC是直角三角形时，那么BP的长为 ．
17．（3分）已知如图，A（1，1）、B（4，2），CD为x轴上一条动线段，D在C点右边且CD＝1，当AC+CD+DB的最小值为 ．
三、解答题
18．解不等式组并把它的解集在数轴上表示出来．
19．如图，在四边形ABCD中，∠A＝90°，AD∥BC，BC＝BD，CE⊥BD，垂足为E．
（1）求证：△ABD≌△ECB；
（2）若AD＝4，CE＝3，求CD的长．
20．一种产品的进价为40元，某公司在销售这种产品时，每年总开支为100万元（不含进价）．经过若干年销售得知，年销售量y（万件）是销售单价x（元）的一次函数，并得到如下部分数据：
（1）求y关于x的函数关系式；
（2）写出该公司销售这种产品的年利润w（万元）关于销售单价x（元）的函数关系式；当销售单价x为何值时，年利润最大？
（3）试通过（2）中的函数关系式及其大致图象帮助该公司确定产品的销售单价范围，使年利润不低于60万元．
21．如图，在△ABC中，AB＝AC，AD⊥BC于点D，过点C作⊙O与边AB相切于点E，交BC于点F，CE为⊙O的直径．
（1）求证：OD⊥CE；
（2）若DF＝1，DC＝3，求AE的长．
22．某商店购进一批成本为每件30元的商品，经调查发现，该商品每天的销售量y（件）与销售单价x（元）之间满足一次函数关系，其图象如图所示．
（1）求该商品每天的销售量y与销售单价x之间的函数关系式；
（2）若商店按单价不低于成本价，且不高于50元销售，则销售单价定为多少，才能使销售该商品每天获得的利润w（元）最大？最大利润是多少？
（3）若商店要使销售量不少于70件，则销售单价最高为多少元？
23．如图，已知抛物线y＝ax2+2x+3与x轴交于A（﹣1，0），B两点，与y轴交于点C，直线l：y＝﹣2x+b与x轴、y轴分别交于点E，F，直线与抛物线有唯一交点G．
（1）求抛物线和直线的解析式．
（2）点H为抛物线对称轴上的动点，且到B，G的距离之和最小时，求点H的坐标，并求△HBG内切圆的半径．
（3）在第一象限内的抛物线上是否存在点K，使△KBC的面积最大？如果存在，求出△KBC的最大面积，如果不存在，请说明理由．
24．如图①，在平面直角坐标系中，抛物线y＝ax2+bx+3交x轴于A（﹣1，0）和B（5，0）两点，交y轴于点C，点D是线段OB上一动点，连接CD，将线段CD绕点D顺时针旋转90°得到线段DE，过点E作直线l⊥x轴于H，过点C作CF⊥l于点F．
（1）求抛物线解析式；
（2）如图②，当点F恰好在抛物线上时，求线段OD的长；
（3）在（2）的条件下：试探究在直线l上，是否存在点G，使∠EDG＝45°．若存在，请直接写出点G的坐标；若不存在，请说明理由．
2023-2024学年山东省临沂市沂水实验中学九年级（上）期末数学试卷
参考答案与试题解析
一、单选题
1．（3分）下列各式中，计算结果为﹣4的是（ ）
A．﹣（﹣4）B．﹣|﹣4|C．（﹣2）2D．8÷（）
【分析】根据有理数的运算方法，求出每个算式的值各是多少，判断出各式中，计算结果为﹣4的是哪个即可．
【解答】解：A、﹣（﹣4）＝4，不符合题意；
B、﹣|﹣4|＝﹣4，符合题意；
C、（﹣2）2＝4，不符合题意；
D、8÷（）＝﹣16，不符合题意；
故选：B．
【点评】此题主要考查了有理数的运算，要熟练掌握，注意明确有理数运算方法解答是解题关键．
2．（3分）下列图案中既是中心对称图形，又是轴对称图形的是（ ）
A．B．
C．D．
【分析】根据轴对称图形与中心对称图形的概念结合各图形的特点求解．
【解答】解：A、不是轴对称图形，是中心对称图形，不符合题意；
B、是轴对称图形，不是中心对称图形，不符合题意；
C、既是中心对称图形，又是轴对称图形的是，符合题意；
D、是轴对称图形，不是中心对称图形，不符合题意．
故选：C．
【点评】本题考查了中心对称图形与轴对称图形的概念．判断轴对称图形的关键是寻找对称轴，图形两部分沿对称轴折叠后可重合；判断中心对称图形是要寻找对称中心，图形旋转180度后与原图形重合．
3．（3分）一组数据共100个，分为6组，第1～4组的频数分别为10，14，16，20，第5组的频率为0.20，则第6组的频数为（ ）
A．20B．22C．24D．30
【分析】直接利用频数与频率的关系得出第5组的频数，进而得出答案．
【解答】解：∵一组数据共100个，第5组的频率为0.20，
∴第5组的频数是：100×0.20＝20，
∵一组数据共100个，分为6组，第1～4组的频数分别为10，14，16，20，
∴第6组的频数为：100﹣20﹣10﹣14﹣16﹣20＝20．
故选：A．
【点评】此题主要考查了频数与频率，正确得出第5组频数是解题关键．
4．（3分）判断下列哪一组的a、b、c，可使二次函数y＝ax2+bx+c﹣5x2﹣3x+7在坐标平面上的图形有最高点（ ）
A．a＝0，b＝4，c＝8B．a＝7，b＝4，c＝﹣8
C．a＝8，b＝﹣4，c＝8D．a＝6，b＝﹣4，c＝﹣8
【分析】将二次函数化为一般形式，使其二次项系数为负数即可．
【解答】解：y＝ax2+bx+c﹣5x2﹣3x+7＝（a﹣5）x2+（b﹣3）x+（c+7），
若使此二次函数图形有最高点，则图形的开口向下，即x2项系数为负数，
∴a﹣5＜0，
∴a＜5，
故选：A．
【点评】本题考查了二次函数的最值，理解二次函数系数与图象的关系是解题的关键．
5．（3分）在某校“我的中国梦”演讲比赛中，有9名学生参加决赛，他们决赛的最终成绩各不相同．其中的一名学生想要知道自己能否进入前5名，不仅要了解自己的成绩，还要了解这9名学生成绩的（ ）
A．众数B．中位数C．平均数D．方差
【分析】9人成绩的中位数是第5名的成绩．参赛选手要想知道自己是否能进入前5名，只需要了解自己的成绩以及全部成绩的中位数，比较即可．
【解答】解：由于总共有9个人，且他们的分数互不相同，第5的成绩是中位数，要判断是否进入前5名，故应知道中位数的多少．
故选：B．
【点评】此题主要考查统计的有关知识，主要包括平均数、中位数、众数、方差的意义．
6．（3分）如图，在由小正方形组成的网格中，小正方形的边长均为1，点A，B，O都在小正方形的顶点上，则∠AOB的正弦值是（ ）
A．B．C．D．
【分析】过点B作BC⊥OA于点C．先利用勾股定理求出BO、AO的长，再利用△AOB的面积求出BC的长，最后在直角△BCO中求出∠AOB的正弦值．
【解答】解：过点B作BC⊥OA于点C．
BO2，
AO2．
∵S△AOB2×2＝2，
∴AO•BC＝2．
∴BC．
∴sin∠AOB．
故选：B．
【点评】本题考查了解直角三角形，构造直角三角形，利用△的面积求出OA边上的高是解决本题的关键．
7．（3分）下列长度的三条线段能组成锐角三角形的是（ ）
A．2，3，4B．2，3，5C．3，4，4D．3，4，5
【分析】根据勾股定理求出以较短的两条边为直角边的三角形的斜边的长度，然后与较长的边进行比较作出判断即可．
【解答】解：A、∵4，2+3＞4，∴不能组成锐角三角形；
B、∵2+3＝5，∴不能组成三角形；
C、∵5＞4，3+4＞4，∴能组成锐角三角形；
D、∵5，是直角三角形，∴不能组成锐角三角形．
故选：C．
【点评】本题考查了勾股定理的逆定理，利用勾股定理求出直角三角形的斜边是解题的关键．
8．（3分）如图，矩形ABCD是由三个全等矩形拼成的，AC与DE、EF、FG、HG、HB分别交于点P、Q、K、M、N，设△EPQ、△GKM、△BNC的面积依次为S1、S2、S3．若S1+S3＝30，则S2的值为（ ）
A．6B．8C．10D．12
【分析】先证明△EPQ∽△GKM∽△BNC，再证明△AEQ∽△AGM得到，，所以S1S2，同理得到S3S2，所以S2S2＝30，从而得到S2的值．
【解答】解：∵矩形ABCD是由三个全等矩形拼成，
∴△ADE≌△EFG≌△GHB，
∴∠AED＝∠EGF＝∠GBH，
∴∠DEF＝∠FGH＝∠HBC，
∵FE∥HG∥BC，
∴∠AQE＝∠AMG＝∠ACB，
∴△EPQ∽△GKM∽△BNC，
∵QE∥MG，
∴△AEQ∽△AGM，
∴，
∴（）2，
∴S1S2，
∵MG∥CB，
∴△AGM∽△ABC，
∴，
∴（）2，
∴S3S2，
∵S1+S3＝30，
∴S2S2＝30，
∴S2＝12．
故选：D．
【点评】本题考查了相似三角形的判定与性质：在判定两个三角形相似时，应注意利用图形中已有的公共角、公共边等隐含条件，以充分发挥基本图形的作用，寻找相似三角形的一般方法是通过作平行线构造相似三角形，灵活运用相似三角形的性质表示线段之间的关系；也考查了矩形的性质．
9．（3分）如图，直线yx与双曲线y交于A，B两点，点C在x轴上，连接AC，BC，若∠ACB＝90°，△ABC的面积为20，则k的值是（ ）
A．﹣10B．﹣12C．﹣15D．﹣20
【分析】设点A（a，a），利用S△ACB（yA+|yB|）＝20，构建方程即可解决问题．
【解答】解：设点A（a，a），
则OAa，
∵点C在x轴上一点，∠ACB＝90°，且△ACB的面积为20，
∴OA＝OB＝OCa，
∴S△ACBOC×（yA+|yB|）（a）×（a）＝20，
解得a＝±3（舍弃3），
∴点A为（﹣3，4），
∴k＝﹣3×4＝﹣12，
故选：B．
【点评】本题考查一次函数与反比例函数的交点问题，解题的关键是明确题意，找出所求问题需要的条件，利用数形结合的思想解答问题．
10．（3分）如图，菱形ABCD的边长为4，且AE⊥BC，E、F、G、H分别为BC、CD、DA、AB的中点，以A、B、C、D四点为圆心，半径为2作圆，则图中阴影部分的面积是（ ）
A．44πB．42πC．82πD．84π
【分析】由图形可知，阴影部分的面积是菱形ABCD的面积减去半径为2的整圆的面积，然后根据题目中的数据可以计算AE的长，然后代入数据计算即可解答本题．
【解答】解：由已知可得，
AB＝BC＝AC＝4，
∵点E为BC的中点，
∴AE⊥BC，并且平分BC，
∴AE2，
由图可得，阴影部分的面积是平行四边形ABCD的面积﹣（扇形AHG的面积+扇形BHE的面积+扇形CEF的面积+扇形DGF的面积）＝平行四边形ABCD的面积﹣圆A的面积，
∴图中阴影部分的面积是：4π×22＝84π，
故选：D．
【点评】本题考查扇形面积的计算、菱形的性质，解答本题的关键是明确题意，可以发现四个扇形的面积之和正好是半径为2的整圆的面积．
11．（3分）一辆货车与客车都从A地出发经过B地再到C地，总路程200千米，货车到B地卸货后再去C地，客车到B地部分旅客下车后再到C地，货车比客车晚出发10分钟，则以下4种说法：
①货车与客车同时到达B地；
②货车在卸货前后速度不变；
③客车到B地之前的速度为20千米/时；
④货车比客车早5分钟到达C地；
4种说法中正确的个数是（ ）
A．1个B．2个C．3个D．4个
【分析】①由函数图可以得出货车到达B地用时30分钟，客车到达B地用时40分钟，根据货车比客车晚出发10分钟就可以得出货车与客车同时到达B地；
②分别求出货车卸货前后的速度并作比较就可以得出结论；
③由路程÷时间＝速度就可以得出结论；
④由函数图象可以得出货车到达C地的时间是80分钟，客车到达C地的时间是85分钟就可以得出，但是客车先出发了10分钟，故货车比客车晚5分钟到达C地．
【解答】解：①函数图可以得出货车到达B地用时30分钟，客车到达B地用时40分钟，
∵车比客车晚出发10分钟，
∴货车与客车同时到达B地．故正确
②货车在卸货前的速度为：80÷0.5＝160千米/时，
货车在卸货后的速度为：120÷0.5＝240千米/时．
∵160≠240，
∴货车在卸货前后速度不相等．故错误；
③客车到B地之前的速度为：80120千米/时≠20千米/时．故错误；
④由函数图象可以得出货车到达C地所有时间是80分钟，客车到达C地所用时间是85分钟，
∵客车先出发了10分钟，
∴货车是客车出发90分钟后到达的C地，
∴货车比客车晚5分钟到达C地．故错误．
故选：A．
【点评】本题考查了行程问题的数量关系：速度＝路程÷时间的运用，一次函数的图象的性质的运用，有理数大小比较的运用，解答时分析清楚一次函数图象的数据的含义是关键．
12．（3分）如图所示，菱形ABCD的边长是2厘米，∠BAD＝120°，动点M以1厘米/秒的速度自A点出发向B移动，动点N以2厘米/秒的速度自B点出发向D移动，两点中任一个到达线段端点移动结束．若点M、N同时出发运动了t秒，记△BMN的面积为S厘米2，下面图象中能表示S与t之间的函数关系的是（ ）
A．B．
C．D．
【分析】连接AC与BD交于点O，作MH⊥BD，垂足为H，根据菱形的性质以及题目给出的条件可得BOcm，进而得出BDcm，根据题意可知AM＝tcm，BN＝2tcm，根据题意得出t的取值范围，再根据三角形的面积公式得出S与t之间的函数关系式即可得出正确选项．
【解答】解：如图，连接AC与BD交于点O，作MH⊥BD，垂足为H，
∵ABCD是菱形，∠BAD＝120°，
∴∠BAC＝60°，∠ABO＝30°，
∴BO＝AB•cs30°（cm），
∴BD（cm），
根据s＝vt可知，AM＝t（cm），BN＝2t（cm），
∵0≤AM≤2，得0≤t≤2，，
∴，
∵在△BMH中，BN＝2t，MH＝BM•sin30°，
∴（），
此函数的图象为开口方向向下的抛物线的一部分，且图象两个端点的横坐标分别为0，．
故选：B．
【点评】本题主要考查了动点问题的函数图象，利用图形的关系求函数的解析式，注意数形结合是解决本题的关键．
二、填空题
13．（3分）如果一个反比例函数图象与正比例函数y＝2x图象有一个公共点A（1，a），那么这个反比例函数的解析式是 y ．
【分析】根据题意可以求得点A的坐标，再将点A的坐标代入反比例函数解析式即可解答本题．
【解答】解：将x＝1代入y＝2x，得y＝2，
∴点A（1，2），
设反比例函数解析式为y，
∵一个反比例函数图象与正比例函数y＝2x图象有一个公共点A（1，2），
∴2．
解得，k＝2，
即反比例函数解析式为y，
故答案为：y．
【点评】本题考查反比例函数与一次函数的交点问题，解答本题的关键是明确题意，找出所求问题需要的条件，求出相应的函数解析式．
14．（3分）设a，b是方程x2+x﹣2018＝0的两个实数根，则a2+2a+b的值为 2017 ．
【分析】根据一元二次方程的解及根与系数的关系可得出a2+a＝2018、a+b＝﹣1，将其代入a2+2a+b＝（a2+a）+（a+b）中即可求出结论．
【解答】解：∵a，b是方程x2+x﹣2018＝0的两个实数根，
∴a2+a＝2018，a+b＝﹣1，
∴a2+2a+b＝（a2+a）+（a+b）＝2018﹣1＝2017．
故答案为：2017．
【点评】本题考查了根与系数的关系以及一元二次方程的解，根据一元二次方程的解及根与系数的关系找出a2+a＝2018、a+b＝﹣1是解题的关键．
15．（3分）如图，一位同学用我们数学课本上采用的科学计算器进行计算，两次计算的按键顺序如下：，那么第一次按键输出的结果减去第二次按键输出结果的差等于 2 ．
【分析】利用科学计算器的使用规则把有理数混合运算，再计算．
【解答】解：第一次运算：，
第二次运算：，
∴第一次按键输出的结果减去第二次按键输出结果的差为：67﹣65＝2，
故答案为：2．
【点评】此题考查了科学计算器的使用计算，解题的关键是正确使用科学计算器．
16．（3分）如图，矩形纸片ABCD，AD＝4，AB＝3．如果点P在边BC上，将纸片沿AP折叠，使点B落在点E处，连接EC，当△EPC是直角三角形时，那么BP的长为 1.5或3 ．
【分析】分类讨论∠PEC＝90°、∠EPC＝90°，画出对应的图形即可求解．
【解答】解：若∠PEC＝90°，如图1：
∵∠AEP＝∠B＝∠PEC＝90°，
∴A、E、C三点共线，
由题意得：，
设EP＝BP＝x，则CP＝BC﹣BP＝4﹣x，
由翻折可知：AE＝AB＝3，
∴CE＝AC﹣AE＝2，
∴（4﹣x）2＝x2+22，
解得：x＝1.5，
∴BP＝1.5；
若∠EPC＝90°，如图2：
则四边形ABPE是矩形，
由翻折可知：BP＝EP，
∴四边形ABPE是正方形，
∴BP＝AB＝3，
综上所述：BP＝1.5或BP＝3，
故答案为：1.5或3．
【点评】本题考查了翻折变换（折叠问题），勾股定理，矩形的性质，掌握折叠的性质是解答本题的关键．
17．（3分）已知如图，A（1，1）、B（4，2），CD为x轴上一条动线段，D在C点右边且CD＝1，当AC+CD+DB的最小值为 ．
【分析】涉及了平行四边形的判定与性质、两点之间线段最短等知识点，将点A（1，1）向右平移1个单位长度得到点A′（2，1）构造平行四边形ACDA′是解题即可．
【解答】解：将点A（1，1）向右平移1个单位长度得到点A′（2，1），作点A′（2，1）关于x轴的对称点A′′（2，﹣1），连接A″，B，与x轴的交点即为点D，此时AC+CD+DB的值最小，如图所示：
∵AA′＝CD＝1，且AA′∥CD，
∴四边形ACDA′为平行四边形，
∴AC＝A′D，
∵点A′（2，1）关于x轴的对称点为A″，
∴A′D＝A″D，
∴AC+CD+DB＝A″D+DB+1≥A″B+1，
∵，
∴AC+CD+DB的最小值为：，
故答案为：．
【点评】本题考查了“将军饮马”求最值的模型，涉及了平行四边形的判定与性质、两点之间线段最短等知识点，将点A（1，1）向右平移1个单位长度得到点A′（2，1）构造平行四边形ACDA′是解题关键．
三、解答题
18．解不等式组并把它的解集在数轴上表示出来．
【分析】分别解两个不等式得到x＞﹣2和x≤3，再利用数轴表示解集，然后根据大小小大中间找确定不等式组的解集．
【解答】解：
解不等式①得x＞﹣2，
解不等式②得x≤3，
数轴表示解集为：
所以不等式组的解集是﹣2＜x≤3．
【点评】本题考查了一元一次不等式组：解一元一次不等式组时，一般先求出其中各不等式的解集，再求出这些解集的公共部分，利用数轴可以直观地表示不等式组的解集．解集的规律：同大取大；同小取小；大小小大中间找；大大小小找不到．
19．如图，在四边形ABCD中，∠A＝90°，AD∥BC，BC＝BD，CE⊥BD，垂足为E．
（1）求证：△ABD≌△ECB；
（2）若AD＝4，CE＝3，求CD的长．
【分析】（1）由AD∥BC得∠ADB＝∠EBC，由CE⊥BD得∠A＝∠BEC＝90°，根据AAS可证△ABD≌△ECB；
（2）根据全等三角形的性质和勾股定理解答即可．
【解答】证明：（1）∵AD∥BC，
∴∠ADB＝∠EBC，
∵CE⊥BD，∠A＝90°，
∴∠A＝∠BEC＝90°，
在△ABD和△ECB中，
，
∴△ABD≌△ECB（AAS）；
（2）∵△ABD≌△ECB，
∴AB＝CE＝3，
∵AD＝4，
∴在Rt△ABD中，由勾股定理可得：BD＝5，
∵△ABD≌△ECB，
∴AD＝BE＝4，
∴DE＝BD﹣BE＝1，
∴在Rt△CDE中，由勾股定理得：CD．
【点评】本题主要考查梯形、全等三角形的判定和性质、勾股定理的运用，根据已知条件推得能证全等的条件是关键．
20．一种产品的进价为40元，某公司在销售这种产品时，每年总开支为100万元（不含进价）．经过若干年销售得知，年销售量y（万件）是销售单价x（元）的一次函数，并得到如下部分数据：
（1）求y关于x的函数关系式；
（2）写出该公司销售这种产品的年利润w（万元）关于销售单价x（元）的函数关系式；当销售单价x为何值时，年利润最大？
（3）试通过（2）中的函数关系式及其大致图象帮助该公司确定产品的销售单价范围，使年利润不低于60万元．
【分析】（1）根据表中的已知点的坐标利用待定系数法确定直线的解析式即可；
（2）根据总利润＝单件利润×销量列出函数关系式配方后即可确定最值；
（3）令利润等于60求得相应的自变量的值即可确定销售单价的范围．
【解答】解：（1）设y＝kx+b，把（60，5），（80，4）代入得：，
解得：，
故答案为：yx+8；
（2）该公司年利润w＝（x+8）（x﹣40）﹣100（x﹣100）2+80，
当x＝100时，该公司年利润最大值为80万元；
（3）由题意得：（x﹣100）2+80＝60，
解得：x1＝80，x2＝120，
故该公司确定销售单价x的范围是：80≤x≤120．
根据函数图象可得：当80≤x≤120时，
该公司产品的利润不低于60万元．
【点评】本题考查了二次函数的应用，解题时把实际问题转化为二次函数，再对二次函数进行实际应用．此题为数学建模题，借助二次函数解决实际问题．
21．如图，在△ABC中，AB＝AC，AD⊥BC于点D，过点C作⊙O与边AB相切于点E，交BC于点F，CE为⊙O的直径．
（1）求证：OD⊥CE；
（2）若DF＝1，DC＝3，求AE的长．
【分析】（1）⊙O与边AB相切于点E，且 CE为⊙O的直径，得到CE⊥AB，由等腰三角形的性质三线合一得到BD＝DC，根据三角形的中位线的性质得到结论；
（2）连接EF，由CE为⊙O的直径，且点F在⊙O上，得到∠EFC＝90°，又因为 CE⊥AB，得到∠BEF+∠FEC＝∠FEC+∠ECF＝90°，推出∠BEF＝∠ECF，于是得到tan∠BEF＝tan∠ECF，得到等积式，求得EF＝2，由勾股定理得BE，再根据平行线分线段成比例，列出比例式求解．
【解答】解：（1）∵⊙O与边AB相切于点E，且 CE为⊙O的直径，
∴CE⊥AB，
∵AB＝AC，AD⊥BC，
∴BD＝DC，
又∵OE＝OC，
∴OD∥EB，
∴OD⊥CE；
（2）连接EF，
∵CE为⊙O的直径，且点F在⊙O上，∴∠EFC＝90°，
∵CE⊥AB，
∴∠BEC＝90°．
∴∠BEF+∠FEC＝∠FEC+∠ECF＝90°，
∴∠BEF＝∠ECF，
∴tan∠BEF＝tan∠ECF
∴，
又∵DF＝1，BD＝DC＝3，
∴BF＝2，FC＝4，
∴EF＝2，
∵∠EFC＝90°，
∴∠BFE＝90°，
由勾股定理，得，
∵EF∥AD，
∴，
∴．
【点评】本题考查了切线的性质，圆周角定理，锐角三角函数，勾股定理，平行线的性质，正确的作出辅助线是解题的关键．
22．某商店购进一批成本为每件30元的商品，经调查发现，该商品每天的销售量y（件）与销售单价x（元）之间满足一次函数关系，其图象如图所示．
（1）求该商品每天的销售量y与销售单价x之间的函数关系式；
（2）若商店按单价不低于成本价，且不高于50元销售，则销售单价定为多少，才能使销售该商品每天获得的利润w（元）最大？最大利润是多少？
（3）若商店要使销售量不少于70件，则销售单价最高为多少元？
【分析】（1）将点（30，100）、（45，70）代入一次函数表达式，即可求解；
（2）由题意得w＝（x﹣30）（﹣2x+160）＝﹣2（x﹣55）2+1250，即可求解；
（3）由题意得﹣2x+160≥70，解不等式即可得到结论．
【解答】解：（1）设y与销售单价x之间的函数关系式为：y＝kx+b，
将点（30，100）、（45，70）代入一次函数表达式得：，
解得：，
故函数的表达式为：y＝﹣2x+160；
（2）由题意得：w＝（x﹣30）（﹣2x+160）＝﹣2（x﹣55）2+1250，
∵﹣2＜0，故当x＜55时，w随x的增大而增大，而30≤x≤50，
∴当x＝50时，w有最大值，此时，w＝1200，
故销售单价定为50元时，该商店每天的利润最大，最大利润1200元；
（3）由题意得：﹣2x+160≥70，
解得：x≤45，
商店要使销售量不少于70件，则销售单价最高为45元．
【点评】此题主要考查了二次函数的应用以及一元二次不等式的应用、待定系数法求一次函数解析式等知识，正确利用销量×每件的利润＝w得出函数关系式是解题关键．
23．如图，已知抛物线y＝ax2+2x+3与x轴交于A（﹣1，0），B两点，与y轴交于点C，直线l：y＝﹣2x+b与x轴、y轴分别交于点E，F，直线与抛物线有唯一交点G．
（1）求抛物线和直线的解析式．
（2）点H为抛物线对称轴上的动点，且到B，G的距离之和最小时，求点H的坐标，并求△HBG内切圆的半径．
（3）在第一象限内的抛物线上是否存在点K，使△KBC的面积最大？如果存在，求出△KBC的最大面积，如果不存在，请说明理由．
【分析】（1）用待定系数法可得抛物线的解析式为y＝﹣x2+2x+3；根据直线y＝﹣2x+b与抛物线有唯一交点G，知x2﹣4x+b﹣3＝0有两个相等的实数解，即16﹣4（b﹣3）＝0，得b＝7，故直线的解析式为y＝﹣2x+7；
（2）求出G（2，3），由HB＝HA，可知当G，H，A共线时，HB+HG最小，由A（﹣1，0），G（2，3）可得直线AG解析式为y＝x+1，令x＝1得y＝2，故H（1，2）；可证△GHB是直角三角形，设△HBG内切圆的半径为r，根据2S△BHG＝BH•HG＝（HG+BG+BH）•r，即可得△HBG内切圆的半径为；
（3）过K作KQ∥y轴交BC于Q，设K（m，﹣m2+2m+3），可得Q（m，﹣m+3），KQ＝﹣m2+2m+3﹣（﹣m+3）＝﹣m2+3m，故S△KBC（﹣m2+3m）×3（m）2，由二次函数性质可得答案．
【解答】解：（1）把A（﹣1，0）代入y＝ax2+2x+3得：
0＝a﹣2+3，
解得a＝﹣1，
∴抛物线的解析式为y＝﹣x2+2x+3；
∵直线y＝﹣2x+b与抛物线有唯一交点G，
∴﹣x2+2x+3＝﹣2x+b有两个相等的实数解，
即x2﹣4x+b﹣3＝0有两个相等的实数解，
∴Δ＝0，即16﹣4（b﹣3）＝0，
解得b＝7，
∴直线的解析式为y＝﹣2x+7；
（2）在y＝﹣x2+2x+3中，令y＝0得x＝﹣1或x＝3，
∴B（3，0），
∴抛物线y＝﹣x2+2x+3的对称轴为直线x1，
由得：，
∴G（2，3），
∵点H为抛物线对称轴上的点，
∴HB＝HA，
∴HB+HG＝HA+HG，
∴当G，H，A共线时，HB+HG最小，最小值即为AG的长度；
如图：
由A（﹣1，0），G（2，3）可得直线AG解析式为y＝x+1，
在y＝x+1中，令x＝1得y＝2，
∴H（1，2）；
∴OH＝OA＝2，
∴△AOH是等腰直角三角形，
∴∠AHO＝45°，
由对称性可得∠BHO＝45°，
∴∠GHB＝90°，即△GHB是直角三角形，
∵G（2，3），H（1，2），B（3，0），
∴HG，BG，BH＝2，
设△HBG内切圆的半径为r，
∴2S△BHG＝BH•HG＝（HG+BG+BH）•r，
∴r，
∴△HBG内切圆的半径为；
（3）存在点K，使△KBC的面积最大，理由如下：
过K作KQ∥y轴交BC于Q，如图：
设K（m，﹣m2+2m+3），
在y＝﹣x2+2x+3中，令x＝0得y＝3，
∴C（0，3），
由B（3，0），C（0，3）可得y＝﹣x+3，
∴Q（m，﹣m+3），
∴KQ＝﹣m2+2m+3﹣（﹣m+3）＝﹣m2+3m，
∴S△KBC（﹣m2+3m）×3（m）2，
∴当m时，S△KBC取最大值，
∴△KBC的最大面积是．
【点评】本题考查二次函数的综合应用，涉及待定系数法，对称变换，函数图象上点坐标的特征等，解题的关键是掌握待定系数法，求出函数解析式．
24．如图①，在平面直角坐标系中，抛物线y＝ax2+bx+3交x轴于A（﹣1，0）和B（5，0）两点，交y轴于点C，点D是线段OB上一动点，连接CD，将线段CD绕点D顺时针旋转90°得到线段DE，过点E作直线l⊥x轴于H，过点C作CF⊥l于点F．
（1）求抛物线解析式；
（2）如图②，当点F恰好在抛物线上时，求线段OD的长；
（3）在（2）的条件下：试探究在直线l上，是否存在点G，使∠EDG＝45°．若存在，请直接写出点G的坐标；若不存在，请说明理由．
【分析】（1）用待定系数法求抛物线解析式即可；
（2）先求出点F（4，3），在判断出△OCD≌△HDE，再做简单的计算即可；
（3）先求出E（4，1），再根据直线之间的关系用待定系数法依次求出，直线CE解析式为yx+3，直线DG2的解析式为yx+3，即可．
【解答】解：（1）∵抛物线y＝ax2+bx+3交x轴于A（﹣1，0），B（5，0），
∴，
∴，
∴抛物线yx2x+3，
（2）∵点F恰好在抛物线上，C（0，3），
∴F的纵坐标为3，
把y＝3代入yx2x+3，得3x2x+3，
∴x＝0，或x＝4，
∴F（4，3），
∴OH＝4，
∵∠CDE＝90°，
∴∠ODC+∠HDC＝90°，
∴∠OCD＝∠HDE，
在△OCD和△HDE中，
，
∴△OCD≌△HDE，
∴DH＝OC＝3，
∴OD＝4﹣3＝1；
（3）存在，如图，
连接CE，
∵CD＝DE，∠CDE＝90°，
∴∠CED＝45°，
过点D作DG1∥CE，过点D作DG2⊥CE，
∴∠EDG1＝45°，∠EDG2＝45°，
∵EH＝OD＝1，OH＝4，
∴E（4，1），
∵C（0，3），
∴直线CE解析式为yx+3，
设直线DG2的解析式为yx+m，
∵D（1，0），
∴01+m，
∴m，
∴直线DG2的解析式为yx+3，
当x＝4时，y4，
∴G1（4，），
设直线DG1的解析式为y＝2x+n，
∵D（1，0），
∴0＝2×1+n，
∴n＝﹣2，
∴直线DG1的解析式为y＝2x﹣2．
当x＝4时，y＝6，
∴G2（4，6）．
【点评】此题是二次函数综合题，主要考查了用待定系数法求抛物线，直线解析式，三角形全等的判定和性质，解本题的关键是寻找出直线之间的关系来确定直线解析式．
声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布日期：2024/12/26 14:27:53；用户：刘亚君；邮箱：99197645@qq.cm；学号：2798877销售单价x（元）
50
60
70
80
年销售量y（万件）
5.5
5
4.5
4
题号
1
2
3
4
5
6
7
8
9
10
11
答案
B
C
A
A
B
B
C
D
B
D
A
题号
12
答案
B
销售单价x（元）
50
60
70
80
年销售量y（万件）
5.5
5
4.5
4