2023-2024学年广东省汕头市龙湖区八年级（上）期末数学试卷

这是一份2023-2024学年广东省汕头市龙湖区八年级（上）期末数学试卷，共7页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1．（3分）中国新能源汽车发展迅速，下列各图是国产新能源汽车图标，不是轴对称图形的是（ ）
A．B．
C．D．
2．（3分）分式有意义的条件是（ ）
A．x＝﹣3B．x≠﹣3C．x≠3D．x≠0
3．（3分）下列多边形中，内角和等于360°的是（ ）
A．B．
C．D．
4．（3分）下面运算正确的是（ ）
A．7a2b﹣5a2b＝2B．x8÷x4＝x2
C．（a﹣b）2＝a2﹣b2D．（2x2）3＝8x6
5．（3分）袁老师在课堂上组织学生用小棍摆三角形，小棍的长度有10cm，15cm，20cm和25cm四种规格，小朦同学已经取了10cm和15cm两根木棍，那么第三根木棍不可能取（ ）
A．10cmB．15cmC．20cmD．25cm
6．（3分）我国古代数学家祖冲之发现的圆周率的分数近似值，称为密率，比π的值只大0.0000003，0.0000003这个数用科学记数法可表示为（ ）
A．3×10﹣7B．0.3×10﹣7C．0.3×10﹣6D．3×10﹣6
7．（3分）阅读以下作图步骤：
①在OA和OB上分别截取OC，OD，使OC＝OD；
②分别以C，D为圆心，以大于CD的长为半径作弧，两弧在∠AOB内交于点M；
③作射线OM，连接CM，DM，如图所示．
根据以上作图，一定可以推得的结论是（ ）
A．∠1＝∠2且CM＝DMB．∠1＝∠3且CM＝DM
C．∠1＝∠2且OD＝DMD．∠2＝∠3且OD＝DM
8．（3分）如图，从边长为a的大正方形中剪掉一个边长为b的小正方形，将阴影部分沿虚线剪开，拼成右边的矩形．根据图形的变化过程写出的一个正确的等式是（ ）
A．（a﹣b）2＝a2﹣2ab+b2B．a（a﹣b）＝a2﹣ab
C．（a﹣b）2＝a2﹣b2D．a2﹣b2＝（a+b）（a﹣b）
9．（3分）如图所示，在△ABC中，∠C＝90°，∠A＝30°，DE为AB的中垂线，AD＝12，则CD的长是（ ）
A．3B．4C．6D．8
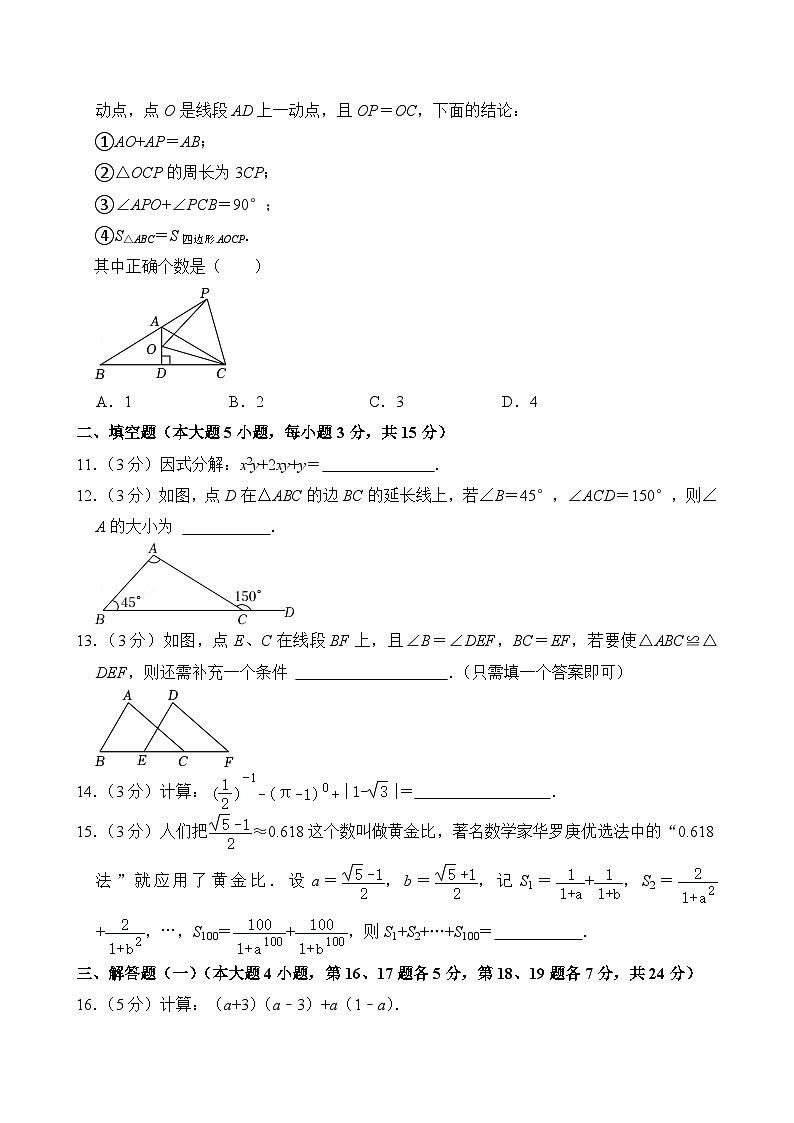
10．（3分）如图，已知△ABC中高AD恰好平分边BC，∠B＝30°，点P是BA延长线上一动点，点O是线段AD上一动点，且OP＝OC，下面的结论：
①AO+AP＝AB；
②△OCP的周长为3CP；
③∠APO+∠PCB＝90°；
④S△ABC＝S四边形AOCP．
其中正确个数是（ ）
A．1B．2C．3D．4
二、填空题（本大题5小题，每小题3分，共15分）
11．（3分）因式分解：x2y+2xy+y＝ ．
12．（3分）如图，点D在△ABC的边BC的延长线上，若∠B＝45°，∠ACD＝150°，则∠A的大小为 ．
13．（3分）如图，点E、C在线段BF上，且∠B＝∠DEF，BC＝EF，若要使△ABC≌△DEF，则还需补充一个条件 ．（只需填一个答案即可）
14．（3分）计算：＝ ．
15．（3分）人们把≈0.618这个数叫做黄金比，著名数学家华罗庚优选法中的“0.618法”就应用了黄金比．设a＝，b＝，记S1＝+，S2＝+，…，S100＝+，则S1+S2+…+S100＝ ．
三、解答题（一）（本大题4小题，第16、17题各5分，第18、19题各7分，共24分）
16．（5分）计算：（a+3）（a﹣3）+a（1﹣a）．
17．（5分）如图，C是BD的中点，AB＝ED，AC＝EC．求证：∠B＝∠D．
18．（7分）解分式方程：+2＝．
19．（7分）先化简，再求值，其中a＝2024．
四、解答题（二）（本大题3小题，每小题9分，共27分）
20．（9分）如图，在△ABC中，AB＝AC，AD为△ABC的角平分线．以点A圆心，AD长为半径画弧，与AB，AC分别交于点E，F，连接DE，DF．
（1）求证：△ADE≌△ADF；
（2）若∠BAC＝80°，求∠BDE的度数．
21．（9分）如图，△ABC三个顶点的坐标分别是A（1，1），B（4，2），C（3，4）．
（1）请画出△ABC关于x轴对称的图形△A1B1C1，并写出点C1的坐标；
（2）求△ABC的面积；
（3）在x轴上求一点P，使PA+PB的值最小，通过画图直接画出点P．
22．（9分）某欧洲客商准备采购一批特色商品，下面是一段对话：
甲：用16000元采购A型商品的件数是用7500元采购B型商品的件数的2倍；
乙：一件A型商品的进价比一件B型商品的进价多10元．
（1）根据对话信息，求一件A，B型商品的进价分别为多少元；
（2）若该欧洲客商购进A，B型商品共160件进行试销，其中A型商品的件数不大于B型商品的件数，且不小于78件，则共有哪几种进货方式？
五、解答题（三）（本大题2小题，每小题12分，共24分）
23．（12分）综合与实践
数学模型可以用来解决一类问题，是数学应用的基本途径．通过探究图形的变化规律，再结合其他数学知识的内在联系，最终可以获得宝贵的数学经验，并将其运用到更广阔的数学天地．
（1）发现问题：如图1，在△ABC和△AEF中，AB＝AC，AE＝AF，∠BAC＝∠EAF＝30°，连接BE，CF，延长BE交CF于点D．则BE与CF的数量关系： ，∠BDC＝ °；
（2）类比探究：如图2，在△ABC和△AEF中，AB＝AC，AE＝AF，∠BAC＝∠EAF＝120°，连接BE，CF，延长BE，FC交于点D．请猜想BE与CF的数量关系及∠BDC的度数，并说明理由；
（3）拓展延伸：如图3，△ABC和△AEF均为等腰直角三角形，∠BAC＝∠EAF＝90°，连接BE，CF，且点B，E，F在一条直线上，过点A作AM⊥BF，垂足为点M．则BF，CF，AM之间的数量关系： ．
24．（12分）综合与实践：【积累经验】
我们在第十三章《全等三角形》中学习了全等三角形的性质和判定，在一些探究题中经常用以上知识转化角和边，进而解决问题．例如：我们在解决：“如图1，在△ABC中，∠ACB＝90°，AC＝BC，线段DE经过点C，且AD⊥DE于点D，BE⊥DE于点E．
求证：AD＝CE，CD＝BE这个问题时，只要证明△ADC≌△CEB即可得到解决．
（1）请写出证明过程：
【类比应用】
（2）如图2，△ABC在平面直角坐标系中，∠ACB＝90°，AC＝BC，点A的坐标为（2，1），点C的坐标为（4，2），求点B的坐标．
【拓展提升】
（3）如图3，在平面直角坐标系中，点A的坐标为（2，﹣1），点B的坐标为（5，0），以AB为一边构造等腰直角三角形ABC，直接写出在第一象限内满足条件的所有点C的坐标 ．
2023-2024学年广东省汕头市龙湖区八年级（上）期末数学试卷
参考答案
一、选择题（本大题10小题，每小题3分，共30分）
1．B；2．B；3．B；4．D；5．D；6．A；7．A；8．D；9．C；10．D；
二、填空题（本大题5小题，每小题3分，共15分）
11．y（x+1）2；12．105°；13．AB＝DE（答案不唯一）；14．；15．5050；
三、解答题（一）（本大题4小题，第16、17题各5分，第18、19题各7分，共24分）
16．a﹣9．；17．见解析．；18． ；19．a﹣1；2023．；
四、解答题（二）（本大题3小题，每小题9分，共27分）
20． ；21．（1）作图见解析部分，C1（3，﹣4）；
（2）3.5；
（3）作图见解析部分．；22．（1）一件A型商品的进价是160元，一件B型商品的进价是150元；
（2）共有3种进货方式，
方案1：购进78件A型商品，82件B型商品；
方案2：购进79件A型商品，81件B型商品；
方案3：购进80件A型商品，80件B型商品．；
五、解答题（三）（本大题2小题，每小题12分，共24分）
23．BE＝CF；30；BF＝CF+2AM；24．（1，2）或（4，3）或（3，1）；