










所属成套资源:人教版数学八年级下学期课件PPT+分层练习(原卷版+解析版)整套(含单元复习资料)
人教版(2024)18.1.2 平行四边形的判定获奖课件ppt
展开
这是一份人教版(2024)18.1.2 平行四边形的判定获奖课件ppt,文件包含人教版数学八年级下册18122《平行四边形的判定》第2课时同步课件pptx、人教版数学八年级下册18122《平行四边形的判定》第2课时分层练习原卷版-docx、人教版数学八年级下册18122《平行四边形的判定》第2课时分层练习解析版docx等3份课件配套教学资源,其中PPT共24页, 欢迎下载使用。
高铁被外媒誉为我国新四大发明之一,我们知道铁路的两条直铺的铁轨互相平行,那么铁路工人是怎样的确保它们平行的呢?
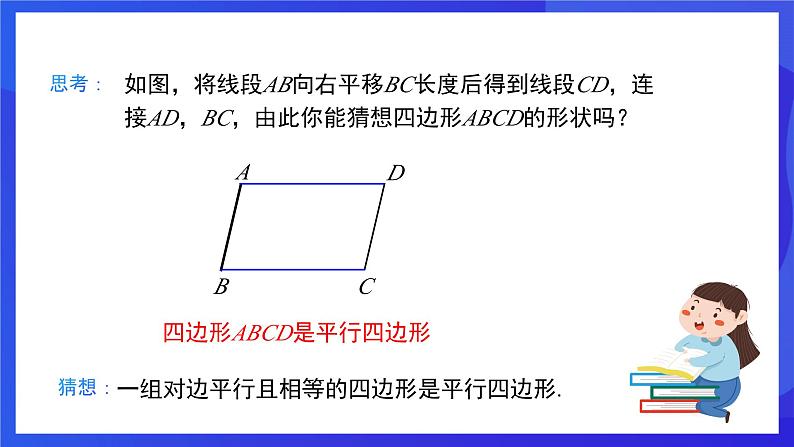
如图,将线段AB向右平移BC长度后得到线段CD,连接AD,BC,由此你能猜想四边形ABCD的形状吗?
四边形ABCD是平行四边形
一组对边平行且相等的四边形是平行四边形.
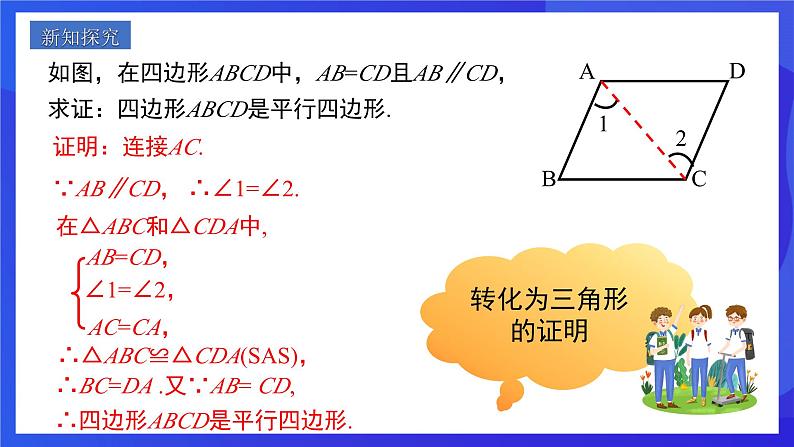
如图,在四边形ABCD中,AB=CD且AB∥CD,求证:四边形ABCD是平行四边形.
证明:连接AC.∵AB∥CD, ∴∠1=∠2.
在△ABC和△CDA中,
∴△ABC≌△CDA(SAS),
∴BC=DA .又∵AB= CD,
∴四边形ABCD是平行四边形.
几何语言:在四边形ABCD中,∵AB∥CD,AB=CD,∴四边形ABCD是平行四边形.
证明:∵四边形AEFD和EBCF都是平行四边形,∴AD∥ EF,AD=EF, EF∥ BC, EF=BC.∴AD∥ BC,AD=BC.∴四边形ABCD是平行四边形.
四边形AEFD和EBCF都是平行四边形,求证:四边形ABCD 是平行四边形.
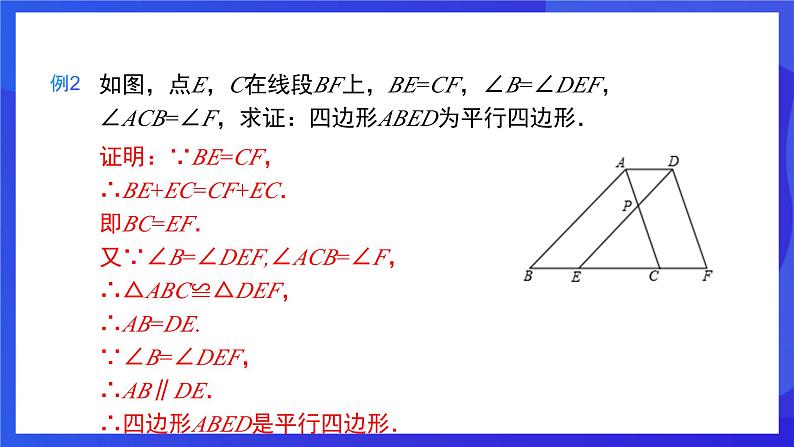
如图,点E,C在线段BF上,BE=CF,∠B=∠DEF,∠ACB=∠F,求证:四边形ABED为平行四边形.
证明:∵BE=CF,∴BE+EC=CF+EC.即BC=EF.又∵∠B=∠DEF,∠ACB=∠F,∴△ABC≌△DEF,∴AB=DE.∵∠B=∠DEF,∴AB∥DE.∴四边形ABED是平行四边形.
在四边形 ABCD 中 , 已知 AD ∥ BC, 若再添加一个条件 , 能使四边形 ABCD 成为平行四边形 , 则这个条件可以 是_________________
( 写出一个条件即可 , 不再添加辅助线 ) .
分析 平行添加条件 AD = BC, 可得出该四边形是平行四边形 .∵ AD ∥ BC, AD = BC, ∴ 四边形 ABCD 是平行四边形 ( 一组对边平行且相等的四边形是平行四边形 ) .
AD = BC ( 答案不唯一 )
解 四边形 BCFD 是平行四边形 .
证明:因为 E 是 CD 的中点 , 所以 DE = CE.
又因为 AD ∥ BC, 点 F 在 AD 的延长线上 ,
所以 ∠ DFE =∠ CBE, ∠ FDE =∠ BCE.
在 △ FDE 与 △ BCE 中 ,
∵ ∠ DFE =∠ CBE, ∠ FDE =∠ BCE, DE = CE,
所以 △ FDE ≌ △ BCE ( AAS ) , 所以 DF = BC.
又因为 DF ∥ BC, 所以四边形 BCFD 是平行四边形 .
解 (1) 证明: ∵ BE = FC, ∴ BC = FE.
在 △ ABC 和 △ DFE 中 ,
∵ AB = DF, AC = DE, BC = FE,
∴△ ABC ≌ △ DFE (SSS) .
(2) 由 (1) 知 △ ABC ≌ △ DFE,
∴∠ ABC =∠ DFE, ∴ AB ∥ DF.
又 ∵ AB = DF, ∴ 四边形 ABDF 是平行四边形 .
解 (1) 证明: ∵ AC ⊥ BD, ∠ FCA = 90 ° , ∴ BD ∥ CF. ∵∠ CBF =∠ DCB, ∴ CD ∥ BF, ∴ 四边形 DBFC 是平行四边形 .
解 ∵ AD ∥ BC, ∴ AP ∥ BQ.
只有当 AP = BQ 时 , 四边形 ABQP 是平行四边形 .
设 t 秒后四边形 ABQP 是平行四边形 ,
此时 , AP = t, BQ = 6 - 2 t,
∴ t = 6 - 2 t, 解得 t = 2 .
即 2 s 后四边形 ABQP 是平行四边形 .
平行四边形的判定(2)
平行四边形的性质与判定的综合运用
1.已知四边形ABCD中有四个条件:AB∥CD,AB=CD,BC∥AD,BC=AD,从中任选两个,不能使四边形ABCD成为平行四边形的选法是 ( )A.AB∥CD,AB=CDB.AB∥CD,BC∥AD C.AB∥CD,BC=AD D.AB=CD,BC=AD
2.四边形ABCD中,对角线AC、BD相交于点O,给出下列四个条件:①AD∥BC;②AD=BC;③OA=OC;④OB=OD.从中任选两个条件,能使四边形ABCD为平行四边形的选法有( )A.3种 B.4种 C.5种 D.6种
3.在▱ABCD中,E、F分别在BC、AD上,若想要使四边形AFCE为平行四边形,需添加一个条件,这个条件不可以是 ( )A.AF=CE B.AE=CF C.∠BAE=∠FCD D.∠BEA=∠FCE
4. 已知四边形ABCD中,AB∥CD,AB=CD,周长为20cm,两邻边的比是3:2,则较大边的长度是( ) A.4cm B.5cm C.6cm D.7cm
5.如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,AE=DF,∠A=∠D,AB=DC.求证:四边形BFCE是平行四边形.
证明:∵AB=CD,∴AB+BC=CD+BC,即AC=BD,在△ACE和△DBF中, AC=BD ,∠A=∠D, AE=DF ,∴△ACE≌△DBF(SAS),∴CE=BF,∠ACE=∠DBF,∴CE∥BF,∴四边形BFCE是平行四边形.
证明: ∵四边形ABCD是平行四边形,∴AB =CD,EB //FD.又∵EB = AB ,FD = CD,∴EB =FD .∴四边形EBFD是平行四边形.
6.如图 ,在平行四边形ABCD中,E,F分别是AB,CD的中点.求证:四边形EBFD是平行四边形.
相关课件
这是一份人教版(2024)八年级下册20.2 数据的波动程度优秀课件ppt,文件包含人教版数学八年级下册2021《方差》同步课件pptx、人教版数学八年级下册2021《方差》分层练习原卷版docx、人教版数学八年级下册2021《方差》分层练习解析版docx等3份课件配套教学资源,其中PPT共21页, 欢迎下载使用。
这是一份人教版(2024)八年级下册19.1 变量与函数优秀课件ppt,文件包含人教版数学八年级下册19112《函数》同步课件pptx、人教版数学八年级下册19112《函数》分层练习原卷版docx、人教版数学八年级下册19112《函数》分层练习解析版docx等3份课件配套教学资源,其中PPT共28页, 欢迎下载使用。
这是一份初中数学18.1.2 平行四边形的判定优质ppt课件,文件包含人教版数学八年级下册18121《平行四边形的判定》第1课时同步课件pptx、人教版数学八年级下册18121《平行四边形的判定》第1课时分层练习解析版docx、人教版数学八年级下册18121《平行四边形的判定》第1课时分层练习原卷版docx等3份课件配套教学资源,其中PPT共25页, 欢迎下载使用。









