沪教版（五四制）（2024）八年级上册17．1 一元二次方程的概念一等奖教学课件ppt

这是一份沪教版（五四制）（2024）八年级上册17．1 一元二次方程的概念一等奖教学课件ppt，共30页。PPT课件主要包含了学习目标，引入新课，新课讲解，课本例题，3方程的根，知识拓展，课本练习，新知讲授，随堂检测，课堂小结等内容，欢迎下载使用。
1.掌握一元二次方程的概念；2、掌握一元二次方程的一般形式，各项及各项的系数；3、学会判断一个数是不是一元二次方程的根；
印度古算书有这样一首诗“一群猴子分两队，高高兴兴在游戏，八分之一再平方，蹦蹦跳跳树林里；其余十二叽喳喳，伶俐活泼又调皮。告我总数共多少，两队猴子在一起。”
一块长方形绿地的面积为1200平方米，并且长比宽多10米，那么长和宽各为多少米？
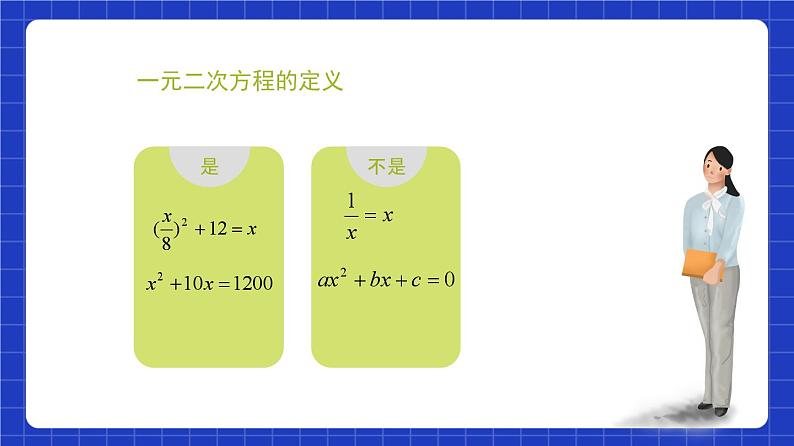
只含有一个未知数，并且未知数的最高次数是二次
1.一元二次方程的概念
只含有一个未知数，并且未知数的最高次数是2的整式方程叫做一元二次方程．
判断下列方程哪些是一元二次方程：
2.一元二次方程的一般形式：
一般地,任何一个关于x 的一元二次方程都可以化为 ax2＋bx+c=0( a≠0 )的形式。
当 a ≠ 0 ， b = 0时
当 a ≠ 0 ， c = 0时
ax2＋bx = 0
当 a ≠ 0 ，b = c =0时
总结：若ax2+bx+c=0是一元二次方程只要满足a ≠ 0 ，b ， c 可以为任意实数.
为什么一般形式ax2+bx+c=0中要限制a≠0，b、c 可以为零呢？
当b ≠ 0时，为一元一次方程
a x 2 + b x + c = 0
指出方程各项的系数时要带上前面的符号哟.
二次项、二次项系数；一次项、一次项系数；常数项：
能够使方程左右两边的值相等的未知数的值叫做方程的解。
只含有一个未知数的方程，它的解又叫做方程的根。
方程有一个根为0：（1）、（2）
（1）2x2＋x=0； （2）5x2－4x=0；（3）3x2＋2x－5=0； （4）x2－7x＋6=0； （5）x2＋5x＋4=0； （6）2x2－3x－5=0. 　　
在下列方程中，哪些方程有一个根为0？
（1）2x2＋x=0； （2）5x2－4x=0；（3）3x2＋2x－5=0； （4）x2－7x＋6=0； （5）x2＋5x＋4=0； （6）2x2－3x－5=0. 　　
在下列方程中,哪些方程有一个根为1？ 哪些方程有一个根为－1？
方程有一个根为1：（3）、（4）
方程有一个根为-1: （5）、（6）
聪明的你能编几个一元二次 方程，使它们有一个根为0，或为1，为-1吗？
1.判断下列方程，哪些是一元二次方程？
两个未知数，二元的方程
练习1判断下列方程，哪些是一元二次方程？
判断一个方程是不是一元二次方程
2.如果方程(m－3)xm2－7－x ＋3＝0是关于x一元二次方程，那么m的值为(　　)A．±3　 B．3 C．－3　 D．以上都不对
3. 一元二次方程3x2=5x的二次项系数和一次项系数分别 是（ ） A. 3，5 B. 3，0 C. 3，-5 D. 5，0
4. 下列哪些数是方程x2+x-12=0的根？ －4， －3， －2， －1， 0， 1， 2， 3， 4.
5.将方程3x(x－1)＝5(x＋2)化成一元二次方程的一般形式，并 写出其中的二次项系数、一次项系数和常数项．
去括号，得3x2－3x＝5x＋10.移项，合并同类项，得一元二次方程的一般形式3x2－8x－10＝0.
所以二次项系数为3，一次项系数为－8，常数项为－10.
6. 根据下列问题列方程，并将其化成一元二次方程的一般形式. 有一根1 m长的铁丝，怎样用它围一个面积为0.06 m2的平 方的长方形?
解：设长方形的长为x m，则宽为(0.5-x)m. 根据题意，得x(0.5-x)=0.06. 整理，得50x2-25x+3=0.
7.已知a是方程 x2+2x-2=0 的一个实数根，求 3a2+6a+ 2 019的值.
由题意，得a2+2a-2=0，即a2+2a=2.
∴ 3a2+6a+2 019=3(a2+2a)=3×2 +2 019=2 025.
已知方程的解求代数式的值，一般先把已知解代入方程，得到等式，将所求代数式的一部分看作一个整体，再用整体思想代入求值．
ax2+bx+c=0(a≠0)