沪教版（五四制）数学八年级上册第17章《一元二次方程》（单元复习课件）

这是一份沪教版（五四制）数学八年级上册第17章《一元二次方程》（单元复习课件），共33页。
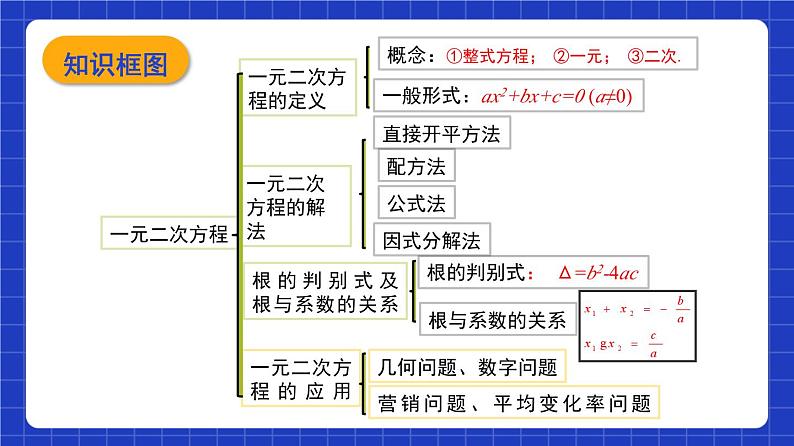
第 17 章一元二次方程单元复习沪教版（五四制）数学八年级上册1.梳理本章的知识结构网络，回顾与复习本章知识.2.能选择适当的方法，快速、准确地解一元二次方程，知道一元二次方程根的判别式和一元二次方程根与系数的关系，并能利用它们解决有关问题.3.列一元二次方程解决实际问题.（重、难点）4.进一步加深对方程思想、分类思想、转化思想（即降次）的理解与运用.学习目标一元二次方程一元二次方程的定义概念：①整式方程； ②一元； ③二次.一般形式：ax2+bx+c=0 (a≠0)一元二次方程的解法直接开平方法配方法公式法因式分解法根的判别式及根与系数的关系根的判别式： Δ=b2-4ac根与系数的关系一元二次方程的应用营销问题、平均变化率问题几何问题、数字问题知识框图考点01一元二次方程的基本概念1.定义：只含有一个未知数的整式方程，并且都可以化为 ax2＋bx＋c＝0(a，b，c为常数，a≠0)的形式，这样的方程叫做一元二次方程．2.一般形式：ax2 ＋ bx ＋c＝0 (a，b，c为常数，a≠0)1个概念 3.项数和系数： ax2 ＋ bx ＋c＝0 (a，b，c为常数，a≠0) 二次项： ax2 二次项系数：a 一次项：bx 一次项系数：b 常数项：c4.注意事项： (1)含有一个未知数； (2)未知数的最高次数为2； (3)二次项系数不为0； (4)整式方程． 【例1】若关于x的方程(m-1)x2+mx-1=0是一元二次方程，则m的取值范围是（ ） A. m≠1 B. m=1 C. m≥1 D. m≠0解析 本题考查了一元二次方程的定义，即方程中必须保证有二次项（二次项系数不为0），因此它的系数m-1≠0,即m≠1,故选A.A【变式】方程5x2-x-3=x2-3+x的二次项系数是 ，一次项系数是 ，常数项是 .4-20考点02一元二次方程的解法x2 + px + q = 0 （p2 - 4q ≥0）(x+m)2＝n（n ≥ 0）ax2 + bx +c = 0(a≠0 , b2 - 4ac≥0)(x + m) （x + n）＝0各种一元二次方程的解法及使用类型1个解法【易错提示】(1)配方法的前提是二次项系数是1；（a-b)2与（a+b)2 要准确区分；（2）求三角形的周长，不能盲目地将三边长相加起来，而应养成检验三边长能否成三角形的好习惯解析 (1)配方法的关键是配上一次项系数一半的平方； （2）先求出方程x2﹣13x+36=0的两根，再根据三角形的三边关系定理，得到符合题意的边，进而求得三角形周长．例2 (1)用配方法解方程x2-2x-5=0时，原方程应变为（ ） A. (x-1)2=6 B.(x+2)2=9 C. (x+1)2=6 D.(x-2)2=9 (2) (易错题）三角形两边长分别为3和6，第三边的长是方程x2﹣13x+36=0的根，则该三角形的周长为（　）　A．13 B． 15 C．18 D．13或18AA【变式1】菱形ABCD的一条对角线长为6，边AB的长是方程x2-7x+12=0的一个根，则菱形ABCD的周长为（ ） A. 16 B. 12 C. 16或12 D. 24A【变式2】用适当的方法解下列方程．(1)2(x－1)2－4＝0；10(2)x(x－2)＋x－2＝0；解：原方程可化为(x－2)(x＋1)＝0，解得x1＝2，x2＝－1.(3)(x－2)(x＋3)＝66.解：原方程化为一般形式为x2＋x－72＝0.分解因式，得(x＋9)(x－8)＝0，解得x1＝－9，x2＝8.当m为何值时，方程 （1）有两个相等实根；（2）有两个不等实根；（3）有实根；（4）无实数根；（5）只有一个实数根；（6）有两个实数根。m-1≠0且Δ=0m-1≠0且Δ＞0△≥0或者m-1=0△＜0且m-1≠0m-1=0△≥0且m-1≠02个关系考点03 一元二次方程根的判别式A易错提示 应用根的判别式之前务必将方程化为一般形式，这样能帮助我们正确确定a,b,c的值.【变式1】下列所给方程中，没有实数根的是（ ）A. x2+x=0 B. 5x2-4x-1=0 C.3x2-4x+1=0 D. 4x2-5x+2=0【变式2】（开放题）若关于x的一元二次方程x2-x+m=0有两个不相等的实数根，则m的值可能是　　（写出一个即可）．D0【变式3】已知关于x的方程x2＋mx＋m－2＝0.(1)若此方程的一个根为1，求m的值；(2)求证：不论m取何实数，此方程都有两个不相等的实数根．16考点04 根与系数的关系1个应用考点05 一元二次方程的实际应用【例5】某工厂一种产品2018年的产量是300万件，计划2020年的产量达到363万件．假设2018年到2020年这种产品产量的年增长率相同．(1)求2018年到2020年这种产品产量的年增长率；(2)2019年这种产品的产量为多少万件？解：(1)设2018年到2020年这种产品产量的年增长率为x.由题意，得300(1＋x)2＝363，解得x1＝0.1＝10%，x2＝－2.1(舍去)．故2018年到2020年这种产品产量的年增长率为10%.　(2)300×(1＋10%)＝330(万件)，故2019年这种产品的产量为330万件． 【变式1】某机械公司经销一种零件，已知这种零件的成本为每件20元，调查发现当销售价为24元，平均每天能售出32件，而当销售价每上涨2元，平均每天就少售出4件. (1)若公司每天的销售价为x元，则每天的销售量为多少？（2）如果物价部门规定这种零件的销售价不得高于每件28元，该公司想要每天获得150元的销售利润，销售价应当为多少元？市场销售问题解析 本题为销售中的利润问题，其基本本数量关系用表析分如下：设公司每天的销售价为x元.432x-2032-2(x-24)150其等量关系是：总利润=单件利润×销售量.解：（1）32-(x-24) ×2=80-2x;（2）由题意可得(x-20)(80-2x)=150.解得 x1=25, x2=35.由题意x≤28, ∴x=25,即售价应当为25元.【易错提示】销售量在正常销售的基础上进行减少.要注意验根.128【变式2】菜农小王种植的某种蔬菜，计划以每千克5元的价格对外批发销售.由于部分菜农盲目扩大种植，造成该种蔬菜滞销.小王为了加快销售，减少损失，对价格经过两次下调后，以每千克3.2元的价格对外批发销售.求平均每次下调的百分率是多少？解：设平均每次下调的百分率是x，根据题意得 5（1-x)2=3.2 解得 x1=1.8 (舍去）, x2=0.2=20%.答：平均每次下调的百分率是20%.平均变化率问题 【变式3】如图1，在宽为20米，长为32米的矩形地面上修筑同样宽的道路（图中阴影部分），余下的部分种上草坪．要使草坪的面积为540平方米，求道路的宽. 解析 本题利用图形的变换——平移，把零散的图形面积集中化，再建立方程并求解.几何问题解：设道路宽为x米，由平移得到图2，则宽为(20-x)米，长为（32-x)米，列方程得（20-x)(32-x)=540，整理得 x2-52x+100=0.解得 x1=50(舍去），x2=2.答：道路宽为2米. 解决有关面积问题时，除了对所学图形面积公式熟悉外，还要会将不规则图形分割或组合成规则图形，并找出各部分图形面积之间的关系，再列方程求解.（注意：这里的横坚斜小路的的宽度都相等）平移转化方法总结【变式4】(易错题）要在一块长52米，宽48米的矩形绿地上，修建同样宽的两条互相垂直的甬路，下面分别是小亮和小颖的设计方案.小亮设计的方案如图①所示，甬面宽度均为xm,剩下四块绿地面种共2300m2.小颖设计的方案如图②所示，BC=HE=xm,AB∥CD,HG∥EF,AB ⊥EF, ∠1=60 °.解:(1)根据小亮的设计方案列方程，得（52-x)(48-x)=2300.解得x1=2,x2=98(不合题意，舍去）.答：小亮设计方案中甬路的宽度为2m；(2)在图2中作AI⊥CD,HJ⊥EF,垂足分别是为I,J.∵AB ∥CD, ∴四边形ADCB是平行四边形.由（1）得x=2, ∴AD=BC=HE=2m.在Rt △ADI中， ∠ADC=∠1=60 °，AD=2m,∴AI= m,同理HJ= m.∴小颖设计方案中四块绿地的总面积=52 ×48-2 ×52-2×48+ =2299（m2).JI1．已知关于x的方程(a－3)x|a－1|＋x－1＝0是一元二次方程，则a的值是(　　)A．－1 B．2C．－1或3 D．32．已知关于x的一元二次方程(k＋1)x2＋2x＋k2－2k－3＝0的常数项等于0，则k的值等于(　　)A．－1 B．3C．－1或3 D．－3A B 易错集训3．方程(3x－4)2＝3x－4的根是______________________.4．如果关于x的一元二次方程(k＋2)x2－3x＋1＝0有实数根，那么k的取值范围是____________________.5．已知关于x的一元二次方程x2－6x＋n－1＝0有实数根．(1)求n的取值范围；(2)若等腰三角形边长分别为a，b,2，且a，b是方程的两根，求n的值和三角形的周长．解：(1)依题意，得Δ＝(－6)2－4(n－1)≥0，即10－n≥0，解得n≤10.　(2)∵三角形是等腰三角形，∴有a＝2或b＝2和a＝b两种情况．①当a＝2或b＝2时，∵a、b是关于x的一元二次方程x2－6x＋n－1＝0的两根，∴x＝2.把x＝2代入x2－6x＋n－1＝0，得22－6×2＋n－1＝0，解得n＝9.当n＝9，方程的两根是2和4，而2、4、2不能组成三角形，故n＝9不合题意；②当a＝b时，方程x2－6x＋n－1＝0有两个相等的实数根，∴Δ＝(－6)2－4(n－1)＝0，解得n＝10.此时方程的解为x1＝x2＝3，即a＝b＝3，则等腰三角形的周长为3＋3＋2＝8.综上所述，n＝10，三角形的周长为8.素养提升根据上面的方法解方程：(x2－x)2－4(x2－x)－12＝0.解：设x2－x＝t，则方程即可变形为t2－4t－12＝(t－6)(t＋2)＝0，解得 t1＝6，t2＝－2.当t＝6时，x2－x＝6，即(x－3)(x＋2)＝0，解得 x＝3或x＝－2；当t＝－2时，x2－x＝－2，即x2－x＋2＝0，∵Δ＝1－8＝－7＜0，∴该方程无实数解，所以原方程有2个根：x1＝3，x2＝－2.7．【江苏徐州中考】如图，有一块矩形硬纸板，长30 cm，宽20 cm.在其四角各剪去一个同样的正方形，然后将四周突出部分折起，可制成一个无盖长方体盒子．当剪去正方形的边长取何值时，所得长方体盒子的侧面积为200 cm2课堂小结课程结束