初中数学沪教版（五四制）（2024）八年级上册19．2 证明举例获奖教学ppt课件

这是一份初中数学沪教版（五四制）（2024）八年级上册19．2 证明举例获奖教学ppt课件，共17页。PPT课件主要包含了学习目标，课本练习，随堂检测，课堂小结等内容，欢迎下载使用。
1．通过证明举例的学习和实践，懂得演绎推理的一般规则，初步掌握规范的表达格式；了解证明之前进行分析的基本思路；2．能利用全等三角形的判定与性质、等腰三角形的性质来证明有关线段相等、角相等的简单问题；3．知道添置辅助线的基本方法，会添置常见的辅助线。
“中线加角平分线问题”是结论不成立呢还是我们不能用上面的方法证明这个问题，这就是我们今天要探究的课题。
提问:（1）等腰三角形有那些性质?（2）根据图形请用几何语言表述等腰三角形三线合一性质（3）若把等腰三角形的三线合一这一性质中的任意两个结论反过来作为条件能不能得到等腰三角形？（4）在学生顺利利用三角形全等证明垂线加中线,垂线加角平分线2个问题后提出问题：能不能用上面直接全等的方法证明中线加角平分线问题，
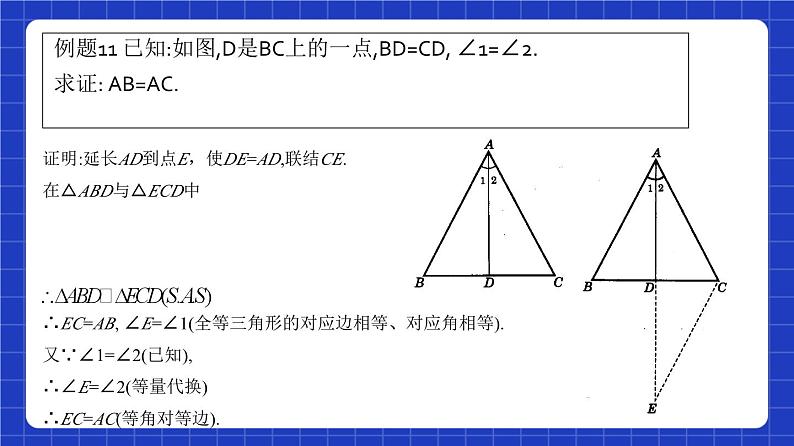
例题11 已知:如图,D是BC上的一点,BD=CD, ∠1=∠2.求证: AB=AC.
证明:延长AD到点E，使DE=AD,联结CE.在△ABD与△ECD中
∴EC=AB, ∠E=∠1(全等三角形的对应边相等、对应角相等).又∵∠1=∠2(已知),∴∠E=∠2(等量代换)∴EC=AC(等角对等边).
本题是证明两条线段相等，图形看似简单，但无法直接运用全等三角形的判定和性质来进行证明.考虑到已知条件中其实有△ACD的中线AD，这为图形的旋转提供了条件.通过倍长中线AD，可作出△ABD关于点D对称的图形.这种添辅助线的方法，在证明直角三角形斜边上的中线的定理时也要用到，本例是一个铺垫。
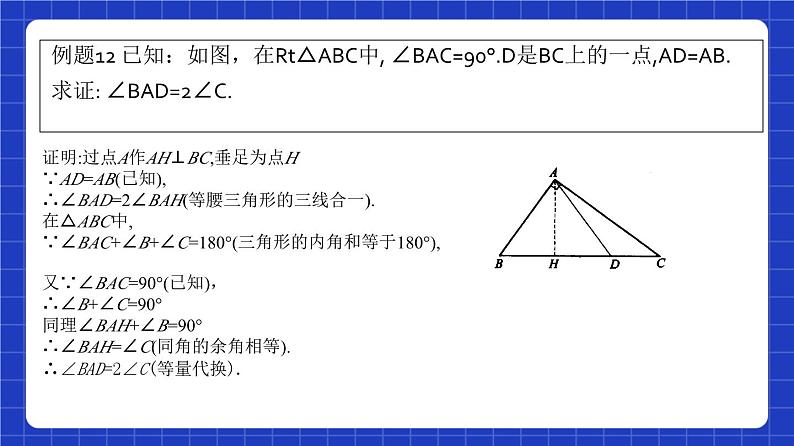
例题12 已知：如图，在Rt△ABC中, ∠BAC=90°.D是BC上的一点,AD=AB.求证: ∠BAD=2∠C.
证明:过点A作AH⊥BC,垂足为点H∵AD=AB(已知),∴∠BAD=2∠BAH(等腰三角形的三线合一).在△ABC中,∵∠BAC+∠B+∠C=180°(三角形的内角和等于180°),
又∵∠BAC=90°(已知)，∴∠B+∠C=90°同理∠BAH+∠B=90°∴∠BAH=∠C(同角的余角相等).∴∠BAD=2∠C(等量代换).
本例要证明两角之间的倍半关系，利用了等腰三角形的三线合一这个基本图形，转化为证两角相等，而证两角相等利用了“同角的余角相等”.以前证明两个角相等，主要考虑利用全等三角形的性质，本例有助于学生拓宽思路．
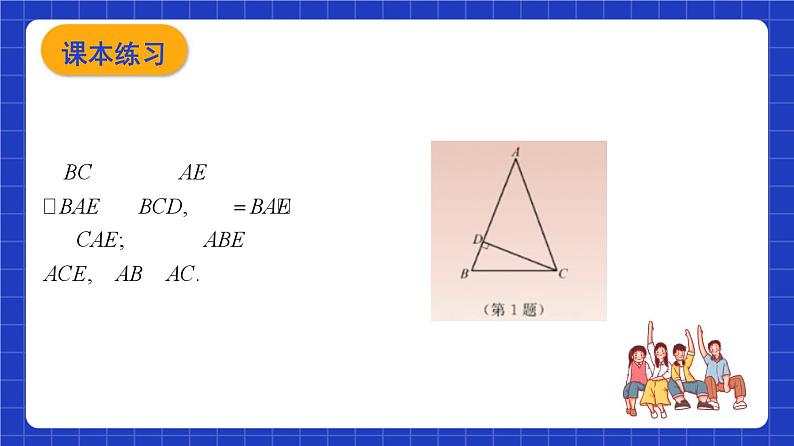
1.如图,在△ABC中,∠1=∠2,∠B=2∠C.求证:AC=AB+BD.
∴△ABD≌△AED(SAS),∴BD=ED,∠B=∠AED.∵∠B=2∠C,∴∠AED=2∠C.又∵∠AED=∠C+∠CDE,∴∠C=∠CDE,∴CE=DE,∴BD=CE.∴AC=AE+CE=AB+BD.
证明:在边AC上截取AE,使AE=AB,连接DE.
2.已知：如图，AD∥BC，点E是DC的中 点，AE平分∠BAD. 求证：BE平分∠ABC.
3.已知：如图，在△ABC中，CD是△ABC角平分线，BC=AC+AD. 求证：∠A=2∠B.
4.如图,在四边形ABDE中,C是BD边的中点.若AC平分∠BAE,∠ACE=90°,猜想线段AE,AB,DE的长度满足的数量关系并证明.
∴△ACB≌△ACF(SAS),∴BC=FC,∠ACB=∠ACF.∵C是BD边的中点.∴BC=CD,∴CF=CD.
解:AE=AB+DE.理由:在AE上取一点F,使AF=AB,连接CF.∵AC平分∠BAE,∴∠BAC=∠FAC.
∵∠ACE=90°,∴∠ACB+∠DCE=90°,∠ACF+∠ECF=90°,∴∠ECF=∠ECD.
∴△CEF≌△CED(SAS),∴EF=ED.∵AE=AF+EF,∴AE=AB+DE.
5.如图,△AOB中,OA=OB,∠AOB=90°,BD平分∠ABO交OA于点D,AE⊥BD于点E.求证:BD=2AE.
∴△OBD≌△OAF(ASA),∴BD=AF.∵AE=EF,∴BD=2AE.
∵BD平分∠ABO,AF⊥BD,∴∠1=∠2,∠AEB=∠FEB=90°,∴易证△ABE≌△FBE(ASA),∴AE=EF.∵∠AOB=90°,∠AED=90°,∠ADE=∠BDO,∴∠2=∠OAF.
证明:延长BO,AE交于点F.
在几何解题中,常常需要添加辅助线构造全等三角形,以沟通条件与结论之间的联系.构造全等三角形,添加辅助线常见类型有以下几种:(1)直接连线构造全等三角形;(2)倍长中线构造全等三角形;(3)作垂线段构造全等三角形;(4)截取法构造全等三角形;(5)延长法构造全等三角形.添加辅助线时要结合已知条件和图形,将已知条件转化到两个三角形中,根据全等三角形判定的方法,能证明两个三角形全等,真正起到“牵线搭桥”的作用.