初中数学沪教版（五四制）（2024）八年级上册19．2 证明举例评优课教学课件ppt

这是一份初中数学沪教版（五四制）（2024）八年级上册19．2 证明举例评优课教学课件ppt，共26页。PPT课件主要包含了学习目标，基本图形，例题8已知如图在，课本练习，随堂检测等内容，欢迎下载使用。
1．通过证明举例的学习和实践，懂得演绎推理的一般规则，初步掌握规范的表达格式；了解证明之前进行分析的基本思路；2．了解证明两线垂直的基本方法，会证明垂直的简单问题；
在同一平面内，两条不重合的直线具有怎样的位置关系？在前几节课我们共同探究了证明两条直线平行的方法，接下来大家认为今天这节课，应该学习哪一类证明呢？为什么？为什么学习了证明平行后就学习证明相交的特例——垂直？价值何在？现在让我们一起来探究证明两条直线垂直的方法．
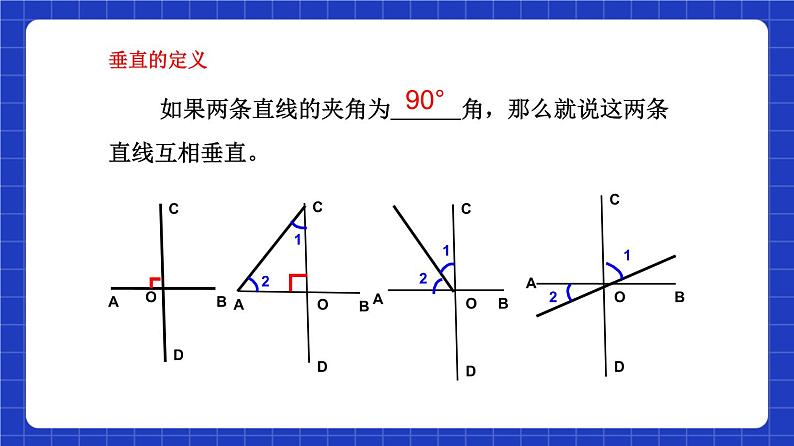
如果两条直线的夹角为     角，那么就说这两条直线互相垂直。
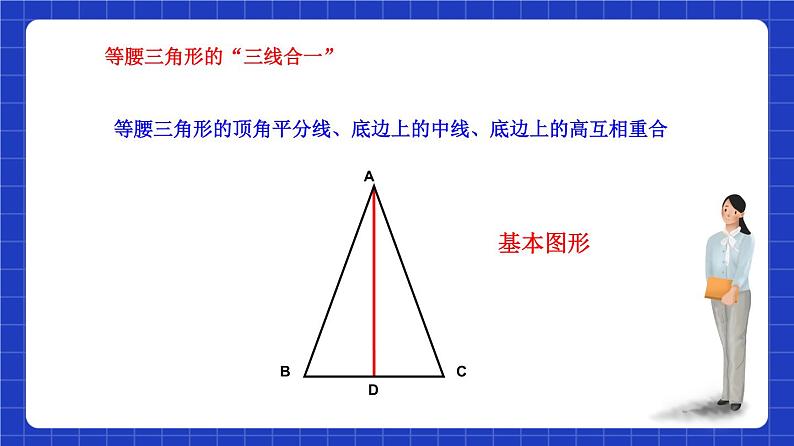
等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合
等腰三角形的“三线合一”
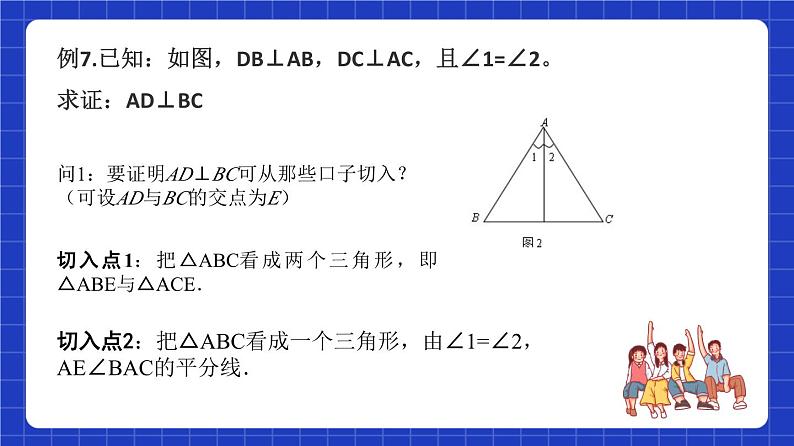
问1：要证明AD⊥BC可从那些口子切入？（可设AD与BC的交点为E）
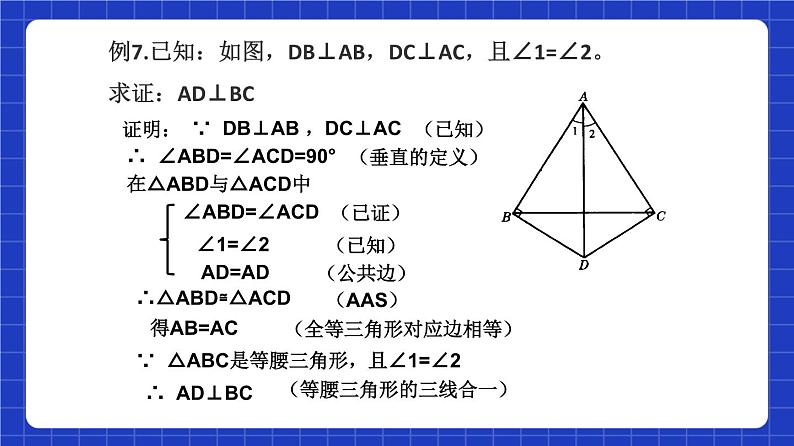
例7.已知：如图，DB⊥AB，DC⊥AC，且∠1=∠2。求证：AD⊥BC
切入点1：把△ABC看成两个三角形，即△ABE与△ACE．
切入点2：把△ABC看成一个三角形，由∠1=∠2，AE∠BAC的平分线．
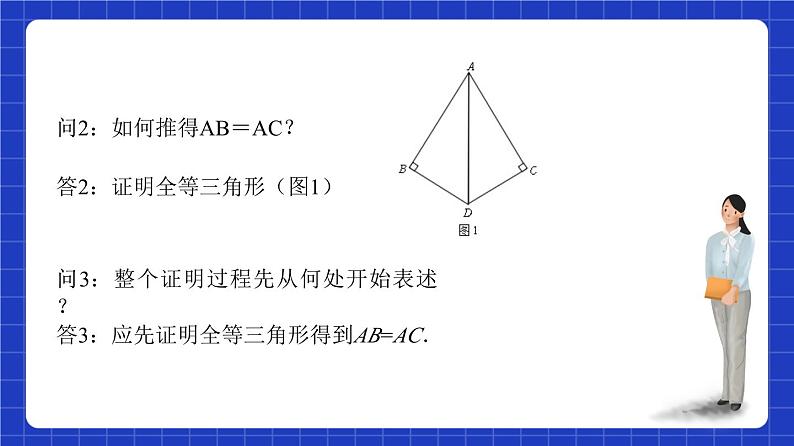
问2：如何推得AB＝AC？
答2：证明全等三角形（图1）
问3：整个证明过程先从何处开始表述？
答3：应先证明全等三角形得到AB=AC．
∵ DB⊥AB ，DC⊥AC
∴ ∠ABD=∠ACD=90°
在△ABD与△ACD中
（全等三角形对应边相等）
∵ △ABC是等腰三角形，且∠1=∠2
（等腰三角形的三线合一）
点E在AC上,且CE=CD.联结BE并延长交AD于点F.求证:BF⊥AD.
中,AC⊥BD,垂足为点C，AC=BC.
分析：问1：要证明BF⊥AD.的关键是什么？
答1：证明∠BFD＝90°（或∠BFA＝90°）
问2如何证明∠BFD＝90°呢？在含∠BFD的△BFD中只要推得∠1＋∠B＝90°就行，而△ACD中，∠ACD＝90°，∠D是与△BFD的公共角，如能推得∠2＝∠1，那么如何推得∠2＝∠1呢
答2：证明△BCE≌△ACD
问3：如果走要证∠BFA＝90°这条路，该在哪两个三角形中来考虑问题比较方便呢？为什么？ 
答3：在△BCE和△AFE中考虑，因为已有∠BCE＝90°，∠3＝∠4，只要推得∠2＝∠1，就可推出∠BFA＝90°
问4：两种思路共同的关键是什么？
答4：共同的关键是证明△BCE≌△AFE，从而推出∠1＝∠2．
变式1：如图：点A、E在CB同侧，且AC⊥CB，EB⊥CB，D为CB上的一点，且AC=BD，CD=BE．求证：AD⊥DE．
∵ AC⊥CB ，EB⊥CB
∴ ∠ACD=∠EBD=90°
在△ACD与△DBE中
（全等三角形对应角相等）
∵ ∠ADE+∠EDB=∠CAD+∠ACD
变式2：如图：点A、E在CB同侧，且AC⊥CB，EB⊥CB，D为CB上的一点，且AC=BC，CD=BE．求证：AD⊥CE．
变式3：如图，在△ABC中，AD=BD=CD，求证：AC⊥BC
如果三角形一边上的中线等于这边的一半, 那么这个三角形是直角三角形
∵ AD=BD=CD
∴ ∠DAC=∠DCA
∠DCB=∠DBC
∵∠DAC+∠DCA+∠DCB+∠DBC=180°
∴2∠DCA+2∠DCB=180°
∴∠DCA+∠DCB=90°
即∠ACB=90°
1.已知：如图，AB=AC，BE=CF，且AB⊥BE，AC⊥CF，点D在EF上，∠BAD=∠CAD．求证：AD⊥EF．
分析：分别联结AE、AF，构造全等三角形，得到等腰三角形．
证明：联结AE、AF. ∵AB⊥BE，AC⊥CF(已知), ∴∠B=∠C=90°(垂直的定义). 在△OAC与△OBD中,
AB=AC (已知), ∠B=∠C (已证), BE=CF (已知), ∴△ABE≌△ACF(S.A.S ). ∴AE=AF (全等三角形的对应边相等 ). ∠1=∠2 (全等三角形的对应角相等 ).又∵∠BAD=∠CAD(已知), ∴∠3=∠4(等式性质). ∵△OCD是等腰三角形,且∠3=∠4, ∴OM⊥CD(等腰三角形的三线合一 ).
2.小明用如下两种方法画出了互相垂直的两条直线，你能证明这两种画法的正确性吗?画法一:
（1） 画∠AOB;（2）以点 O为圆心、任意长为半径画弧,分别交 OA 于点 C，交 OB 于点 D;
（4）分别画射线 OP、线段 CD .则 CD与 OP 互相垂直.
（2）分别联结 AC、BC,延长 AC 到点D,使 CD=CA;（3）联结 DB.则 DB与AB 互相垂直.
已知：如图，点 P 是直线 AB 上一点，求作直线 CD，使 CD⊥AB 于点 P．
2.尺规作图:经过已知直线上的一点作这条直线的垂线.
答：他们的判断是对的．因为等腰三角形底边上的中线和底边上的高重合．
3.某地地震过后,河沿村中学的同学用下面的方法检测教室的房 梁是否水平： 在等腰直角三角尺斜边中点拴一条线绳,线绳的另一端挂一个 铅锤,把这块三角尺的斜边贴在房梁上,结果线绳经过三角尺的 直角项点,同学们由此确信房梁是水平的,他们的判断对吗?为 什么?
4. 已知点D、E在△ABC的边BC上，AB＝AC.(1)如图①，若AD＝AE，求证：BD＝CE；(2)如图②，若BD＝CE，F为DE的中点，求证：AF⊥BC.
证明：(1)如图①，过A作AG⊥BC于G.∵AB＝AC，AD＝AE，∴BG＝CG，DG＝EG，∴BG－DG＝CG－EG，∴BD＝CE；(2)∵BD＝CE，F为DE的中点，∴BD＋DF＝CE＋EF，∴BF＝CF.∵AB＝AC，∴AF⊥BC.