初中数学沪教版（五四制）（2024）八年级上册19．2 证明举例获奖教学课件ppt

这是一份初中数学沪教版（五四制）（2024）八年级上册19．2 证明举例获奖教学课件ppt，共17页。PPT课件主要包含了学习目标，课本练习，随堂检测，课堂小结等内容，欢迎下载使用。
1．通过证明举例的学习和实践，懂得演绎推理的一般规则，初步掌握规范表达的格式；2．了解证明之前进行分析的基本思路；3．能利用全等三角形的判定与性质来证明有关线段相等以及两条直线的平行的简单问题。
方法总结：判定两个三角形全等时找条件的方法
判定两个三角形全等时，如果给出的条件不全，就需要根据已知条件结合相应的判定方法来进行分析，先推导出所缺的条件，然后证明。
（1）已知一边及与其相邻的一个内角分别相等：判定两个三角形全等的方法中边和角相邻的有“SAS”“ASA”“AAS”,所以可以从这三个方面进行考虑。（2）已知两边分别相等：判定两个三角形全等的方法中含有两边的有“SAS”“SSS”，所以可以从这两个方面进行考虑。（3）已知两角分别相等：判定两个三角形全等的方法中含有两角的有“AAS”“ASA”，所以可以从这两个方面进行考虑。（4）已知一边与其对角分别相等，与之相对应的判定方法只有“AAS”，可以考虑首先得出这条边的某一邻角也相等，然后判定两个三角形全等。
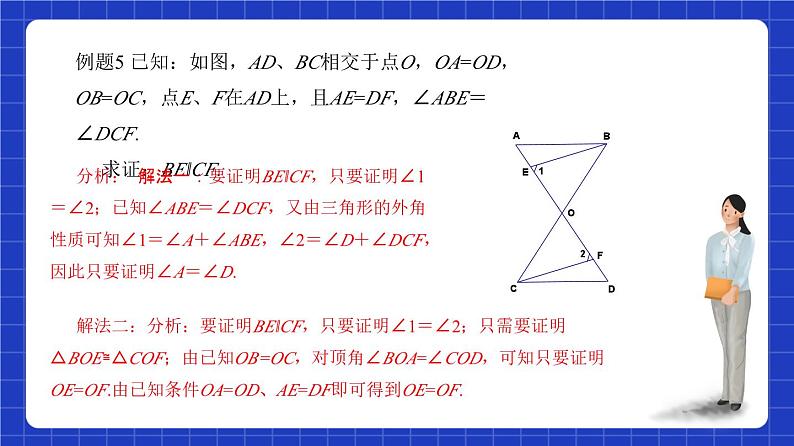
例题5 已知：如图，AD、BC相交于点O，OA=OD，OB=OC，点E、F在AD上，且AE=DF，∠ABE＝∠DCF.求证：BE‖CF.
分析： 解法一：要证明BE‖CF，只要证明∠1＝∠2；已知∠ABE＝∠DCF，又由三角形的外角性质可知∠1＝∠A＋∠ABE，∠2＝∠D＋∠DCF，因此只要证明∠A＝∠D.
解法二：分析：要证明BE‖CF，只要证明∠1＝∠2；只需要证明△BOE≌△COF；由已知OB=OC，对顶角∠BOA=∠COD，可知只要证明OE=OF.由已知条件OA=OD、AE=DF即可得到OE=OF.
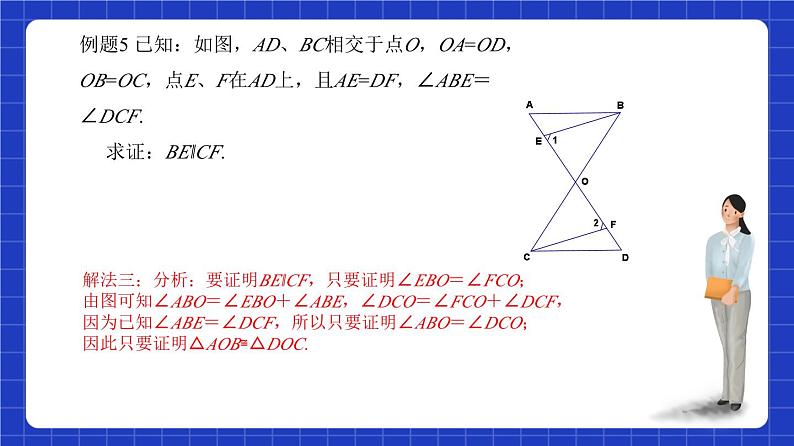
解法三：分析：要证明BE‖CF，只要证明∠EBO＝∠FCO；由图可知∠ABO＝∠EBO＋∠ABE，∠DCO＝∠FCO＋∠DCF，因为已知∠ABE＝∠DCF，所以只要证明∠ABO＝∠DCO；因此只要证明△AOB≌△DOC.
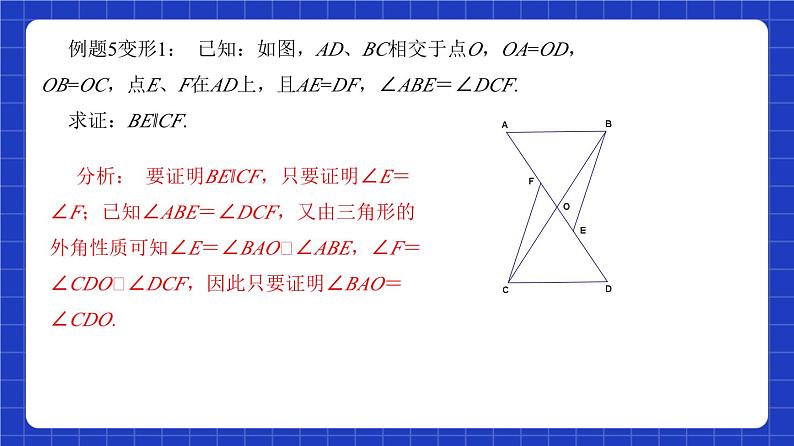
例题5变形1： 已知：如图，AD、BC相交于点O，OA=OD，OB=OC，点E、F在AD上，且AE=DF，∠ABE＝∠DCF.求证：BE‖CF.
分析： 要证明BE‖CF，只要证明∠E＝∠F；已知∠ABE＝∠DCF，又由三角形的外角性质可知∠E＝∠BAO﹣∠ABE，∠F＝∠CDO﹣∠DCF，因此只要证明∠BAO＝∠CDO.
例题5变形2： 已知：如图，AD、BC相交于点O，OA=OD，OB=OC，点E、F在AD上，且AE=DF，∠ABE＝∠DCF.求证：BE‖CF.
例题6 已知：如图，AD∥BC,E是线段BC的中点，AE=DE.求证：AB=DC.
分析：要证明AB=DC，只需要证明△ABE≌△DCE；由AE=DC，可知∠3＝∠4，又因为AD∥BC，所以得到∠1＝∠2；只要再找出一条边或一个角的情况即可；结合E是线段BC的中点，可知EB=EC，可以证明△ABE≌△DCE.
1.已知:如图,BE⊥AC,DF⊥AC,垂足分别是点 E、F.AF=CE,BE=DF.求证:AB=CD,AB//CD.
2.已知:如图,DE//BC,A 是 DE 上一点,AD=AE,AB=AC.求证;BE=CD.
1.如图，已知△ACE≌△DBF，CE=BF，AE=DF，AD=8，BC=2．（1）求AC的长度；（2）试说明CE∥BF．
解：（1）∵△ACE≌△DBF，∴AC=BD，则AB=DC.∵BC=2，∴2AB+2=8，∴AB=3，∴AC=3+2=5；（2）∵△ACE≌△DBF，∴∠ECA=∠FBD，∴CE∥BF．
解： DE=BF，DE//BF. 在△ADC和△CBA中， CD=AB， DA=BC， AC=CA， ∴ △ADC≌△CBA（SSS）. ∴∠DAC=∠BCA.
2.如图，已知AB=CD，BC=DA，E、F是AC上的两点，且AE=CF，写出DE和BF之间的关系，并证明你的结论.
3．【山西中考】如图，点B、D在线段AE上，AD＝BE，AC∥EF，∠C＝∠F.求证：BC＝DF.
4．【重庆中考】如图，在△ABC中，AB＝AC，AD⊥BC于点D.(1)若∠C＝42°，求∠BAD的度数；(2)若点E在边AB上，EF∥AC交AD的延长线于点F.求证：AE＝FE.(1)解：∵AB＝AC，AD⊥BC，∴∠BAD＝∠CAD，∠ADC＝90°.又∵∠C＝42°，∴∠BAD＝∠CAD＝90°－42°＝48°.　(2)证明：∵AB＝AC，AD⊥BC，∴∠BAD＝∠CAD.∵EF∥AC，∴∠F＝∠CAD，∴∠BAD＝∠F，∴AE＝FE.
１．三角形中，等角对等边证明两条线段相等
２．等量±等量和（差）相等
３．利用全等三角形证明两条线段相等